ONLY use MATLAB please And use the function bin2dec

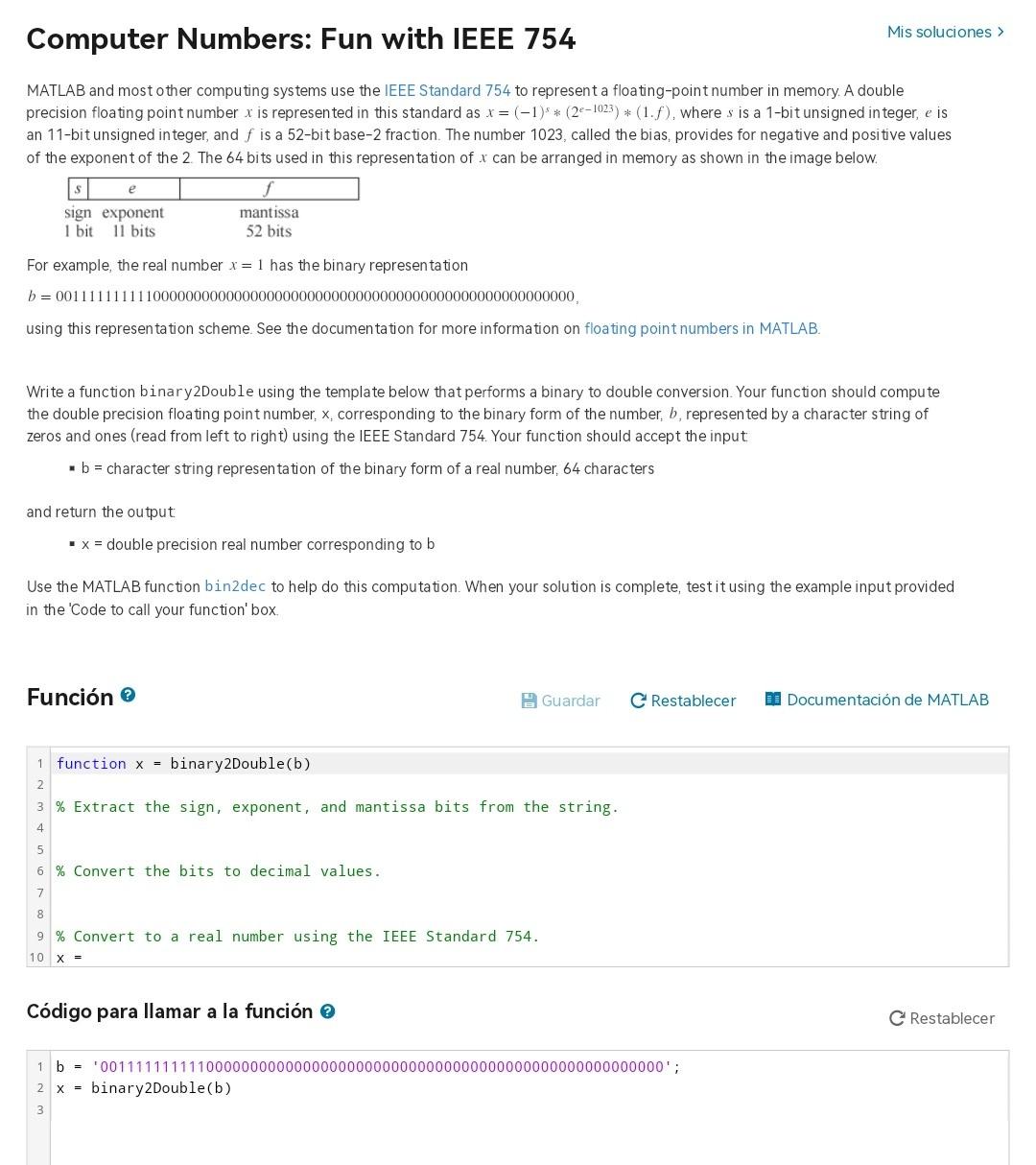
Computer Numbers: Fun with IEEE 754 MATLAB and most other computing systems use the IEEE Standard 754 to represent a floating-point number in memory. A double precision floating point number x is represented in this standard as x=(1)s(2e1023)(1.f), where s is a 1-bit unsigned integer, e is an 11-bit unsigned integer, and f is a 52-bit base-2 fraction. The number 1023 , called the bias, provides for negative and positive values of the exponent of the 2 . The 64 bits used in this representation of x can be arranged in memory as shown in the image below. For example, the real number x=1 has the binary representation b=001111111110000000000000000000000000000000000000000000000000000 using this representation scheme. See the documentation for more information on floating point numbers in MATLAB. Write a function binary2Double using the template below that performs a binary to double conversion. Your function should compute the double precision floating point number, x, corresponding to the binary form of the number, b, represented by a character string of zeros and ones (read from left to right) using the IEEE Standard 754. Your function should accept the input: - b = character string representation of the binary form of a real number, 64 characters and return the output - x= double precision real number corresponding to b Use the MATLAB function bin2dec to help do this computation. When your solution is complete, test it using the example input provided in the 'Code to call your function' box. Funcin 0 \begin{tabular}{|r|l} 1 & function x= binary2Double(b) \\ 2 & \\ 3 & % Extract the sign, exponent, and mantissa bits from the string. \\ 4 & \\ 5 & \\ 6 & % Convert the bits to decimal values. \\ 7 & \\ 8 & \\ 9 & % Convert to a real number using the IEEE Standard 754. \\ 10 & x= \end{tabular} Cdigo para llamar a la funcin 3 Cestablecer 123b=0011111111110000000000000000000000000000000000000000000000000000;x=binary2Double(b)