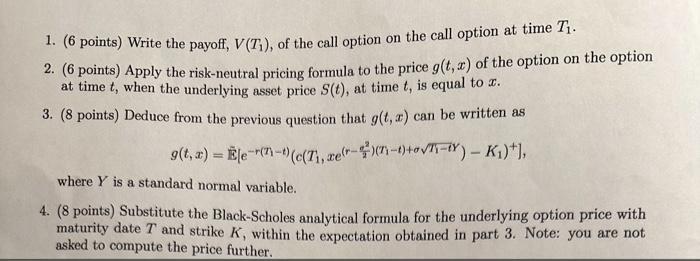
Option pricing We consider a European call option with maturity date T > 0 and strike price K > 0 on a European call option with maturity date T > T and strike price K > 0, on an underlying asset with price process S(t) such that dS(t)=rS(t)dt+oS(t)dw(t), where r > 0, > 0 are constant and is a standard Brownian motion under the risk neutral probability measure. We denote by c(t, s) the price of the underlying call option. It is given explicitly by the Black-Scholes formula with the parameters r, T, K, a. 1. (6 points) Write the payoff, V(T), of the call option on the call option at time T. 2. (6 points) Apply the risk-neutral pricing formula to the price g(t, x) of the option on the option at time t, when the underlying asset price S(t), at time t, is equal to x. 3. (8 points) Deduce from the previous question that g(t, x) can be written as 9(t, c) = [e ++)\(c(Ti,ze--+VI-) Ki)], where Y is a standard normal variable. 4. (8 points) Substitute the Black-Scholes analytical formula for the underlying option price with maturity date T and strike K, within the expectation obtained in part 3. Note: you are not asked to compute the price further.