Overview

For this assignment, you'll implement Kruskal's algorithm on adjacency list representations of undirected, weighted graphs using a disjoint-set data structure. This assignment is a pure programming assignment.

Implementation

Code must be in a file calledkruskals.py. Algorithm must be in a function calledkruskals.

Kruskalsfunction will take two arguments: an adjacency list representation of a undirected, weighted graph and an edge weight dictionary mapping node tuples (edges) to integers (edge weights).

Code should not modify any of the arguments that are passed to it (i.e. it shouldn't mutate the original graph objects).

Function should return the total weight (i.e. the sum of all the edge weights) of a minimum spanning tree in the graph. If the graph has no edges, the total weight of the MST is 0.

Algorithm must use a disjoint-set data structure to check if adding an edge to the current spanning tree will introduce a cycle. You may implement this any way you like (as long as your data structure is fundamentally a disjoint-set), but the most efficient and interesting implementation is with a rooted tree that uses path compression and union by rank.

Graph representation

Graphs will be represented as dictionaries where each key is a node label and each value is a list of labels, representing the node's edges.

For example, the dictionary entry'a': ['b', 'c']means the node with labelahas two edges: one tob, and one toc. Labels may be strings, integers, etc. Because the graph is undirected, if nodeuhas an edge tov, thenvwill be inu's adjacency list anduwill be inv's adjacency list.

Edge weights will be represented as dictionaries where each key is a tuple of node labels and each value is an integer weight. For example, the dictionary entry('c', 'b'): 7means the edge betweenbandchas weight 7.

Each undirected edge will be represented exactly once in the edge weight dictionary, in arbitrary order. For example, ifbhas an edge toc, then the edge weight dictionary will either contain the tuple('b', 'c')or the tuple('c', 'b'), but not both.

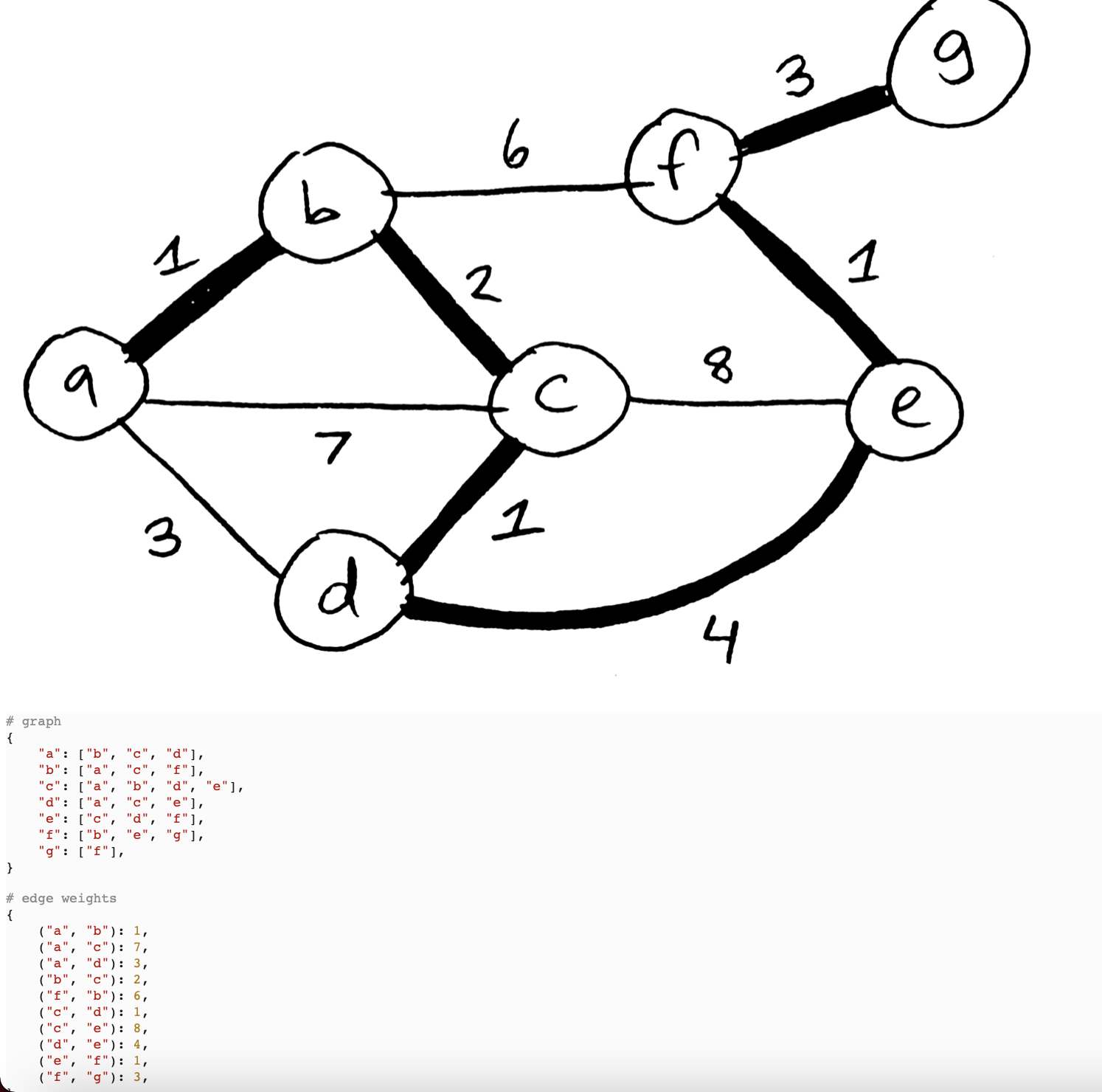
Here's an example graph, its adjacency list representation, and its edge weight dictionary. The edges in the graph's minimum spanning tree are bolded:

\fExample Here's an example of how your kruskals function should work: graph = { a" "d'lr "b" "d" : "e": "f": ["b" "g": [of" ], edges = . "b'j:1, "C'1: 7, ( "a", "d'): 3, ( "b', "c"): 2, ( "f", "b"): 6, ("c', "d'): 1, ( "c', "e") : 8, ( "d', "e"l: 4, ( "e", "f" ) : 1, ( "f' "g") : 3, met weight = kruskals (graph, edges) print (met_weight) # prints 12, total weight of MST found