package comp2402a2;

import java.util.AbstractList; import java.util.Collection;

/** * @author morin * * @param the type of objects stored in the List */ public class BlockedList extends AbstractList { /** * keeps track of the class of objects we store */ Factory f;

/** * The number of elements stored */ int n;

/** * The block size */ int b;

/** * Constructor * @param t the type of objects that are stored in this list * @param b the block size */ public BlockedList(Class t, int b) { f = new Factory(t); n = 0; // TODO: Implement this }

public int size() { return n; }

public T get(int i) { // TODO: Implement this if (i n - 1) throw new IndexOutOfBoundsException(); return null; }

public T set(int i, T x) { // TODO: Implement this if (i n - 1) throw new IndexOutOfBoundsException(); return null; }

public void add(int i, T x) { // TODO: Implement this if (i n) throw new IndexOutOfBoundsException(); }

public T remove(int i) { // TODO: Implement this if (i n - 1) throw new IndexOutOfBoundsException(); return null; } }

package comp2402a2;

import java.lang.reflect.Array;

public class Factory { Class t;

public Class type() { return t; } public Factory(Class t0) { t = t0; } @SuppressWarnings({"unchecked"}) protected T[] newArray(int n) { return (T[])Array.newInstance(t, n); }

public T newInstance() { T x; try { x = t.getDeclaredConstructor().newInstance(); } catch (Exception e) { x = null; } return x; } }

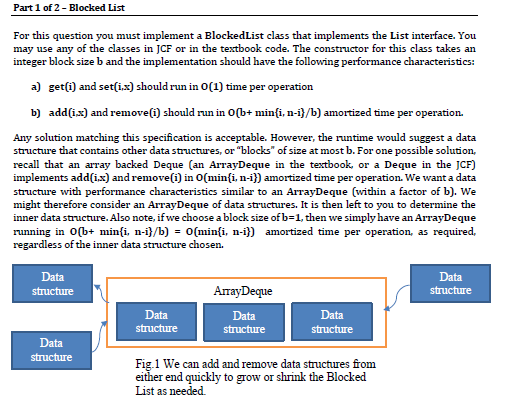
Part 1 of 2 -Blocked List For this question you must implement a BlockedList class that implements the List interface. You may use any of the classes in JCF or in the textbook code. The constructor for this class takes an integer block size b and the implementation should have the following performance characteristics a) get(i) and set(i.) should run in 0(1) time per operation b) add(ix) and remove(i) should run in O[b+ min{i, n-i}/b) amortized time per operation Any solution matching this specification is acceptable. However, the runtime would suggest a data structure that contains other data structures, or "blocks" of size at most b. For one possible solution, recall that an array backed Deque (an ArrayDeque in the textbook, or a Deque in the JCF) implements add(i.) and remove(i) in Omin{i, n-i}) amortized time per operation. We want a data structure with performance characteristics similar to an ArrayDeque (within a factor of b). We might therefore consider an ArrayDeque of data structures. It is then left to you to determine the inner data structure. Also note, if we choose a block size of b=1, then we simply have an ArrayDeque running in O(b+ min{i, n-i)/b) = 0(min{i, n-i)) amortized time per operation, as required, regardless of the inner data structure chosen. Data structure Data structure ArrayDeque Data structure Data structure Data structure Data structure Fig. 1 We can add and remove data structures from either end quickly to grow or shrink the Blocked List as needed Part 1 of 2 -Blocked List For this question you must implement a BlockedList class that implements the List interface. You may use any of the classes in JCF or in the textbook code. The constructor for this class takes an integer block size b and the implementation should have the following performance characteristics a) get(i) and set(i.) should run in 0(1) time per operation b) add(ix) and remove(i) should run in O[b+ min{i, n-i}/b) amortized time per operation Any solution matching this specification is acceptable. However, the runtime would suggest a data structure that contains other data structures, or "blocks" of size at most b. For one possible solution, recall that an array backed Deque (an ArrayDeque in the textbook, or a Deque in the JCF) implements add(i.) and remove(i) in Omin{i, n-i}) amortized time per operation. We want a data structure with performance characteristics similar to an ArrayDeque (within a factor of b). We might therefore consider an ArrayDeque of data structures. It is then left to you to determine the inner data structure. Also note, if we choose a block size of b=1, then we simply have an ArrayDeque running in O(b+ min{i, n-i)/b) = 0(min{i, n-i)) amortized time per operation, as required, regardless of the inner data structure chosen. Data structure Data structure ArrayDeque Data structure Data structure Data structure Data structure Fig. 1 We can add and remove data structures from either end quickly to grow or shrink the Blocked List as needed