package sortingsearching; public class GenericSortingMethods { //----------------------------------------------------------------- private static int numComps = 0; /** * swap procedure * @param Comparable[] a -- the array in which the swapping is done * @param i * @param j -- the two locations in the array that will be swapped */ public static void swap(Comparable[] a, int i, int j) { Comparable temp = a[i]; a[i] = a[j]; a[j] = temp; } //----------------------------------------------------------------- /** * findSmallestLoc -- Locates the smallest element in the array between * array positions start and end * @param int[] a -- the array in which the locating is to be done * @param start -- starting location * @param end -- end location * This is called by the selectionSort method */ public static int select(Comparable[] a, int k) { //find the location of the smallest element in the array //between position k and the end of the array int smallestPos = k; for (int j = k; j = 0) && (! done)) { // As long as the element in the array is > x, keep moving // it one position down. numComps++; if (a[k].compareTo(x)>0) { a[k+1] = a[k]; k--; } // Stop moving elements down as soon as you find an element >= x else { done = true; } } // Insert the new element at position k+1 a[k+1] = x; } //----------------------------------------------------------------- /** * pass: It makes one "pass" over the data, starting at position 0 up to * position end. It compares a[0] with a[1], a[1] with a[2] ... and * a[end-1] with a[end], and makes a swap if necessary. In case it swaps * it will record that fact by setting didSwap to true. This is what is * returned by the method. * @param Comparable[] a -- the array to be sorted * @param end -- 0 to end is the part of the array to focus on. The elements * at positions end+1 ... will be sorted. */ public static boolean pass(Comparable[] a, int end) { boolean didSwap = false; for (int k = 0; k 0) { swap(a, k, k+1); didSwap = true; } } return didSwap; } //----------------------------------------------------------------- /** * The bubblesort method. It makes as many "pass"es as needed over the * array until it is sorted. * @param Comparable[] a -- the array to be sorted * Time Complexity: O(N ** 2) */ public static void bubbleSort(Comparable[] a) { numComps = 0; boolean swapped = true; // Keep track of whether we made a swap in this pass // Initially set to true, because we have to make at // least one pass int passCount = 0; // Counts the number of passes. We need no more than // n-1 passes, where n is the length of the array int end = a.length-1; // 0 to end is the part of the array to focus on // Loop as long as passCount = 0)) { numComps++; //System.out.println("Numcomps = "+numComps); up++; } while ( pivot.compareTo(a[down]) 0) l = mid+1; else h = mid-1; } return -1; } /** * It is auumed that: * Two parts of the array a: a[start1] to a[start2-1] and * a[start2] to a[end2] are sorted. end2 >= start2 >= start1 * This will merge those two parts to make one long * sorted part between a[start1] to a[end2] */ public static void merge(Comparable[] a, int start1, int start2, int end2) { int c1 = start1; //Counter for the first half of the sorted array int c2 = start2; //Counter for the second half of the sorted array int sortedCounter = 0; //Counter for the sorted array //Temporary array for the merged elements Object [] b = new Object[end2 - start1 +1]; //Scan the sorted array a and keep filling b by elements from a or //b, depending on which is smaller while (c1 a[c2], move a[c2] into b and increment c2 else if (a[c1].compareTo(a[c2]) > 0) { b[sortedCounter] = a[c2]; sortedCounter++; c2++; numComps++; } //If a[c1] == a[c2], move both a[c1] and a[c2] into b and //increment both c1 and c2 else { b[sortedCounter] = a[c1]; sortedCounter++; b[sortedCounter] = a[c2]; sortedCounter++; c1++; c2++; } } //Copy the rest of the elements from first half while (c1 1) { mergeSort(a, start, start+half-1); //sort first half mergeSort(a, start+half, end);//sort second half merge(a, start, start+half, end); } } public static void heapInsert(Comparable [] a, int size, Comparable x) { // Assume: a[0] ... a[size-1] is a heap // Insert x and still keep heap property //a[size] = x; add x at the end of a //---------------------------------------------------------- // compare x to its parent; if x = 0) { if (a[k].compareTo(a[(k-1)/2]) = b[2*k+1]) && (b[k] >= b[2*k+2])) // >= both children if ((b[k].compareTo(b[2*k+1]) >= 0) && (b[k].compareTo(b[2*k+2]) >= 0)) return; //if ((b[k] >= b[2*k+1]) || (b[k] >= b[2*k+2])) // >= one child if ((b[k].compareTo(b[2*k+1]) >= 0) || (b[k].compareTo(b[2*k+2]) >= 0)) //if (b[2*k+2] >= b[2*k+1]) if (b[2*k+2].compareTo(b[2*k+1]) >= 0) loc = 2*k+2; else loc = 2*k+1; else // = b[2*k+2]) if (b[2*k+1].compareTo(b[2*k+2]) >= 0) loc = 2*k+1; else loc = 2*k+2; } else if (2*k+1 = b[2*k+1]) if(b[k].compareTo(b[2*k]) >= 0) return; loc = 2*k+1; } numComps++; // Do the swap and go back to loop swap(b, k, loc); k = loc; //System.out.println("k = " + k); } } public static void heapSort(Comparable[] a) { numComps = 0; for (int k = 1; k 0) { // move the first element into the last location and leave it there swap(a, 0, size-1); // Now focus on the shorter array size = size - 1; adjust(a, size); } System.out.println("NumComps = "+numComps); } }

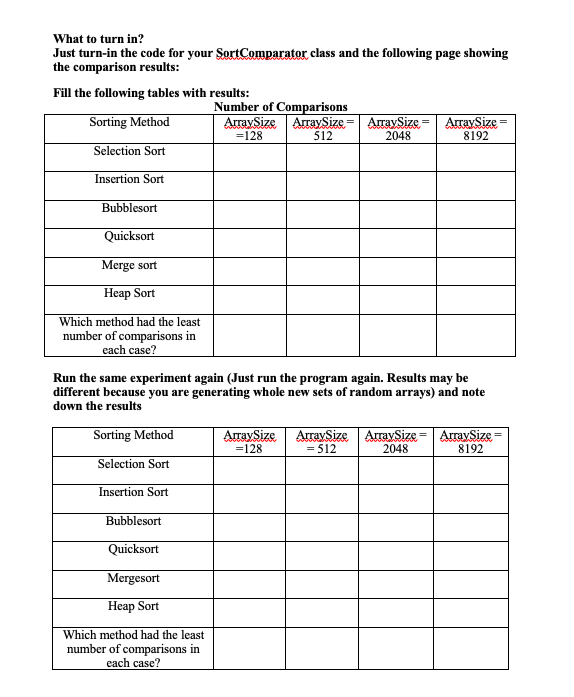
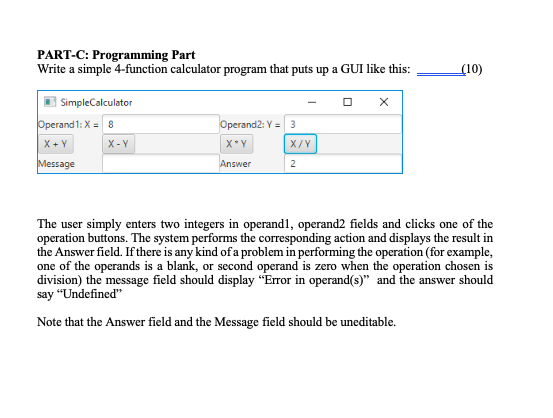
PART-B: Comparison of Sorting Methods Do the following experiments data into the tables at the end. You are given Java code for a class called (10) to compare the efficiencies of sorting methods and fill in the that contains code for five sorting methods. (Download it from Blackboard, under Java code/Generic Sorter). The method signatures are as follows public static void selectionsot (Comparable[ a) public static void insertionsot (Comparable a]) public static void bubbleSoxt(Comparable[l a) public static void guiskSort(Comparable[] a) public static void mergeSot(Comparable[] a) public static void heapSort (Comparable[] a) You are asked to run experiments with arrays of various sizes (specified in the table below) containing random data (you have to generate the data) and fill in the table with the number of comparisons reported by each sorting method for each specified size of the array. This experiment is conducted twice . Create a package called sortingscarching .Create a class called GenericSortingMethods. Copy and paste the code for this class from Blackboard (Under Java Code) Write a class called SortComparator which contains the public static void main method. It should do the following: . 1. Create an Integer array of size 128. Call it a. 2. Fill it up with random numbers between 0 and 100,000. Use for (int k -0; k