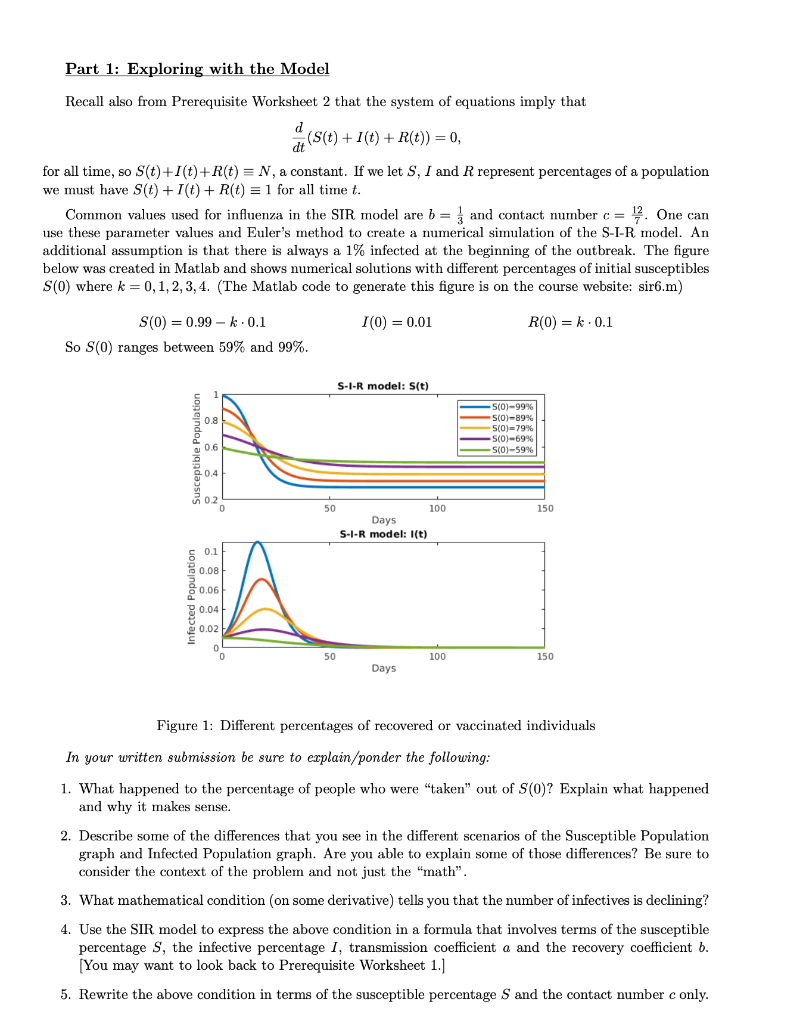
Part 1: Exploring with the Model Recall also from Prerequisite Worksheet 2 that the system of equations imply that de(s(t) + 2() + R(t)) = 0, for all time, so S(t)+I(t)+R(t) = N, a constant. If we let S, I and R represent percentages of a population we must have s(t) +1(t) +R(t) = 1 for all time t. Common values used for influenza in the SIR model are b = and contact number c= 12. One can use these parameter values and Euler's method to create a numerical simulation of the S-I-R model. An additional assumption is that there is always a 1% infected at the beginning of the outbreak. The figure below was created in Matlab and shows numerical solutions with different percentages of initial susceptibles S(0) where k = 0,1,2, 3, 4. (The Matlab code to generate this figure is on the course website: sir6.m) I(0) = 0.01 R(0) = k0.1 S(0) = 0.99 - k. 0.1 So S(0) ranges between 59% and 99%. S-I-R model: S(t) 5(0)-99% 5(0)-89% S(0)=79% 5(0)-69% S(O)-59% 0.6 00.4 150 50 100 Days S-I-R model: I(t) 0.1 0.08 0.06 0.04 20.02 0 50 100 150 Days Figure 1: Different percentages of recovered or vaccinated individuals In your written submission be sure to explain/ponder the following: 1. What happened to the percentage of people who were taken" out of S(0)? Explain what happened and why it makes sense. 2. Describe some of the differences that you see in the different scenarios of the Susceptible Population graph and Infected Population graph. Are you able to explain some of those differences? Be sure to consider the context of the problem and not just the "math". 3. What mathematical condition (on some derivative) tells you that the number of infectives is declining? 4. Use the SIR model to express the above condition in a formula that involves terms of the susceptible percentage S, the infective percentage 1, transmission coefficient a and the recovery coefficient b. [You may want to look back to Prerequisite Worksheet 1.) 5. Rewrite the above condition in terms of the susceptible percentage S and the contact number c only. Part 1: Exploring with the Model Recall also from Prerequisite Worksheet 2 that the system of equations imply that de(s(t) + 2() + R(t)) = 0, for all time, so S(t)+I(t)+R(t) = N, a constant. If we let S, I and R represent percentages of a population we must have s(t) +1(t) +R(t) = 1 for all time t. Common values used for influenza in the SIR model are b = and contact number c= 12. One can use these parameter values and Euler's method to create a numerical simulation of the S-I-R model. An additional assumption is that there is always a 1% infected at the beginning of the outbreak. The figure below was created in Matlab and shows numerical solutions with different percentages of initial susceptibles S(0) where k = 0,1,2, 3, 4. (The Matlab code to generate this figure is on the course website: sir6.m) I(0) = 0.01 R(0) = k0.1 S(0) = 0.99 - k. 0.1 So S(0) ranges between 59% and 99%. S-I-R model: S(t) 5(0)-99% 5(0)-89% S(0)=79% 5(0)-69% S(O)-59% 0.6 00.4 150 50 100 Days S-I-R model: I(t) 0.1 0.08 0.06 0.04 20.02 0 50 100 150 Days Figure 1: Different percentages of recovered or vaccinated individuals In your written submission be sure to explain/ponder the following: 1. What happened to the percentage of people who were taken" out of S(0)? Explain what happened and why it makes sense. 2. Describe some of the differences that you see in the different scenarios of the Susceptible Population graph and Infected Population graph. Are you able to explain some of those differences? Be sure to consider the context of the problem and not just the "math". 3. What mathematical condition (on some derivative) tells you that the number of infectives is declining? 4. Use the SIR model to express the above condition in a formula that involves terms of the susceptible percentage S, the infective percentage 1, transmission coefficient a and the recovery coefficient b. [You may want to look back to Prerequisite Worksheet 1.) 5. Rewrite the above condition in terms of the susceptible percentage S and the contact number c only