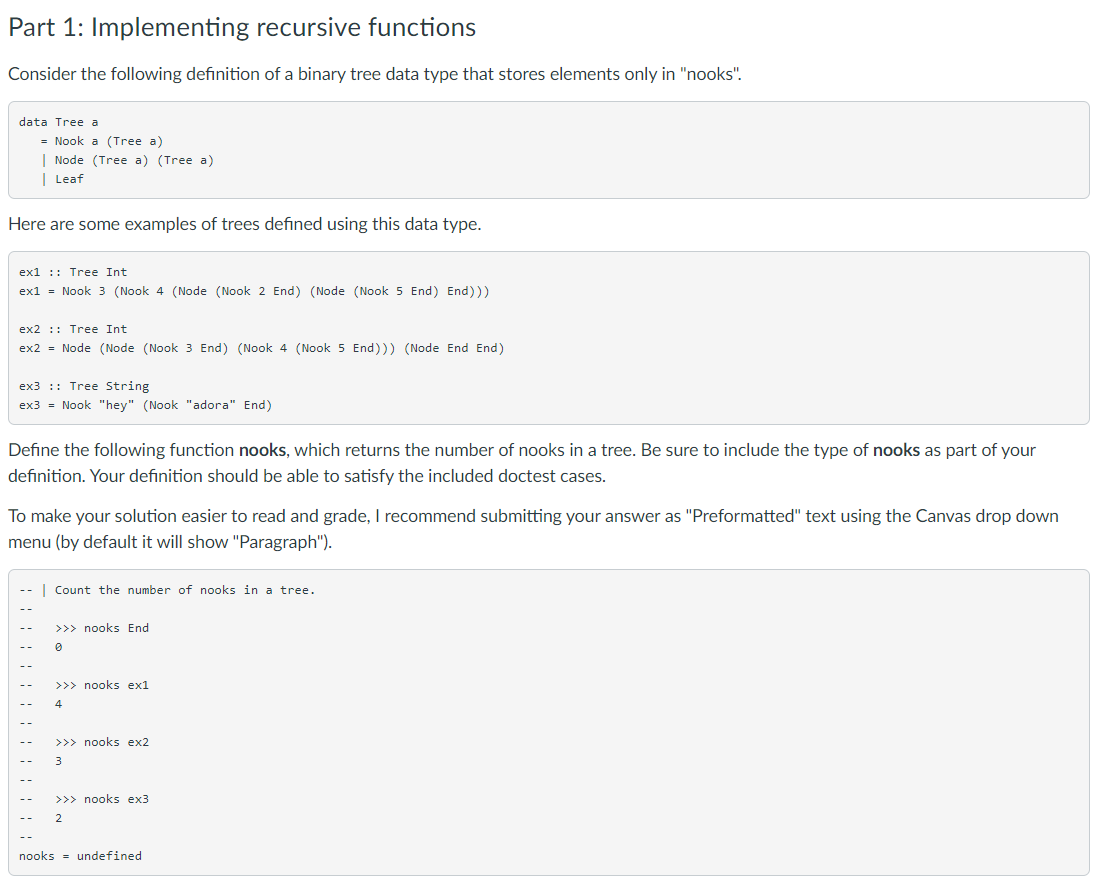

Part 1: Implementing recursive functions Consider the following definition of a binary tree data type that stores elements only in "nooks". data Tree a = Nook a (Tree a) Node (Tree a) (Tree a) | Leaf Here are some examples of trees defined using this data type. exl :: Tree Int ex1 = Nook 3 (Nook 4 (Node (Nook 2 End) (Node (Nook 5 End) End))) ex2 :: Tree Int ex2 = Node (Node (Nook 3 End) (Nook 4 (Nook 5 End))) (Node End End) ex3 :: Tree String ex3 = Nook "hey" (Nook "adora" End) Define the following function nooks, which returns the number of nooks in a tree. Be sure to include the type of nooks as part of your definition. Your definition should be able to satisfy the included doctest cases. To make your solution easier to read and grade, I recommend submitting your answer as "Preformatted" text using the Canvas drop down menu (by default it will show "Paragraph"). -- Count the number of nooks in a tree. >>> nooks End >>> nooks ex1 4 >>> nooks ex2 3 n n >>> nooks ex3 2 nooks = undefined Part 1 (continued): Implementing recursive functions Define the following function mapTree, which maps a function over values of the Tree data type defined above. Be sure to include the type of mapTree as part of your definition. Your definition should be able to satisfy the included doctest cases. As before, I recommend submitting your answer as "Preformatted" text using the Canvas drop down menu. -- | Map a function over a tree, preserving its structure. >>> mapTree (+10) ex1 Nook 13 (Nook 14 (Node (Nook 12 End) (Node (Nook 15 End) End))) >>> mapTree odd ex2 Node (Node (Nook True End) (Nook False (Nook True End))) (Node End End) >>> mapTree length ex3 Nook 3 (Nook 5 End) mapTree = undefined Part 1: Implementing recursive functions Consider the following definition of a binary tree data type that stores elements only in "nooks". data Tree a = Nook a (Tree a) Node (Tree a) (Tree a) | Leaf Here are some examples of trees defined using this data type. exl :: Tree Int ex1 = Nook 3 (Nook 4 (Node (Nook 2 End) (Node (Nook 5 End) End))) ex2 :: Tree Int ex2 = Node (Node (Nook 3 End) (Nook 4 (Nook 5 End))) (Node End End) ex3 :: Tree String ex3 = Nook "hey" (Nook "adora" End) Define the following function nooks, which returns the number of nooks in a tree. Be sure to include the type of nooks as part of your definition. Your definition should be able to satisfy the included doctest cases. To make your solution easier to read and grade, I recommend submitting your answer as "Preformatted" text using the Canvas drop down menu (by default it will show "Paragraph"). -- Count the number of nooks in a tree. >>> nooks End >>> nooks ex1 4 >>> nooks ex2 3 n n >>> nooks ex3 2 nooks = undefined Part 1 (continued): Implementing recursive functions Define the following function mapTree, which maps a function over values of the Tree data type defined above. Be sure to include the type of mapTree as part of your definition. Your definition should be able to satisfy the included doctest cases. As before, I recommend submitting your answer as "Preformatted" text using the Canvas drop down menu. -- | Map a function over a tree, preserving its structure. >>> mapTree (+10) ex1 Nook 13 (Nook 14 (Node (Nook 12 End) (Node (Nook 15 End) End))) >>> mapTree odd ex2 Node (Node (Nook True End) (Nook False (Nook True End))) (Node End End) >>> mapTree length ex3 Nook 3 (Nook 5 End) mapTree = undefined








