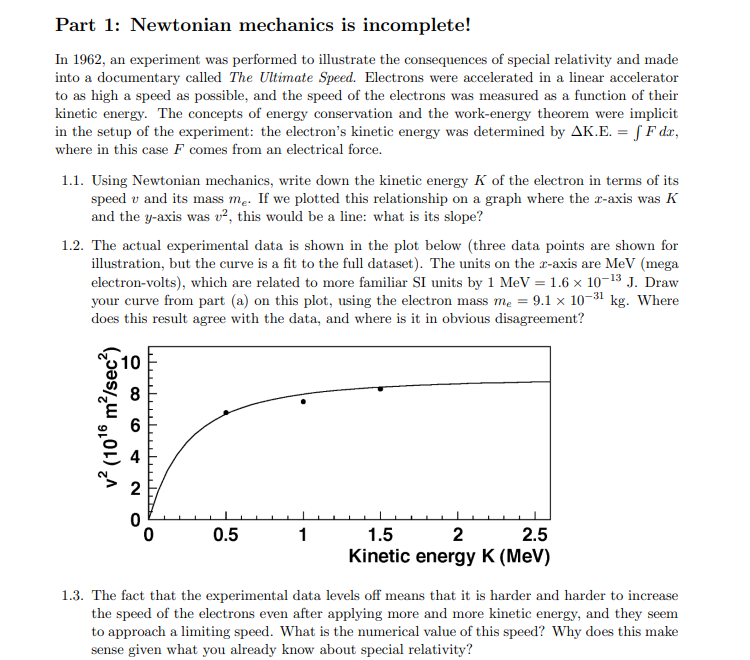
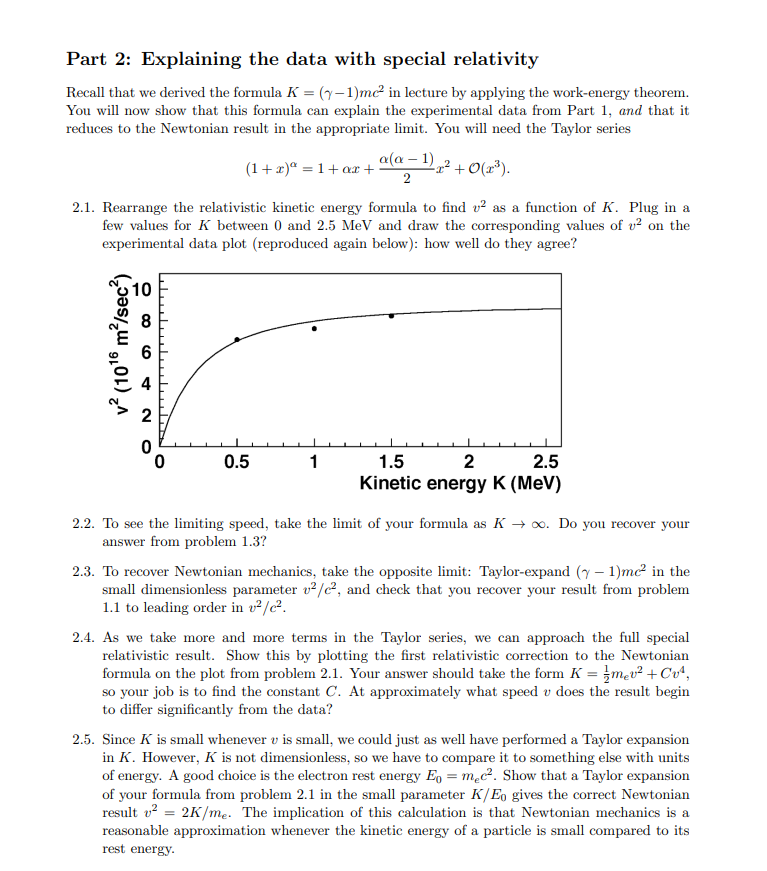
Part 1: Newtonian mechanics is incomplete! In 1962, an experiment was performed to illustrate the consequences of special relativity and made into a documentary called The Ultimate Speed. Electrons were accelerated in a linear accelerator to as high a speed as possible, and the speed of the electrons was measured as a function of their kinetic energy. The concepts of energy conservation and the work-energy theorem were implicit in the setup of the experiment: the electron's kinetic energy was determined by AK.E. = [Fdx, where in this case F comes from an electrical force. 1.1. Using Newtonian mechanics, write down the kinetic energy K of the electron in terms of its speed v and its mass me. If we plotted this relationship on a graph where the x-axis was K and the y-axis was v, this would be a line: what is its slope? 1.2. The actual experimental data is shown in the plot below (three data points are shown for illustration, but the curve is a fit to the full dataset). The units on the x-axis are MeV (mega electron-volts), which are related to more familiar SI units by 1 MeV = 1.6 10-13 J. Draw your curve from part (a) on this plot, using the electron mass me = 9.1 x 10-31 kg. Where does this result agree with the data, and where is it in obvious disagreement? v (1016 m/sec) 086 4 2 0.5 1 1.5 2 2.5 Kinetic energy K (MeV) 1.3. The fact that the experimental data levels off means that it is harder and harder to increase the speed of the electrons even after applying more and more kinetic energy, and they seem to approach a limiting speed. What is the numerical value of this speed? Why does this make sense given what you already know about special relativity? Part 2: Explaining the data with special relativity Recall that we derived the formula K = (y-1)mc in lecture by applying the work-energy theorem. You will now show that this formula can explain the experimental data from Part 1, and that it reduces to the Newtonian result in the appropriate limit. You will need the Taylor series (1+x)=1+ax + a(a-1) 1) x+0(x). 2 2.1. Rearrange the relativistic kinetic energy formula to find v as a function of K. Plug in a few values for K between 0 and 2.5 MeV and draw the corresponding values of v on the experimental data plot (reproduced again below): how well do they agree? v (1016 m/sec) 10 0 60 4 2 0 0 0.5 1 1.5 2 2.5 Kinetic energy K (MeV) 2.2. To see the limiting speed, take the limit of your formula as K. Do you recover your answer from problem 1.3? 2.3. To recover Newtonian mechanics, take the opposite limit: Taylor-expand (y-1)mc in the small dimensionless parameter v/c, and check that you recover your result from problem 1.1 to leading order in v/c. 2.4. As we take more and more terms in the Taylor series, we can approach the full special relativistic result. Show this by plotting the first relativistic correction to the Newtonian formula on the plot from problem 2.1. Your answer should take the form K = mev + Cv, so your job is to find the constant C. At approximately what speed v does the result begin to differ significantly from the data? 2.5. Since K is small whenever v is small, we could just as well have performed a Taylor expansion in K. However, K is not dimensionless, so we have to compare it to something else with units of energy. A good choice is the electron rest energy E = mc2. Show that a Taylor expansion of your formula from problem 2.1 in the small parameter K/Eo gives the correct Newtonian result 22K/me. The implication of this calculation is that Newtonian mechanics is a reasonable approximation whenever the kinetic energy of a particle is small compared to its rest energy. Part 3: A first look at relativistic kinematics with photons We have already seen in several ways that it takes an infinite amount of energy to accelerate a massive particle to the speed of light. A massless particle would make no sense in Newtonian mechanics (since all of the kinematic formulas like F=ma and K = m would just give zero), but such particles are important features of special relativity. The most common example is the photon, which is a particle of light. 3.1. Take the ratio of the relativistic momentum and energy formulas to derive a useful formula for the velocity of a particle: p/E = v/c. Notice that this formula does not involve the mass! 3.2. Suppose we boldly assert that p/E = v/c still applies when v = c. In that case, we could still assign an energy and a momentum to a photon, related by Pphoton = Ephoton/c. Rearrange this formula to show Ehoton - Pphoton c2 = 0. 3.3. Use the relativistic momentum and energy formulas for a massive particle to show that E pc = mc. This is probably the single most important formula for the remainder of the course! And by your work in problem 3.2, it also applies for a massless particle with m = 0. 3.4. Since a particle at rest has E = Eo, it can convert its rest energy into other forms of energy. In particular, there is an unstable subatomic particle called the 0 (pronounced "pi-zero" or "neutral pion") which decays into two photons. Use the results of problems 3.2 and 3.3 to determine the energies of the two photons in terms of the mass of the pion m. To do this, you can work in the rest frame of the pion, and assume that the photons' momentum vectors are aligned with their velocity vectors (this will be fully justified in a few weeks). First apply momentum conservation, followed by energy conservation.