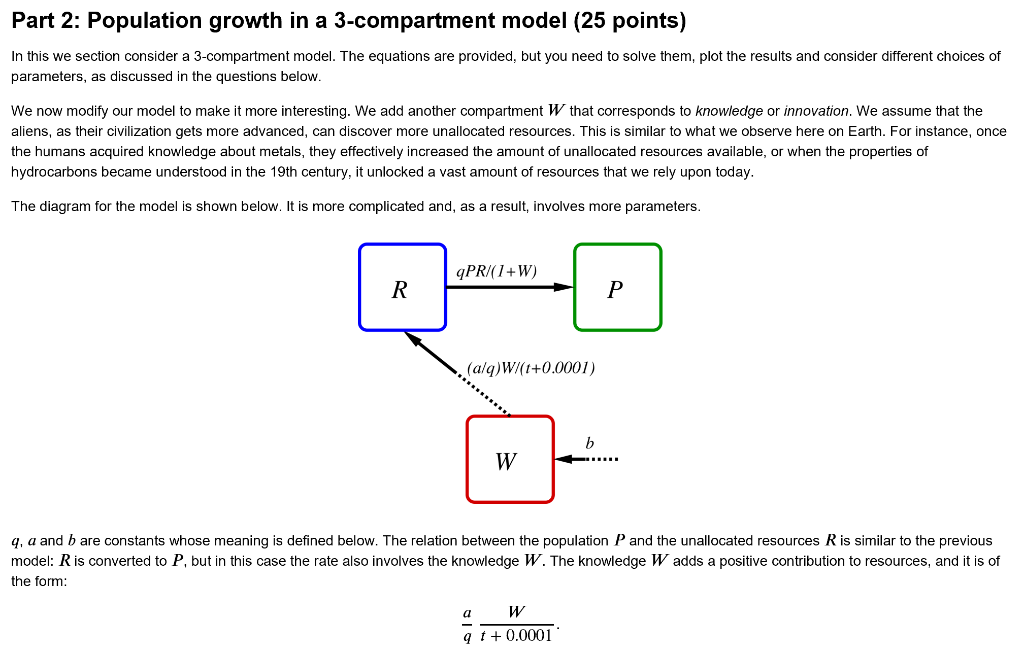
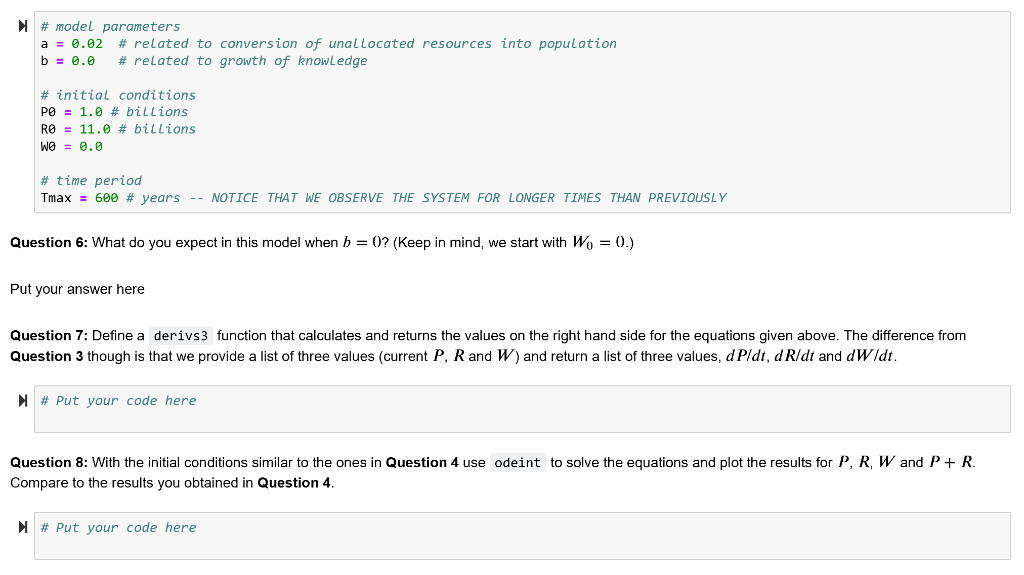
Part 2: Population growth in a 3-compartment model (25 points) In this we section consider a 3-compartment model. The equations are provided, but you need to solve them, plot the results and consider different choices of parameters, as discussed in the questions below We now modify our model to make it more interesting. We add another compartment W that corresponds to knowledge or innovation. We assume that the aliens, as their civilization gets more advanced, can discover more unallocated resources. This is similar to what we observe here on Earth. For instance, once the humans acquired knowledge about metals, they effectively increased the amount of unallocated resources available, or when the properties of hydrocarbons became understood in the 19th century, it unlocked a vast amount of resources that we rely upon today. The diagram for the model is shown below. It is more complicated and, as a result, involves more parameters qPRI(1+W) .(aq)W/(i0.0001) q, a and b are constants whose meaning is defined below. The relation between the population P and the unallocated resources R is similar to the previous model: R is converted to P, but in this case the rate also involves the knowledge W. The knowledge W adds a positive contribution to resources, and it is of the form: a W 1+0.000T (The little positive constant 0.0001 in the denominator is added to avoid division by 0 at t = 0, but effectively this term behaves as w.) The dashed end of the arrow on the W compartment represents the fact that while knowledge contributes to the resources, it does not decrease because of that. We can interpret such term in the following way: more knowledge "unlocks" more resources. For instance, if we have technology that a car can run 10 miles per gallon of gas, and then we learn a new technology that it can run 30 miles per gallon this is as if we tripled the amount of the available resource. The ~ 1/t part means that although knowledge grows, it gets harder with time to keep adding to the resources The arrow entering the W compartment means that in this model the knowledge keeps increasing at some constant rate b The first-order differential equations that correspond to the diagram above are: dP PR dR dt dW dt PR a W +q 0.0001 = b. As before, the initial values of the population and resources at time I = 0 be P(1-0) W(t = 0) = W) = 0. This time we define Po and R(1-0) = R0. For the knowledge we will always choose a+b where a is a parameter similar to the simpler 2-compartment model in Part 1, b controls the rate of acquiring knowledge and c PRo Again a, b, c and, as a result, q are constants, while P, R and W are functions of time t. To get started we can use the values given below. # model parameters a : 0.02 # related to conversion of una L Located resources into population b = 0.0 # related to growth of knowledge # initial conditions P0-1.0 # billions RO : 11.0 # billions # time period Tmax 600 # years --NOTICE THAT WE OBSERVE THE SYSTEM FOR LONGER TIMES THAN PREVIOUSLY Question 6: What do you expect in this model when b = 07(Keep in mind, we start with wo = 0) Put your answer here Question 7: Define a derivs3 function that calculates and returns the values on the right hand side for the equations given above. The difference from Question 3 though is that we provide a list of three values (current P, R and W) and return a list of three values, d Pldt, d R/dt and dWldi. # Put your code here Question 8: With the initial conditions similar to the ones in Question 4 use odeint to solve the equations and plot the results for P, R, W and P+ R. Compare to the results you obtained in Question 4 # Put your code here Let us now change the parameters to the following # model parameters a = 0.02 # related to conversion of unallocated resources into population b-0.001 # related to growth of knowledge # initial conditions P0-1.0 # billions R0-11.0 # billions WO0.0 # time period Tmax 600 # years Question 9: Solve the equations, as you did in Question 8 and plot the results. Do you observe any differences? Write your comments in the mark down cell below # Put your code here Put your answer here Question 10: The aliens want to inhabit an empty planet with no resources. They have a finite amount of space in their ships, so they have two choices 1. Take five billion aliens and one billion resources (P-5, Ro1) 2. Take one billion aliens and five billion resources (Po, Ro-5) If their goal is to maximize the population after 200 years, which option should they take? If they want to maximize the population after 600 years, which option should they take? Solve the equations for both scenarios and plot the population P for both cases as function of time on the same plot. Use the rest of the parameters as given below Make sure you a u recors youreresponses to the questions in the mark down cell below! r responses to the questions in the mark down cell below! 5b41ce97e2a42648b70c2e38961 98dcdd68847 b407 # model parameters a : 0.02 # related to conversion of unaLLocated resources into population b : 0.0001 # related to growth of knowledge WO : 0.0 # initial amount of knowledge # time period Tmax = 600 # years # Put your code here Put your answer here Question 11: The aliens want to inhabit another planet with no resources. They can afford to send one billion aliens with one billion resources (Po1 and Ro ). This time they can equip their space explorers differently, they have two options I. Provide the tools and equipment that correspond to the rates: a = 0.03 and b = 0.0005. Recall that a controls how fast we convert the unallocated resources into population and b controls the rate of growth of knowledge. 2. Take less equipment, so a would drop by an order of magnitude, but take more tools that would increase b by an order of magnitude, i.e. a 0.003 and b = 0.005. If their goal is to maximize the population after 200 years, which option should they take? If they want to maximize the population after 600 years, which option should they take Solve the equations for both scenarios and plot the population P for both cases as function of time on the same plot. Use the rest of the parameters as given below. Make sure you record your responses to the questions in the mark down cell below! H # initial conditions P0-1.0 # billions R0-1.0 # billions # time period Tmax 600 # years # Put your code here Put your answer here Part 2: Population growth in a 3-compartment model (25 points) In this we section consider a 3-compartment model. The equations are provided, but you need to solve them, plot the results and consider different choices of parameters, as discussed in the questions below We now modify our model to make it more interesting. We add another compartment W that corresponds to knowledge or innovation. We assume that the aliens, as their civilization gets more advanced, can discover more unallocated resources. This is similar to what we observe here on Earth. For instance, once the humans acquired knowledge about metals, they effectively increased the amount of unallocated resources available, or when the properties of hydrocarbons became understood in the 19th century, it unlocked a vast amount of resources that we rely upon today. The diagram for the model is shown below. It is more complicated and, as a result, involves more parameters qPRI(1+W) .(aq)W/(i0.0001) q, a and b are constants whose meaning is defined below. The relation between the population P and the unallocated resources R is similar to the previous model: R is converted to P, but in this case the rate also involves the knowledge W. The knowledge W adds a positive contribution to resources, and it is of the form: a W 1+0.000T (The little positive constant 0.0001 in the denominator is added to avoid division by 0 at t = 0, but effectively this term behaves as w.) The dashed end of the arrow on the W compartment represents the fact that while knowledge contributes to the resources, it does not decrease because of that. We can interpret such term in the following way: more knowledge "unlocks" more resources. For instance, if we have technology that a car can run 10 miles per gallon of gas, and then we learn a new technology that it can run 30 miles per gallon this is as if we tripled the amount of the available resource. The ~ 1/t part means that although knowledge grows, it gets harder with time to keep adding to the resources The arrow entering the W compartment means that in this model the knowledge keeps increasing at some constant rate b The first-order differential equations that correspond to the diagram above are: dP PR dR dt dW dt PR a W +q 0.0001 = b. As before, the initial values of the population and resources at time I = 0 be P(1-0) W(t = 0) = W) = 0. This time we define Po and R(1-0) = R0. For the knowledge we will always choose a+b where a is a parameter similar to the simpler 2-compartment model in Part 1, b controls the rate of acquiring knowledge and c PRo Again a, b, c and, as a result, q are constants, while P, R and W are functions of time t. To get started we can use the values given below. # model parameters a : 0.02 # related to conversion of una L Located resources into population b = 0.0 # related to growth of knowledge # initial conditions P0-1.0 # billions RO : 11.0 # billions # time period Tmax 600 # years --NOTICE THAT WE OBSERVE THE SYSTEM FOR LONGER TIMES THAN PREVIOUSLY Question 6: What do you expect in this model when b = 07(Keep in mind, we start with wo = 0) Put your answer here Question 7: Define a derivs3 function that calculates and returns the values on the right hand side for the equations given above. The difference from Question 3 though is that we provide a list of three values (current P, R and W) and return a list of three values, d Pldt, d R/dt and dWldi. # Put your code here Question 8: With the initial conditions similar to the ones in Question 4 use odeint to solve the equations and plot the results for P, R, W and P+ R. Compare to the results you obtained in Question 4 # Put your code here Let us now change the parameters to the following # model parameters a = 0.02 # related to conversion of unallocated resources into population b-0.001 # related to growth of knowledge # initial conditions P0-1.0 # billions R0-11.0 # billions WO0.0 # time period Tmax 600 # years Question 9: Solve the equations, as you did in Question 8 and plot the results. Do you observe any differences? Write your comments in the mark down cell below # Put your code here Put your answer here Question 10: The aliens want to inhabit an empty planet with no resources. They have a finite amount of space in their ships, so they have two choices 1. Take five billion aliens and one billion resources (P-5, Ro1) 2. Take one billion aliens and five billion resources (Po, Ro-5) If their goal is to maximize the population after 200 years, which option should they take? If they want to maximize the population after 600 years, which option should they take? Solve the equations for both scenarios and plot the population P for both cases as function of time on the same plot. Use the rest of the parameters as given below Make sure you a u recors youreresponses to the questions in the mark down cell below! r responses to the questions in the mark down cell below! 5b41ce97e2a42648b70c2e38961 98dcdd68847 b407 # model parameters a : 0.02 # related to conversion of unaLLocated resources into population b : 0.0001 # related to growth of knowledge WO : 0.0 # initial amount of knowledge # time period Tmax = 600 # years # Put your code here Put your answer here Question 11: The aliens want to inhabit another planet with no resources. They can afford to send one billion aliens with one billion resources (Po1 and Ro ). This time they can equip their space explorers differently, they have two options I. Provide the tools and equipment that correspond to the rates: a = 0.03 and b = 0.0005. Recall that a controls how fast we convert the unallocated resources into population and b controls the rate of growth of knowledge. 2. Take less equipment, so a would drop by an order of magnitude, but take more tools that would increase b by an order of magnitude, i.e. a 0.003 and b = 0.005. If their goal is to maximize the population after 200 years, which option should they take? If they want to maximize the population after 600 years, which option should they take Solve the equations for both scenarios and plot the population P for both cases as function of time on the same plot. Use the rest of the parameters as given below. Make sure you record your responses to the questions in the mark down cell below! H # initial conditions P0-1.0 # billions R0-1.0 # billions # time period Tmax 600 # years # Put your code here Put your answer here