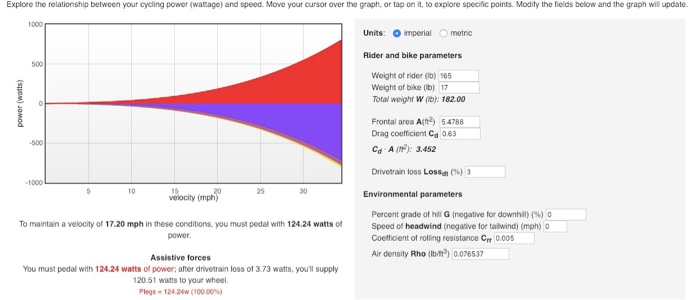
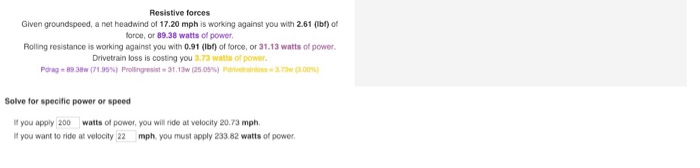
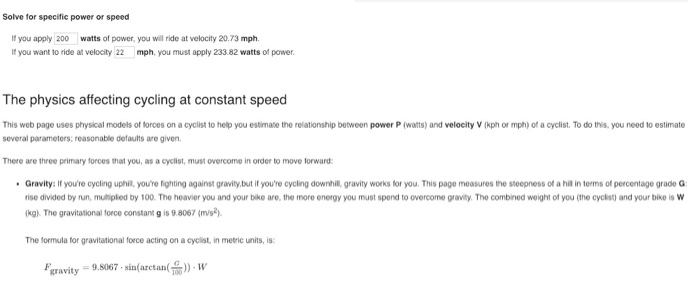
Part 2: Power you complete part 1, continue on to part 2 In part 2 you'll compute some more complex information about cyclying, including the power in watts that the cyclist needs to apply to the pedal to move at the velocity we calculated above. Sample session for part 2 (highlighted text means that the user has typed this information at the console): How steep is the hill you're climbing (%)? 3 How much do you weigh (in kg) 95 How much does your bike weigh (in kg) 7 What is your frontal area (in m*2)2 0.509 What is the windspeed (in km/h)? 20 What is the air density (in kg/m 3) 1.22 Grade of hill: 3.0% Rider weight: 95.0kg Bike weight: 7.0kg Frontal area of rider 0.509m 2 Windspeed: 20.0km/h Air density: 1.22kg/m 3 The rolling resistance for your bike is assumed to be 0.005 Your drag coefficient is assumed to be 0.63. your drive train loss is assumed to be 38. Force of gravity: 29.9950N Force of rolling resistance: 4.9992N Force of drag: 43.3094N Total force of reistance: 78.3036N Power applied to wheels: 730.1222w Power from your legs: 752.7033w Programmed by the Instructors Date: Thu Jan 17 11:59:46 2019 End of processing Explore the relationship between your cycling power (wattage) and speed. Move your cursor over the graph, or tap on it, to explore specific points. Modify the fields below and the graph will update 1000 Units: imperial metric Rider and bike parameters 500 Weight of rider (Ib) 165 Weight of bike (ib) T7 Total weight W (ib): 18200 Frontal area 54788 Drag coefficient Cd 0.63 Cd A (: 3.452 500 Drivetrain loss Lossdt(76) 3 1000 10 25 30 20 velocity (mph) Percent grade of hil G (negative for downhil) (%) 0 Speed of headwind (negative for talwind) (mph) Coetficient of rolling resistance Cr 0.00 Air density Rho (Ibtt) o076537 To maintain a velocity of 17.20 mph in these conditions, you must pedal with 124.24 watts of power Assistive forces You must pedal with 124.24 watts of power, after drivetrain loss of 3.73 watts, youll supply 20.51 watts to your wheel. Plegs " 12424w (10000%) Resistive forces Given groundspeed, a net headwind of 17.20 mph is working against you with 2.61 (bf) of force, or 89.38 watts of power Rolling resistance is working against you with 0.91 (lbf) of foroe, or 31.13 watts of power Drivetrain loss is costng you 37a watts of power Parag-8938m(7195%) Pollngesista 31.13w(25OS%) Panetarto",373m(300%) Solve for specific power or speed Iyou apply 200 watts of power, you will ride at velocity 20.73 mph. If you want to ride at velocity 22 mph, you must apply 23382 watts of power Solve for specific power or speed If you apply 200 watts of power, you will ride at velocity 20.73 mph. It you want to ride at velocity 22 mph, you must apply 233.82 watts of power The physics affecting cycling at constant speed This web page uses physical models of forces on a cyclist to help you estimate the relationship between power P (wats) and velocity V (kph or mph) of a cyclist. To do this, you need to estimate several parameters; reasonable defaults are given. There are three primary forces that you, as a cyclist, must overcome in order to move forward Gravity: If you're cycling uphil, youre fighting against gravity,but if you're cycling downhill, gravity works for you. This page measures the steepness of a hill in terms of percentage gradeG rise divided by run, mutipled by 100. The heavier you and your bike are, the more energy you must spend to overcome gravity. The combined weight of you (the cyclist) and your bike is W kg). The gravitational force constant g is 9.8067 (m/s) The formula for gravitational force acting on a cyclist, in metric units, is gravity = 9.S67 , sin(arctan( )-W Rolling resistance: Friction between your tires and the road surface slows you down. The bumpier the road, the more friction youll experience; the higher quality your tires and tube, the less friction youll experience. As well, the heavier you and your bike are, the more friction youll experience. There is a dimensionless parameter, called the coefficient of roling resistance, or C that captures the bumpiness of the road and the quality of your tres. The formula for the roilling resistance acting on a cyclist, in metric units, is Frolling-M8067 . cos(arctan( )) . w . c., Aerodynamic drag: As you cycle through the air, your bike and body need to push the air around you, similar to how a snowplow pushes snow out of the way Because of this, the air exerts a force against you as you ride. There are a few things that dictate how much force the air exerts against you. The faster you ride, velocity V (m/s), the more foroe the air pushes against you. As well, you and your bike present a cortain frontal aroa A (m2 to the air. The larger this frontal aroa, the more air you have to displace, and the larger the force the air pushes against you. This i why cyclists and bike manufacturers try hard to minimize frontal area in an aerodynamc position. The air density Rho (kg/m2) is also important: the more dense the air, the more force it exerts on you Finally, there are other effects, like the slipperyness of your clothing and the degree to which air flows laminarly rather than turbulentily around you and your bike. Optimizing your aerodynamic positions also help with this. These other effects are captured in another dimensionless parameter called the drag coolficient,or Co. Sometimes you will see people talking about Cd A,or CdA. This is just the drag coefficient Cd multiplied by the frontal area A. Unless you have access to a wind tunnel, it is hard to measure Cd and A separately: instead, people often just measure or infer Cd A as a combined number The formula for the aerodynamic drag acting on a cyclist, in metric units, is: The formula for the aerodynamic drag acting on a cyclist, in metric units, is: Farag = 0.5-G-A-Rho-V2 The total force resisting you, the cyclist, is the sum of these three foroes: resist Fgravity + Frolling + Farag For each meter that you cycle forward, you spend energy overcoming this resistive force. The total amount of energy you must expend to move a distance D (m) against this force is called the Work (Joules) that you do: Work- Fresist If you are moving forward at velocity V (m/s), then you must supply energy at a rate that is sufficient to do the work to move V meters each second. This rate of energy expenditure is called power and it is measured in watts. The power Pwheel (watts) that must be provided to your bicyle's wheels to overcome the total resistive force Fresist (Newtons) while moving forward at velocity V (m/s) is: wheel retV You, the cyclist, are the engine providing this power. The power that must be provided to your bicycle's wheels comes from your legs, but not all of the power that your legs deliver make it to the wheels Friction n the drive train chains, gears, beanngs, etc.) causes a small amount of loss, usualy around 3%, assuming you have a dean and rice y ubicated drivetran Let's call the percentage of drivetain loss Lossdt (percent So, if the power that your legs provide is Piegs (watts), then the power that makes it to the wheel is: So, if the power that your legs provide is Plegs (watts), then the power that makes it to the wheel is: Loss ) negs , wheel = (1- Putting all together, the equation that relates the power produced by your logs to the steady-state speed you travel is -1 Loss Fgravity Frolling + Fdrag or, more fuly -1 Loss One of the scary implicasions of this equation is that at high speed, the power you have to produce is proportional to the cube of your velocity. So, to increase your speed by 25%, you need to nearly double your watage Part 2: Power you complete part 1, continue on to part 2 In part 2 you'll compute some more complex information about cyclying, including the power in watts that the cyclist needs to apply to the pedal to move at the velocity we calculated above. Sample session for part 2 (highlighted text means that the user has typed this information at the console): How steep is the hill you're climbing (%)? 3 How much do you weigh (in kg) 95 How much does your bike weigh (in kg) 7 What is your frontal area (in m*2)2 0.509 What is the windspeed (in km/h)? 20 What is the air density (in kg/m 3) 1.22 Grade of hill: 3.0% Rider weight: 95.0kg Bike weight: 7.0kg Frontal area of rider 0.509m 2 Windspeed: 20.0km/h Air density: 1.22kg/m 3 The rolling resistance for your bike is assumed to be 0.005 Your drag coefficient is assumed to be 0.63. your drive train loss is assumed to be 38. Force of gravity: 29.9950N Force of rolling resistance: 4.9992N Force of drag: 43.3094N Total force of reistance: 78.3036N Power applied to wheels: 730.1222w Power from your legs: 752.7033w Programmed by the Instructors Date: Thu Jan 17 11:59:46 2019 End of processing Explore the relationship between your cycling power (wattage) and speed. Move your cursor over the graph, or tap on it, to explore specific points. Modify the fields below and the graph will update 1000 Units: imperial metric Rider and bike parameters 500 Weight of rider (Ib) 165 Weight of bike (ib) T7 Total weight W (ib): 18200 Frontal area 54788 Drag coefficient Cd 0.63 Cd A (: 3.452 500 Drivetrain loss Lossdt(76) 3 1000 10 25 30 20 velocity (mph) Percent grade of hil G (negative for downhil) (%) 0 Speed of headwind (negative for talwind) (mph) Coetficient of rolling resistance Cr 0.00 Air density Rho (Ibtt) o076537 To maintain a velocity of 17.20 mph in these conditions, you must pedal with 124.24 watts of power Assistive forces You must pedal with 124.24 watts of power, after drivetrain loss of 3.73 watts, youll supply 20.51 watts to your wheel. Plegs " 12424w (10000%) Resistive forces Given groundspeed, a net headwind of 17.20 mph is working against you with 2.61 (bf) of force, or 89.38 watts of power Rolling resistance is working against you with 0.91 (lbf) of foroe, or 31.13 watts of power Drivetrain loss is costng you 37a watts of power Parag-8938m(7195%) Pollngesista 31.13w(25OS%) Panetarto",373m(300%) Solve for specific power or speed Iyou apply 200 watts of power, you will ride at velocity 20.73 mph. If you want to ride at velocity 22 mph, you must apply 23382 watts of power Solve for specific power or speed If you apply 200 watts of power, you will ride at velocity 20.73 mph. It you want to ride at velocity 22 mph, you must apply 233.82 watts of power The physics affecting cycling at constant speed This web page uses physical models of forces on a cyclist to help you estimate the relationship between power P (wats) and velocity V (kph or mph) of a cyclist. To do this, you need to estimate several parameters; reasonable defaults are given. There are three primary forces that you, as a cyclist, must overcome in order to move forward Gravity: If you're cycling uphil, youre fighting against gravity,but if you're cycling downhill, gravity works for you. This page measures the steepness of a hill in terms of percentage gradeG rise divided by run, mutipled by 100. The heavier you and your bike are, the more energy you must spend to overcome gravity. The combined weight of you (the cyclist) and your bike is W kg). The gravitational force constant g is 9.8067 (m/s) The formula for gravitational force acting on a cyclist, in metric units, is gravity = 9.S67 , sin(arctan( )-W Rolling resistance: Friction between your tires and the road surface slows you down. The bumpier the road, the more friction youll experience; the higher quality your tires and tube, the less friction youll experience. As well, the heavier you and your bike are, the more friction youll experience. There is a dimensionless parameter, called the coefficient of roling resistance, or C that captures the bumpiness of the road and the quality of your tres. The formula for the roilling resistance acting on a cyclist, in metric units, is Frolling-M8067 . cos(arctan( )) . w . c., Aerodynamic drag: As you cycle through the air, your bike and body need to push the air around you, similar to how a snowplow pushes snow out of the way Because of this, the air exerts a force against you as you ride. There are a few things that dictate how much force the air exerts against you. The faster you ride, velocity V (m/s), the more foroe the air pushes against you. As well, you and your bike present a cortain frontal aroa A (m2 to the air. The larger this frontal aroa, the more air you have to displace, and the larger the force the air pushes against you. This i why cyclists and bike manufacturers try hard to minimize frontal area in an aerodynamc position. The air density Rho (kg/m2) is also important: the more dense the air, the more force it exerts on you Finally, there are other effects, like the slipperyness of your clothing and the degree to which air flows laminarly rather than turbulentily around you and your bike. Optimizing your aerodynamic positions also help with this. These other effects are captured in another dimensionless parameter called the drag coolficient,or Co. Sometimes you will see people talking about Cd A,or CdA. This is just the drag coefficient Cd multiplied by the frontal area A. Unless you have access to a wind tunnel, it is hard to measure Cd and A separately: instead, people often just measure or infer Cd A as a combined number The formula for the aerodynamic drag acting on a cyclist, in metric units, is: The formula for the aerodynamic drag acting on a cyclist, in metric units, is: Farag = 0.5-G-A-Rho-V2 The total force resisting you, the cyclist, is the sum of these three foroes: resist Fgravity + Frolling + Farag For each meter that you cycle forward, you spend energy overcoming this resistive force. The total amount of energy you must expend to move a distance D (m) against this force is called the Work (Joules) that you do: Work- Fresist If you are moving forward at velocity V (m/s), then you must supply energy at a rate that is sufficient to do the work to move V meters each second. This rate of energy expenditure is called power and it is measured in watts. The power Pwheel (watts) that must be provided to your bicyle's wheels to overcome the total resistive force Fresist (Newtons) while moving forward at velocity V (m/s) is: wheel retV You, the cyclist, are the engine providing this power. The power that must be provided to your bicycle's wheels comes from your legs, but not all of the power that your legs deliver make it to the wheels Friction n the drive train chains, gears, beanngs, etc.) causes a small amount of loss, usualy around 3%, assuming you have a dean and rice y ubicated drivetran Let's call the percentage of drivetain loss Lossdt (percent So, if the power that your legs provide is Piegs (watts), then the power that makes it to the wheel is: So, if the power that your legs provide is Plegs (watts), then the power that makes it to the wheel is: Loss ) negs , wheel = (1- Putting all together, the equation that relates the power produced by your logs to the steady-state speed you travel is -1 Loss Fgravity Frolling + Fdrag or, more fuly -1 Loss One of the scary implicasions of this equation is that at high speed, the power you have to produce is proportional to the cube of your velocity. So, to increase your speed by 25%, you need to nearly double your watage