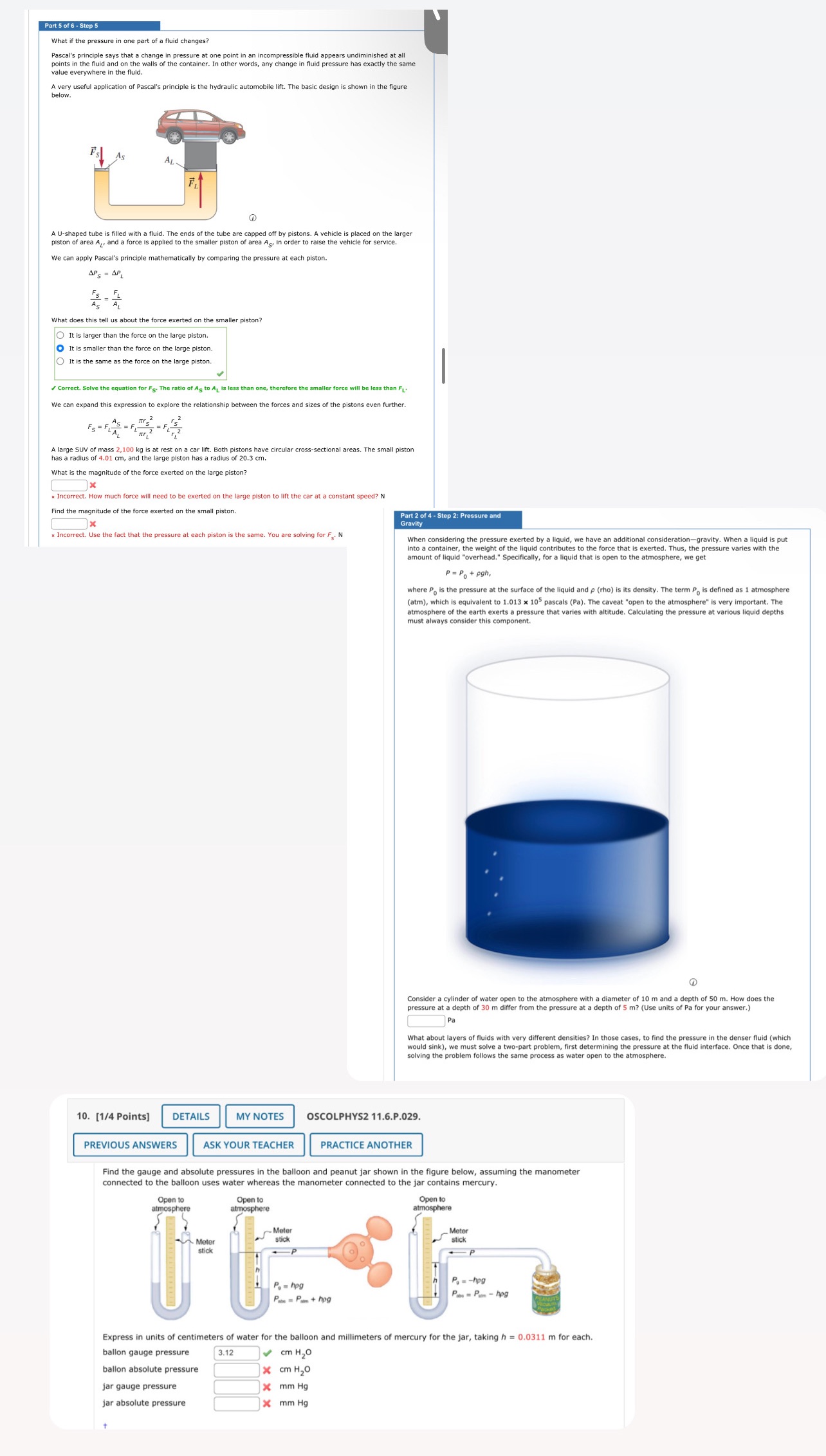
Part 5 of 6 - Step 5 What if the pressure one part of a fluid changes? Pascal's principle says that a change in pressure at one point in an incompressible fluid appears undiminished at all points in the fluid and on the walls of the container. In other words, any change in fluid pressure has exactly the same value everywhere in the fluid. A very useful application of Pascal's principle is the hydraulic automobile lift. The basic design is shown in the figure below. AL A U-shaped tube is filled with a fluid. The ends of the tube are capped off by pistons. A vehicle is placed on the larger piston of area A, and a force is applied to the smaller piston of area As, in order to raise the vehicle for service. We can apply Pascal's principle mathematically by comparing the pressure at each piston. APS - APL Fs FL As AL What does this tell us about the force exerted on the smaller piston? It is larger than the force on the large piston. It is smaller than the force on the large piston. O It is the same as the force on the large piston. Correct. Solve the equation for Fs. The ratio of As to A is less than one, therefore the smaller force will be less than FL. We can expand this expression to explore the relationship between the forces and sizes of the pistons even further. =F A large SUV of mass 2,100 kg is at rest on a car lift. Both pistons have circular cross-sectional areas. The small piston has a radius of 4.01 cm, and the large piston has a radius of 20.3 cm. What is the magnitude of the force exerted on the large piston? * Incorrect. How much force will need to be exerted on the large piston to lift the car at a constant speed? N Find the magnitude of the force exerted on the small piston. x Incorrect. Use the fact that the pressure t each piston is the same. You are solving for Fs. N Part 2 of 4-Step 2: Pressure and Gravity When considering the pressure exerted by a liquid, we have an additional consideration-gravity. When a liquid is put into a container, the weight of the liquid contributes to the force that is exerted. Thus, the pressure varies with the amount of liquid "overhead." Specifically, for a liquid that s open to the atmosphere, we get. P = Po + pgh, where Po is the pressure at the surface of the liquid and p (rho) its density. The term Po is defined as 1 atmosphere (atm), which is equivalent to 1.013 x 105 pascals (Pa). The caveat "open to the atmosphere" is very important. The atmosphere of the earth exerts a pressure that varies with altitude. Calculating the pressure at various liquid depths must always consider this component. Consider a cylinder of water open to the atmosphere with diameter of 10 m and a depth of 50 m. How does the pressure at a depth of 30 m differ from the pressure at a depth of 5 m? (Use units of Pa for your answer.) Pa What about layers of fluids with very different densities? In those cases, to find the pressure in the denser fluid (which would sink), we must solve a two-part problem, first determining the pressure at the fluid interface. Once that is done, solving the problem follows the same process as water open to the atmosphere. 10. [1/4 Points] DETAILS MY NOTES OSCOLPHYS2 11.6.P.029. PREVIOUS ANSWERS ASK YOUR TEACHER PRACTICE ANOTHER Find the gauge and absolute pressures in the balloon and peanut jar shown in the figure below, assuming the manometer connected to the balloon uses water whereas the manometer connected to the jar contains mercury. Open to atmosphere Meter stick Open to atmosphere Meter stick Open to atmosphere Meter stick P-hpg Pabe Pam+hog P=-hog PP-hog Express in units of centimeters of water for the balloon and millimeters of mercury for the jar, taking h=0.0311 m for each. ballon gauge pressure 3.12 20 ballon absolute pressure x cm HO jar gauge pressure x mm Hg jar absolute pressure X mm Hg. +