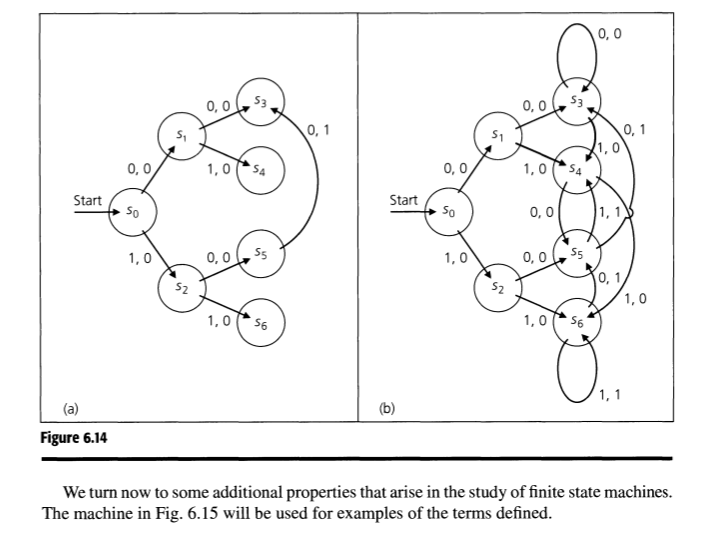
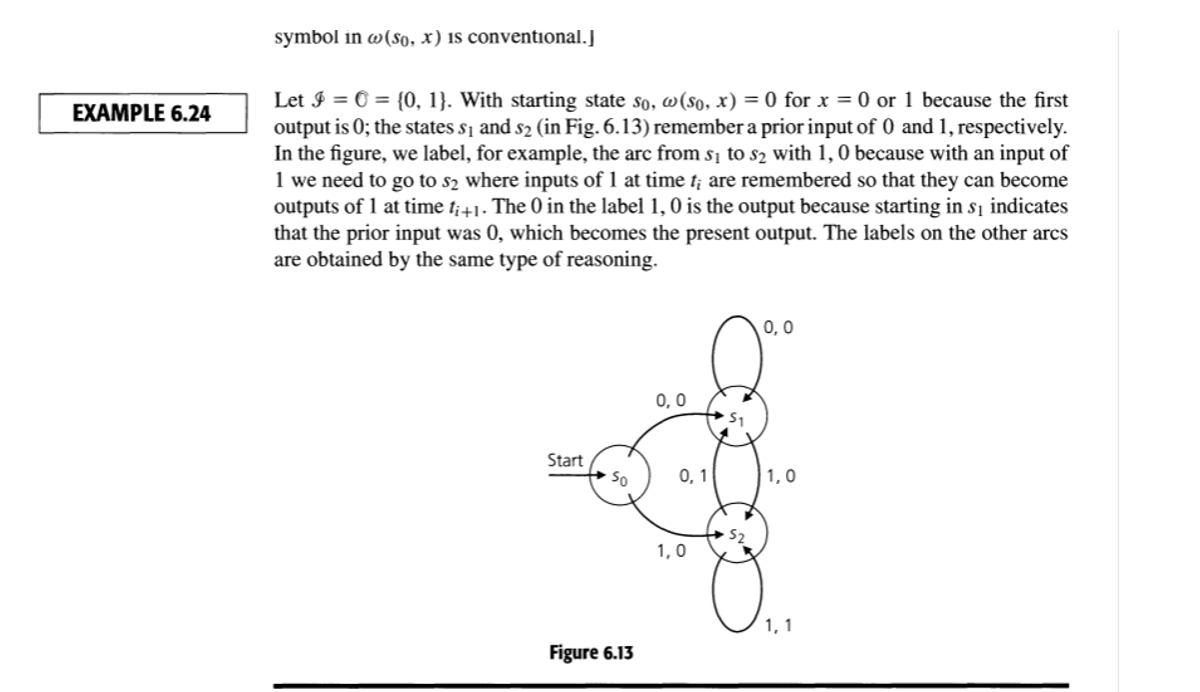
Part A: In example 6.24, figure 6.13, we are presented with a 1-unit delay machine. It has 3 states. In example 6.25, figure 6.14(b), we have a 2-unit delay machine. It has 7 states.
\f\f0, 0 0, 0 53 0, 0 53 51 0, 1 51 0, 1 X1, O 0, 0 1, 0 0, 0 1, 0 Start Start $ 50 0, 0 1, 1 1, 0 0, 0 $5 1,0 0, 0 55 0. 1 52 52 1, 0 1, 0 56 1, 0 56 1, 1 (a) (b) Figure 6.14 We turn now to some additional properties that arise in the study of finite state machines. The machine in Fig. 6.15 will be used for examples of the terms defined.Part C: Give a recursive definition for the language A over {0, 1} containing exactly all of the binary strings in which 00 is never a substring. For example, A contains the strings 0, 1, 01, 10, 111, 011, 110, 101, and so on. Use examples 6.14 and 6.15 to guide you. Be sure to test your definition thoroughly. As we close this first section we further examine the idea of a recursively defined set (given in Section 4.2), as demonstrated in the following three examples. EXAMPLE 6.14 For the alphabet E = (0, 1} consider the language A C E* where each word in A contains exactly one occurrence of the symbol 0. Then A is an infinite set, and among the words in A one finds 0, 01, 10, 01111, 11110111, and 11111111110. There are also infinitely many words in E* that are not in A - such as, 1, 11, 00, 000, 010, and 011111111110. We can define this language A recursively as follows: 1) Our base step tells us that O e A; and 2) For the recursive process we want to include in A the words 1x and x 1, for each word X EA. Using this definition, the following discussion shows us that the word 1011 is in A. From part (1) of our definition, we know that 0 E A. Then by applying part (2) of our definition - three times - we find: i) 01 E A, because O E A; ii) 011 E A, because 01 E A; and i) Since 011 E A, we have 1011 E A. EXAMPLE 6.15 For E = ((,))- the alphabet containing the left and right parentheses - we want to con- sider the language A C E* consisting of those nonempty strings of parentheses that are grammatically correct for algebraic expressions. Hence we find, for example, the three strings (( )), ((() ())), and ( ) ( ) () in this language, but we do not find strings such as (OO, 0) ((), or )( )(())). We see that if a string x(# A) is to be in A, then i) we must have the same number of left parentheses in x as there are right parentheses; and ii) the number of left parentheses must (always) be greater than or equal to the number of right parentheses, as we examine each of the parentheses in x -reading them consecutively from left to right. The language A may be given recursively as follows: 1) () is in A; and 2) For all x, y E A we have (i) xy E A and (ii) (x) E A. [As we mentioned prior to Example 4.22, we also have an implicit restriction here - that no string of parentheses is in A unless it can be derived through steps (1) and (2) above.] Using this recursive definition, the following shows us how to establish that the string (()()) in E* is in the language A. Steps Reasons 1) () is in A. Part (1) of the recursive definition 2) ( )() is in A. Step (1) and part (2i) of the definition 3) (()()) is in A. Step (2) and part (2ii) of the definitionsymbol in w(So, x) is conventional. ] EXAMPLE 6.24 Let $ = 0 = (0, 1). With starting state so, w(so, x) = 0 for x = 0 or 1 because the first output is 0; the states s, and $2 (in Fig. 6.13) remember a prior input of 0 and 1, respectively. In the figure, we label, for example, the arc from s, to $2 with 1, 0 because with an input of 1 we need to go to $2 where inputs of 1 at time , are remembered so that they can become outputs of 1 at time fi+1 . The 0 in the label 1, 0 is the output because starting in $1 indicates that the prior input was 0, which becomes the present output. The labels on the other arcs are obtained by the same type of reasoning. 0, 0 0, 0 Start so 0, 1 1,0 1, 0 1, Figure 6.13EXAMPLE 6.25 Observing the structure of a one-unit delay. we extend our ideas to the two-unit delay machine shown in Fig. 6.14. Ifx E 5'.1etx = xlxg - - - x," wherem > 2; ifs-o is the starting state, then who. x) = (Din - - - x..-2. For states so, 51, 52 the output is 0 for all possible inputs. States 53. s... 55. and 5'6 must remember the two prior inputs 00, 01, 10, and 11, respectively. To get the other arts in the diagram. we shall consider one such are and then use similar reasoning for the others. For the are from 55 to s; in Fig. 6.l4{a). let the input be 0. Since the prior input to 55 from s; is 0, we must go to the state that remembers the two prior inputs 00. This is state 53. Going back two states from 35 to s: to so. we see that the input is I (from So to 52). This then becomes the output (delayed two units) for the are from 35 to 53. The complete machine is shown in part (b) of Fig. 6.14. 12. For E = {0, 1} determine whether the string 00010 is in each of the following languages (taken from E'). a) {0,1}* b) {000, 101}{10,11} c) {00}{0}'{10} d) {000}'{l}*{0} e) {00}*{10}' 1') {0}*{1}*{0}"