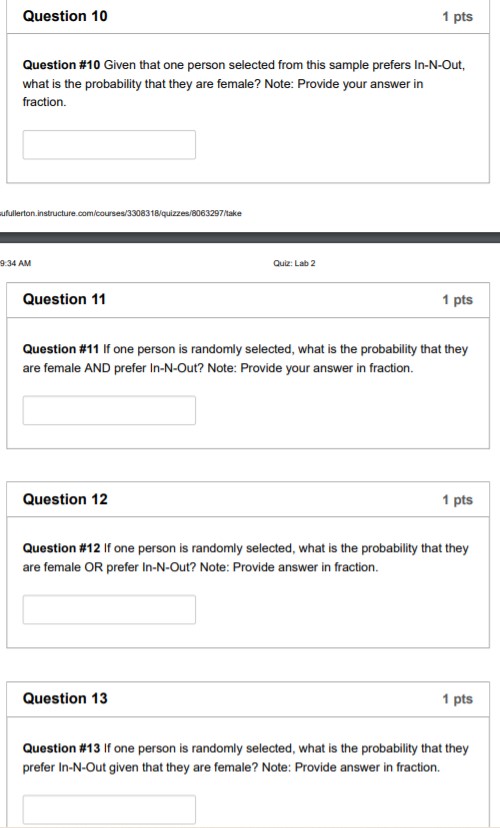
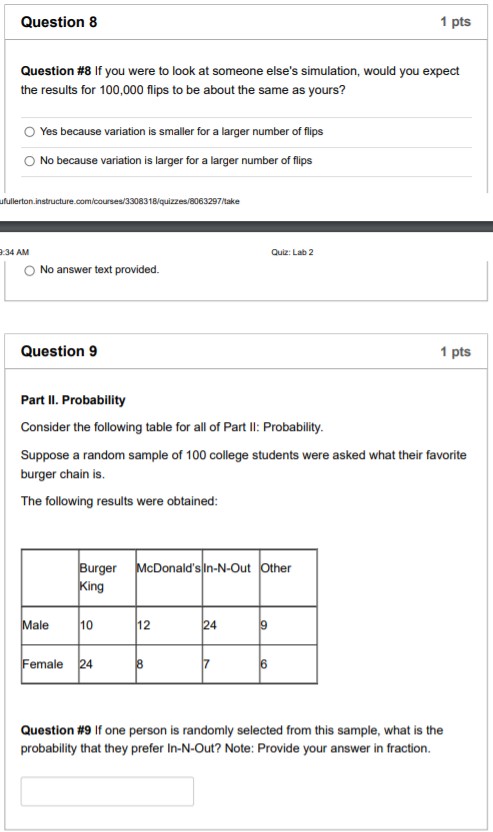
Part I. Relative Frequency Suppose a random experiment is repeated many times, for example, a fair coin is ipped 1000 times. The outcome from a single flip of the coin is either Heads or Tails. If we repeat the experiment, the number of times each outcome is observed, i.e., the number of Heads and the number of Tails, is called the frequency of that outcome. The relative frequency of an outcome is the proportion of times that outcome is observed. For example, the relative frequency of Heads is the frequency of heads divided by the total number of ips (this was the fraction that we computed in class in the quarter ipping experiment last Thursday). By the Law of Large Numbers. as the number of repetitions of an experiment increases, the relative frequency of each outcome approaches the probability of that outcome. In this lab you will use computer simulation to nd the relative frequency of an outcome and to show how. as the number of repetitions of the experiment increases, the relative frequency stabilizes to a number between 0 and 1. Since we have already demonstrated coin ips. let's look at a scenario of rolling a die and our outcome of interest (event of interest) is rolling a 6. In order to do this in RStudio, we need to specify the sample space and the probability associated with each outcome. Question #1 What is the sample space, S, of rolling a regular 6-sided die? Note: In your solution separate each number with a comma. O {1, 2, 3, 4, 5, 6} O {(1,1),(1,2),...,(6,5),(6,6)} O {1, 2} O {2,3,4,5,6,7,8,9,10, 11,12} fullerton.instructure.com/courses/3308318/quizzes/8063297/take 34 AM Quiz: Lab 2 Question 2 1 pts Question #2 What is the probability (in fraction form) associated with each outcome?Question 3 1.5 pts In RSudio, specify your sample space in a vector and create a corresponding vector of the associated probabilities: :1 s = c(1, 2, 3, :1, 5, 5) > Prob = 511:5, 1:5,1:5, 1:5, 1:5, 1:5) Now, let's simulate rolling the die 10 times by randomly sampling a value of the sample space with probability specied in our probability vector: :- Roll.1ti = sample(x = 3, size = 10, prob = Prob, replace = TRUE) ##note that by setting replace equal to TRUE, this replaces the value we just sampled, thus making each experiment repetition INDEPENDENT. :1 R0ll.10 Question #3 How would you calculate the relative frequency of the number 6 in your "Rol|.10" vector? 0 Count the number of 6's and divide by 10 O Count the number of 6's and divide by the sum of the 10 rolls 0 Add the number of 6's together and divide by the sum of the 10 rolls 0 No answer text provided. \fQuestion 5 0 pts We want to observe the law of large numbers taking effect by increasing the number of times we "roll the die". Redo your simulation for each of the following number of rolls (note this just requires you to change the size in the previous RStudio code): 10, 100, 1000, 10000, 100000. To make your life easy, let's use the count() function to give us the total number of 6's in each simulation (unless you want to count the number of 6's by hand...which I would not recommend). This function is in a special library that we have to install and load. Enter the following commands in RStudio: > install.packages('plyr") > library(plyr) > count(Roll.10) #should pop up a frequency table in RStudio giving you directly the number of 6's out of 10 rolls. Question #5 Fill in table below with your results: You may simply list your proportions in the order of the rows in your answer. Number of Rolls Relative Frequency (Proportion of 6's) 10 100 1000 10000 100000Question 6 1.5 pts Question #6 As the number of rolls increases from 10 to 100000, describe what happens to the relative frequency of the occurrence of observing a 6. O Converges to 1/6 O Diverges from 1/6 O Nothing changes Question 7 1 pts Question #7 If you were to look at someone else's simulation, would you expect the results for 10 flips to be about the same as yours? No because there is more variation in a smaller number of flips Yes because there is less variation in a smaller number of flips Yes because there is a pattern in the short runQuestion 8 1 pts Question #8 If you were to look at someone else's simulation, would you expect the results for 100,000 flips to be about the same as yours? O Yes because variation is smaller for a larger number of flips O No because variation is larger for a larger number of flips ifullerton.instructure.com/courses/3308318/quizzes/8063297/lake 1:34 AM Quiz: Lab 2 O No answer text provided. Question 9 1 pts Part II. Probability Consider the following table for all of Part II: Probability. Suppose a random sample of 100 college students were asked what their favorite burger chain is. The following results were obtained: Burger McDonald's In-N-Out Other King Male 10 12 24 9 Female 24 8 7 6 Question #9 If one person is randomly selected from this sample, what is the probability that they prefer In-N-Out? Note: Provide your answer in fraction.Question 10 1 pts Question #10 Given that one person selected from this sample prefers In-N-Out, what is the probability that they are female? Note: Provide your answer in fraction. ufullerton.instructure.com/courses/3308318/quizzes/8063297/lake 9:34 AM Quiz: Lab 2 Question 11 1 pts Question #11 If one person is randomly selected, what is the probability that they are female AND prefer In-N-Out? Note: Provide your answer in fraction. Question 12 1 pts Question #12 If one person is randomly selected, what is the probability that they are female OR prefer In-N-Out? Note: Provide answer in fraction. Question 13 1 pts Question #13 If one person is randomly selected, what is the probability that they prefer In-N-Out given that they are female? Note: Provide answer in fraction