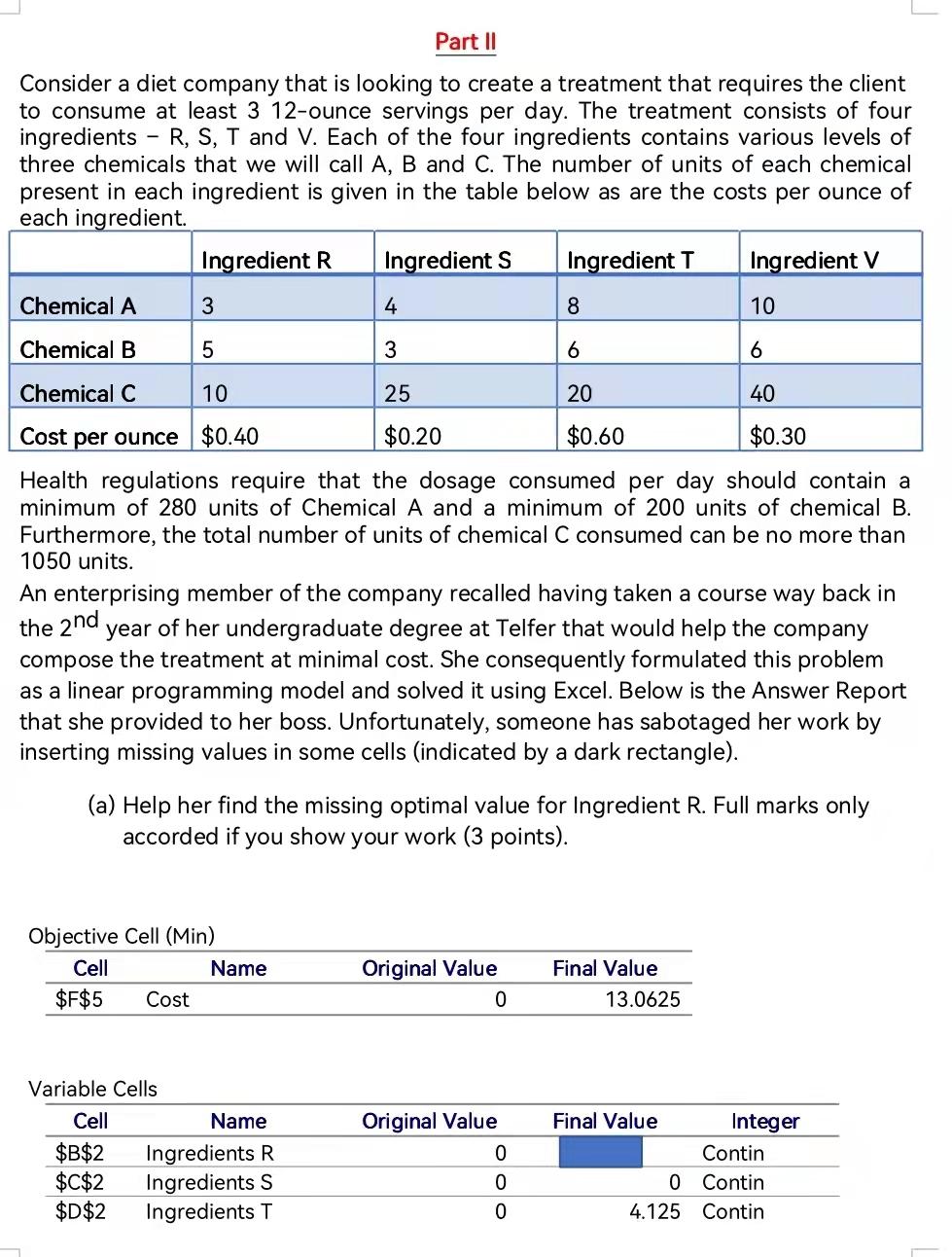
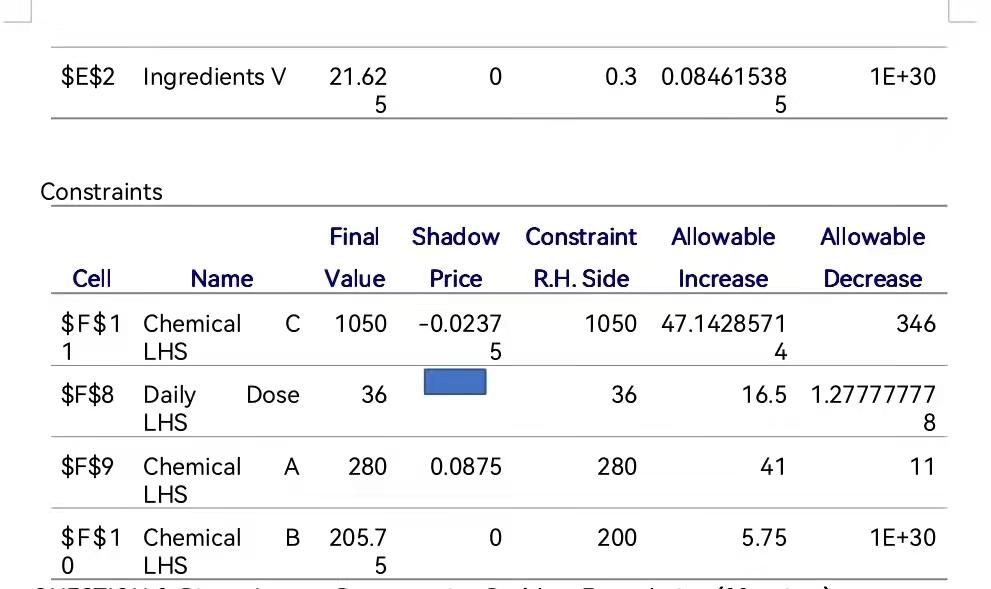
Part II Consider a diet company that is looking to create a treatment that requires the client to consume at least 3 12-ounce servings per day. The treatment consists of four ingredients - R, S, T and V. Each of the four ingredients contains various levels of three chemicals that we will call A, B and C. The number of units of each chemical present in each ingredient is given in the table below as are the costs per ounce of each ingredient. Ingredient R Ingredients Ingredient T Ingredient v Chemical A 3 4 8 10 Chemical B 5 3 6 6 Chemical C 10 25 20 40 Cost per ounce $0.40 $0.20 $0.60 $0.30 Health regulations require that the dosage consumed per day should contain a minimum of 280 units of Chemical A and a minimum of 200 units of chemical B. Furthermore, the total number of units of chemical C consumed can be no more than 1050 units. An enterprising member of the company recalled having taken a course way back in the 2nd year of her undergraduate degree at Telfer that would help the company compose the treatment at minimal cost. She consequently formulated this problem as a linear programming model and solved it using Excel. Below is the Answer Report that she provided to her boss. Unfortunately, someone has sabotaged her work by inserting missing values in some cells (indicated by a dark rectangle). (a) Help her find the missing optimal value for Ingredient R. Full marks only accorded if you show your work (3 points). Objective Cell (Min) Cell Name $F$5 Cost Original Value 0 Final Value 13.0625 Original Value Variable Cells Cell Name $B$2 Ingredients R $C$2 Ingredients S $D$2 Ingredients T Ooo Final Value Integer Contin 0 Contin 4.125 Contin $E$2 Ingredients V 0 21.625 Contin b) What would happen to the optimal solution and the optimal objective value if the limit on Chemical B was increased to 203? (3 points) c) As a follow-up her bosses asked her a number of questions which she answered using the sensitivity report given below. Provide your answers to the questions along with justification. i. What is the impact on the optimal value of the objective function if the treatment must contain 2 ounces of ingredient S (round to two decimal points)? (3 points) ii. There is some concern that the cost of an ounce of ingredient I may T jump to $2.00. What is the impact on the optimal solution as well as the optimal objective function value? Make sure to justify your answer. (4 points) iii. Previously, an enterprising former Telfer student had solved the same problem but for a daily dosage of 46 ounces. He had determined an optimal cost of 16.81. Use this to determine the impact on increasing the daily dosage to 50. (5 points) Hint: calculate the shadow price for the Daily Dos Variable Cells Final Objective Allowable Reduce d Allowable Cell Name Value Cost Increase Decrease Coefficien t $B$2 Ingredients R 10.25 0 0.25 0.4 0.06111111 1 0 0.06875 0.2 1E+30 0.06875 $C$2 Ingredients S $D$2 Ingredients T 4.125 0 0.6 1.5 0.07333333 3 $E$2 Ingredients V 0 1E+30 21.62 5 0.3 0.08461538 5 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease 1050 346 $F$1 Chemical 1 LHS -0.0237 5 1050 47.1428571 4 Dose 36 36 $F$8 Daily LHS 16.5 1.27777777 8 A 280 0.0875 280 41 11 $F$9 Chemical LHS B 0 200 5.75 1E+30 $F$1 Chemical 0 LHS 205.7 5 Part II Consider a diet company that is looking to create a treatment that requires the client to consume at least 3 12-ounce servings per day. The treatment consists of four ingredients - R, S, T and V. Each of the four ingredients contains various levels of three chemicals that we will call A, B and C. The number of units of each chemical present in each ingredient is given in the table below as are the costs per ounce of each ingredient. Ingredient R Ingredients Ingredient T Ingredient v Chemical A 3 4 8 10 Chemical B 5 3 6 6 Chemical C 10 25 20 40 Cost per ounce $0.40 $0.20 $0.60 $0.30 Health regulations require that the dosage consumed per day should contain a minimum of 280 units of Chemical A and a minimum of 200 units of chemical B. Furthermore, the total number of units of chemical C consumed can be no more than 1050 units. An enterprising member of the company recalled having taken a course way back in the 2nd year of her undergraduate degree at Telfer that would help the company compose the treatment at minimal cost. She consequently formulated this problem as a linear programming model and solved it using Excel. Below is the Answer Report that she provided to her boss. Unfortunately, someone has sabotaged her work by inserting missing values in some cells (indicated by a dark rectangle). (a) Help her find the missing optimal value for Ingredient R. Full marks only accorded if you show your work (3 points). Objective Cell (Min) Cell Name $F$5 Cost Original Value 0 Final Value 13.0625 Original Value Variable Cells Cell Name $B$2 Ingredients R $C$2 Ingredients S $D$2 Ingredients T Ooo Final Value Integer Contin 0 Contin 4.125 Contin $E$2 Ingredients V 0 21.625 Contin b) What would happen to the optimal solution and the optimal objective value if the limit on Chemical B was increased to 203? (3 points) c) As a follow-up her bosses asked her a number of questions which she answered using the sensitivity report given below. Provide your answers to the questions along with justification. i. What is the impact on the optimal value of the objective function if the treatment must contain 2 ounces of ingredient S (round to two decimal points)? (3 points) ii. There is some concern that the cost of an ounce of ingredient I may T jump to $2.00. What is the impact on the optimal solution as well as the optimal objective function value? Make sure to justify your answer. (4 points) iii. Previously, an enterprising former Telfer student had solved the same problem but for a daily dosage of 46 ounces. He had determined an optimal cost of 16.81. Use this to determine the impact on increasing the daily dosage to 50. (5 points) Hint: calculate the shadow price for the Daily Dos Variable Cells Final Objective Allowable Reduce d Allowable Cell Name Value Cost Increase Decrease Coefficien t $B$2 Ingredients R 10.25 0 0.25 0.4 0.06111111 1 0 0.06875 0.2 1E+30 0.06875 $C$2 Ingredients S $D$2 Ingredients T 4.125 0 0.6 1.5 0.07333333 3 $E$2 Ingredients V 0 1E+30 21.62 5 0.3 0.08461538 5 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease 1050 346 $F$1 Chemical 1 LHS -0.0237 5 1050 47.1428571 4 Dose 36 36 $F$8 Daily LHS 16.5 1.27777777 8 A 280 0.0875 280 41 11 $F$9 Chemical LHS B 0 200 5.75 1E+30 $F$1 Chemical 0 LHS 205.7 5