PAST CASE STUDY, THIS IS JUST IN CASE IF NEEDED:

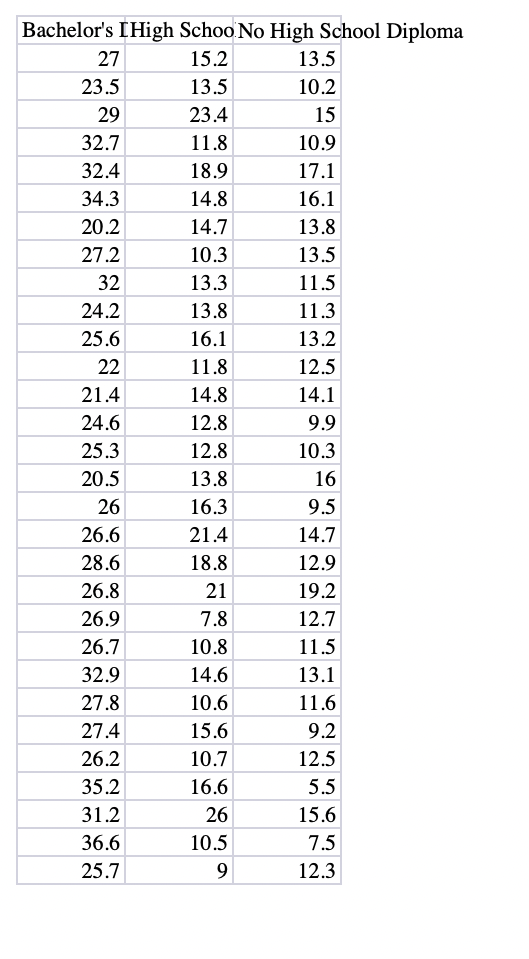
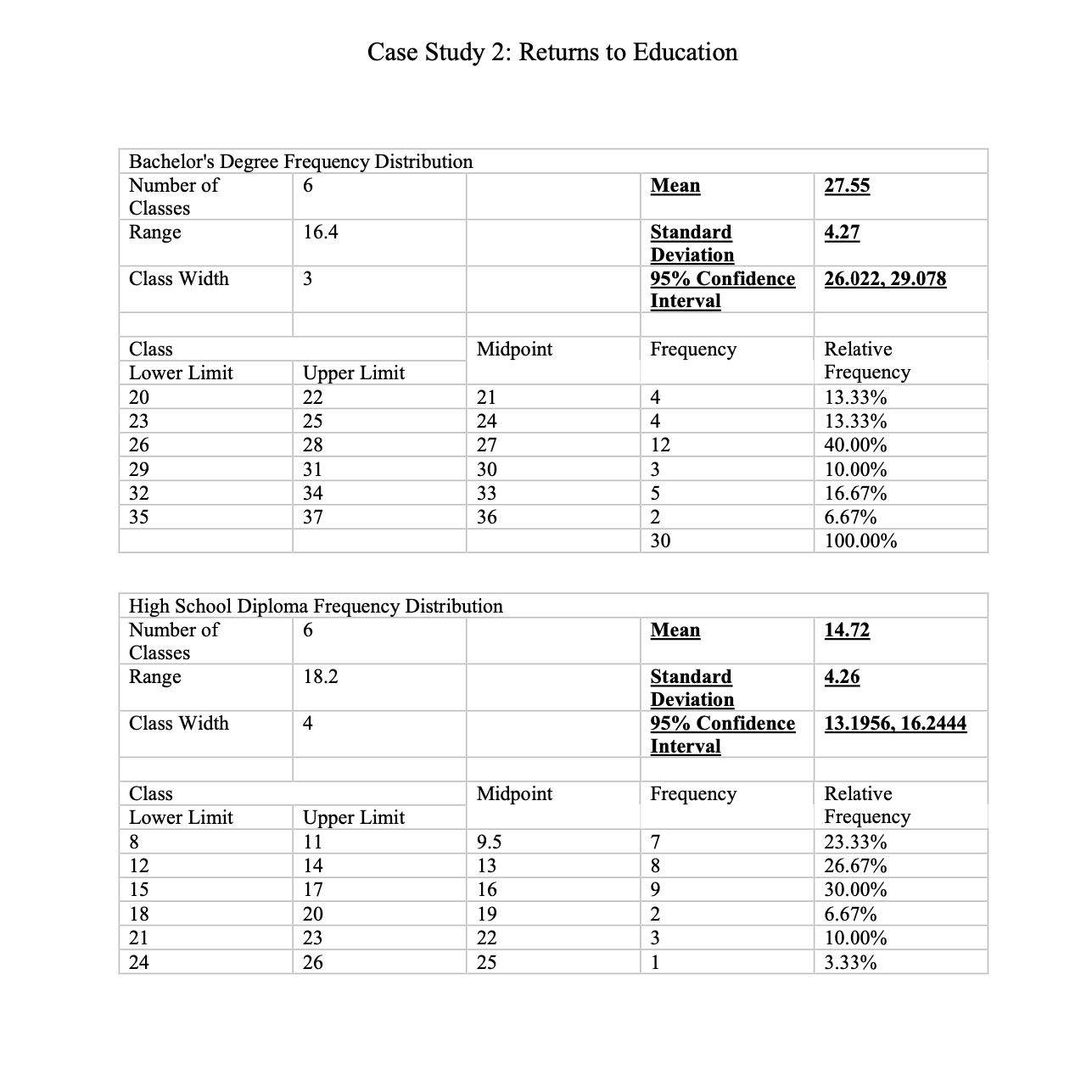
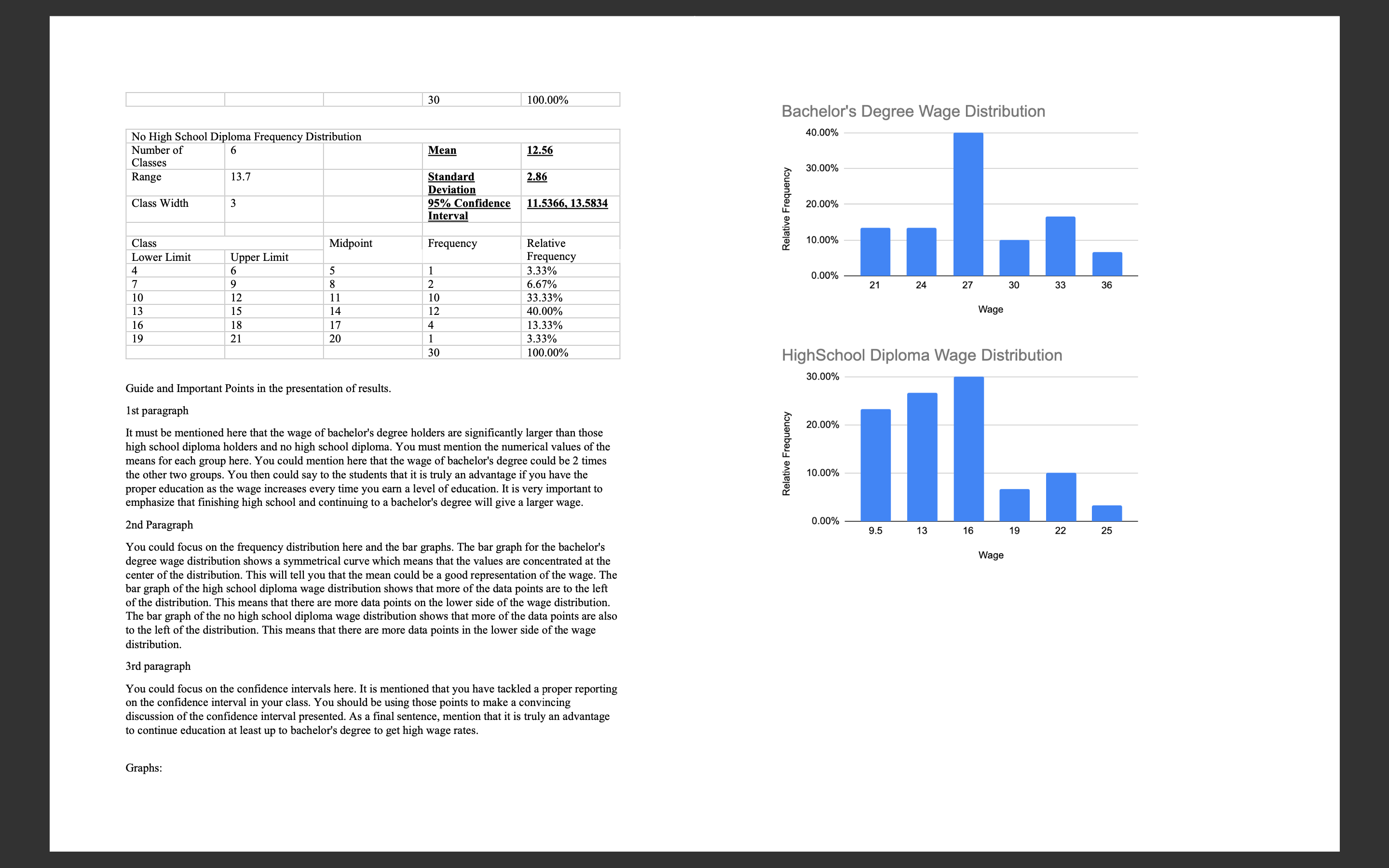
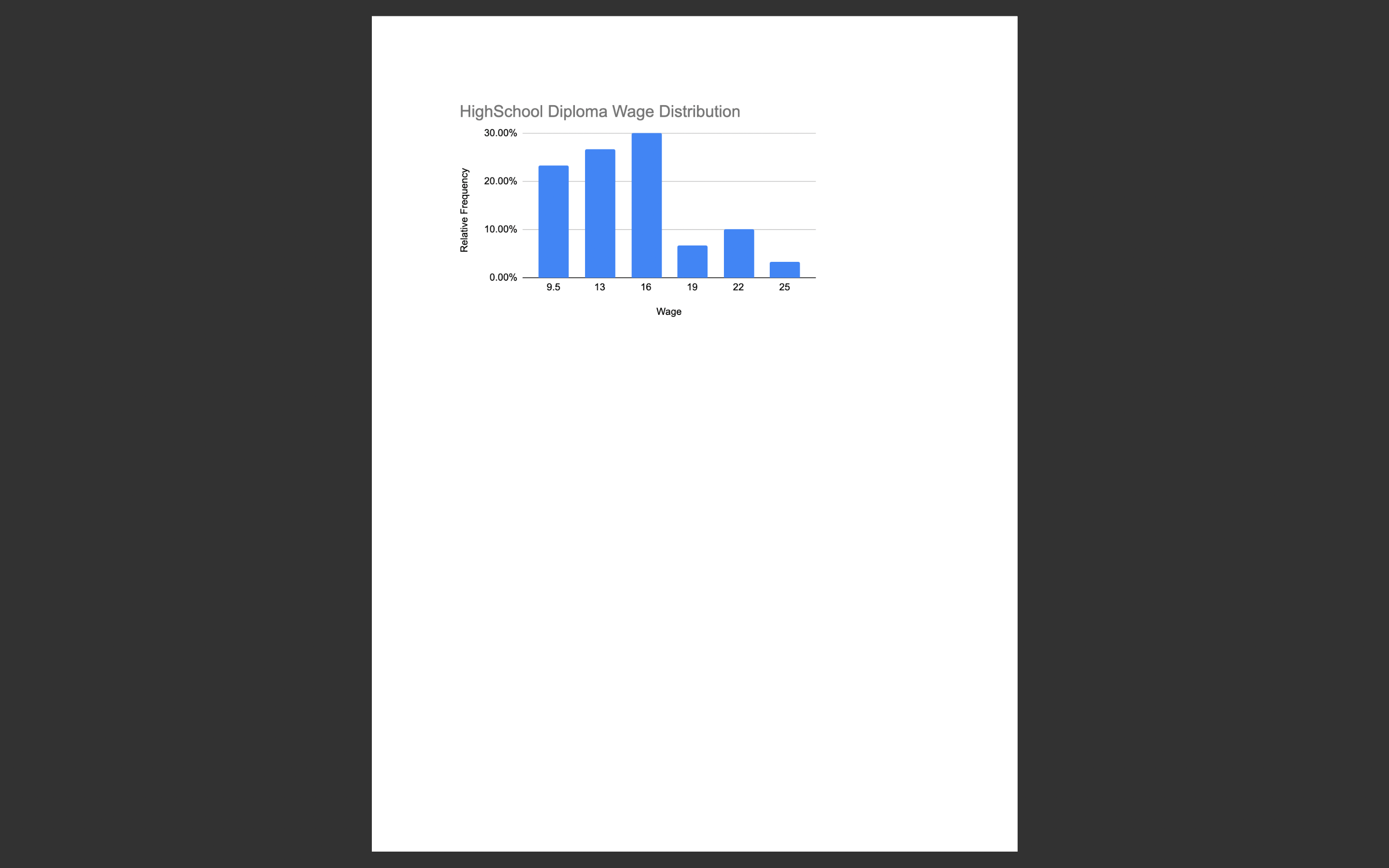
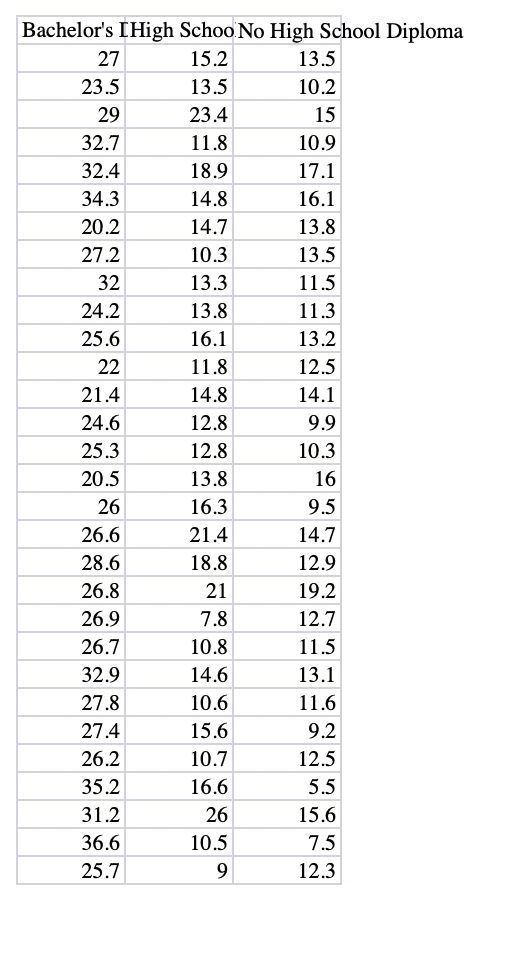
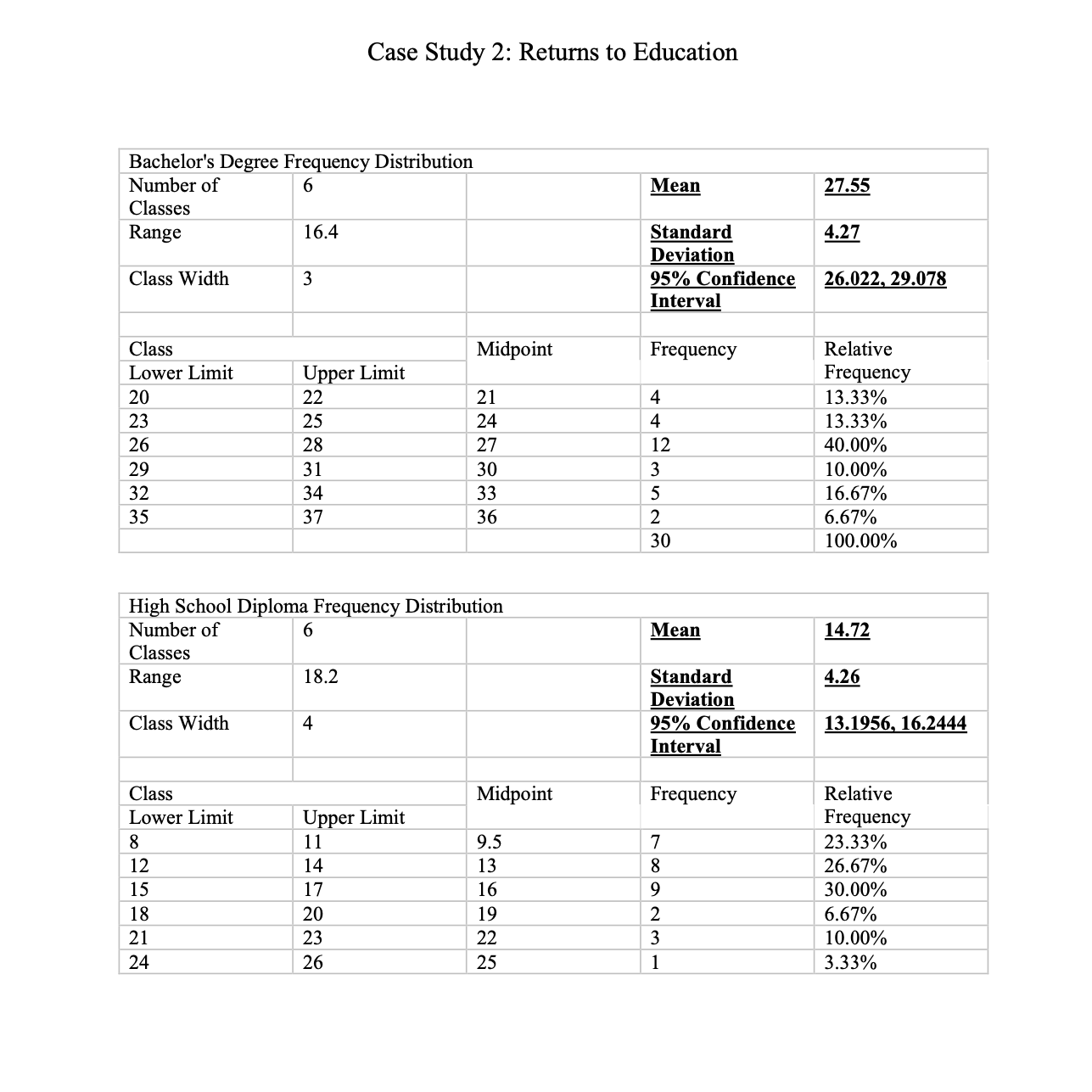
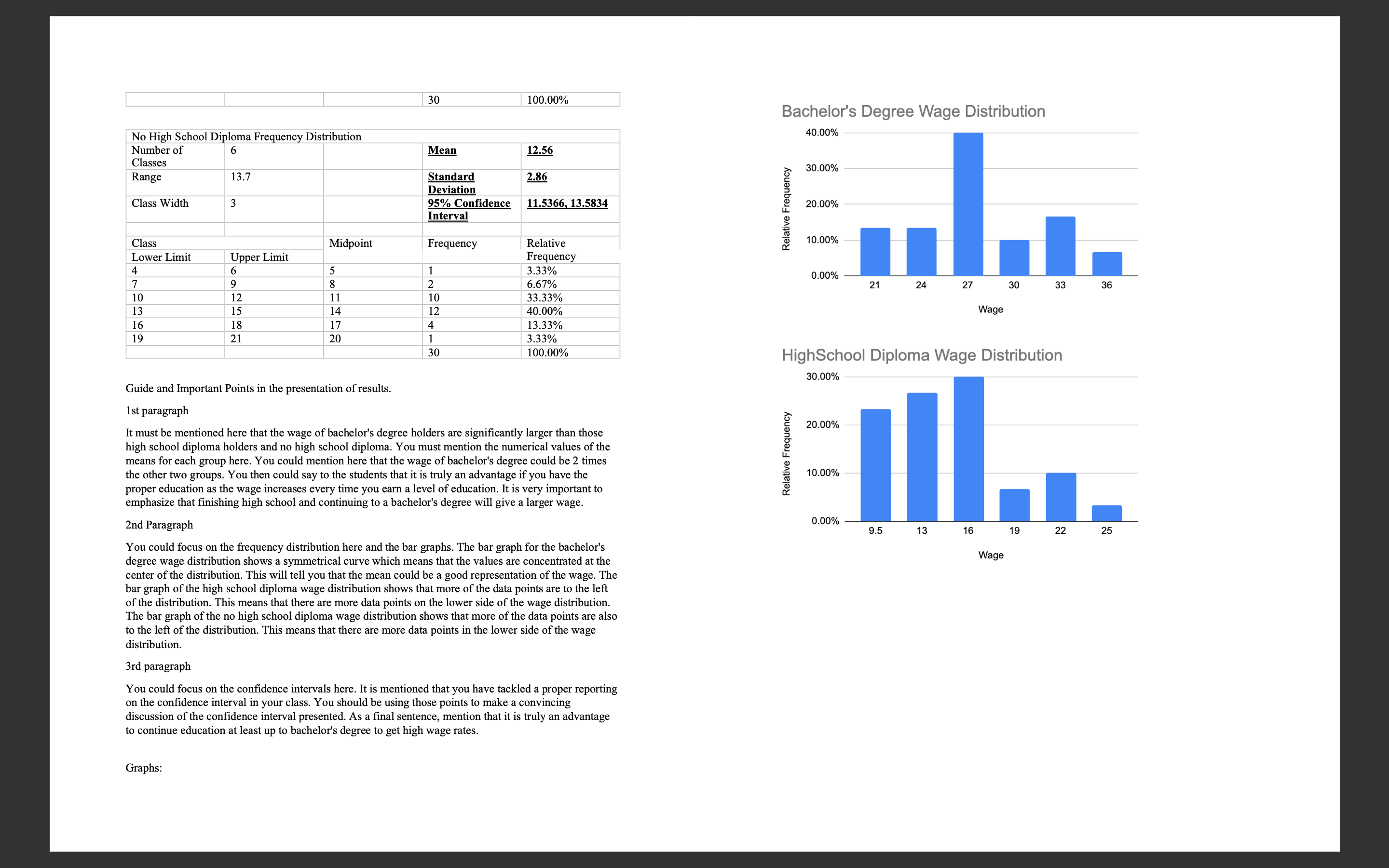
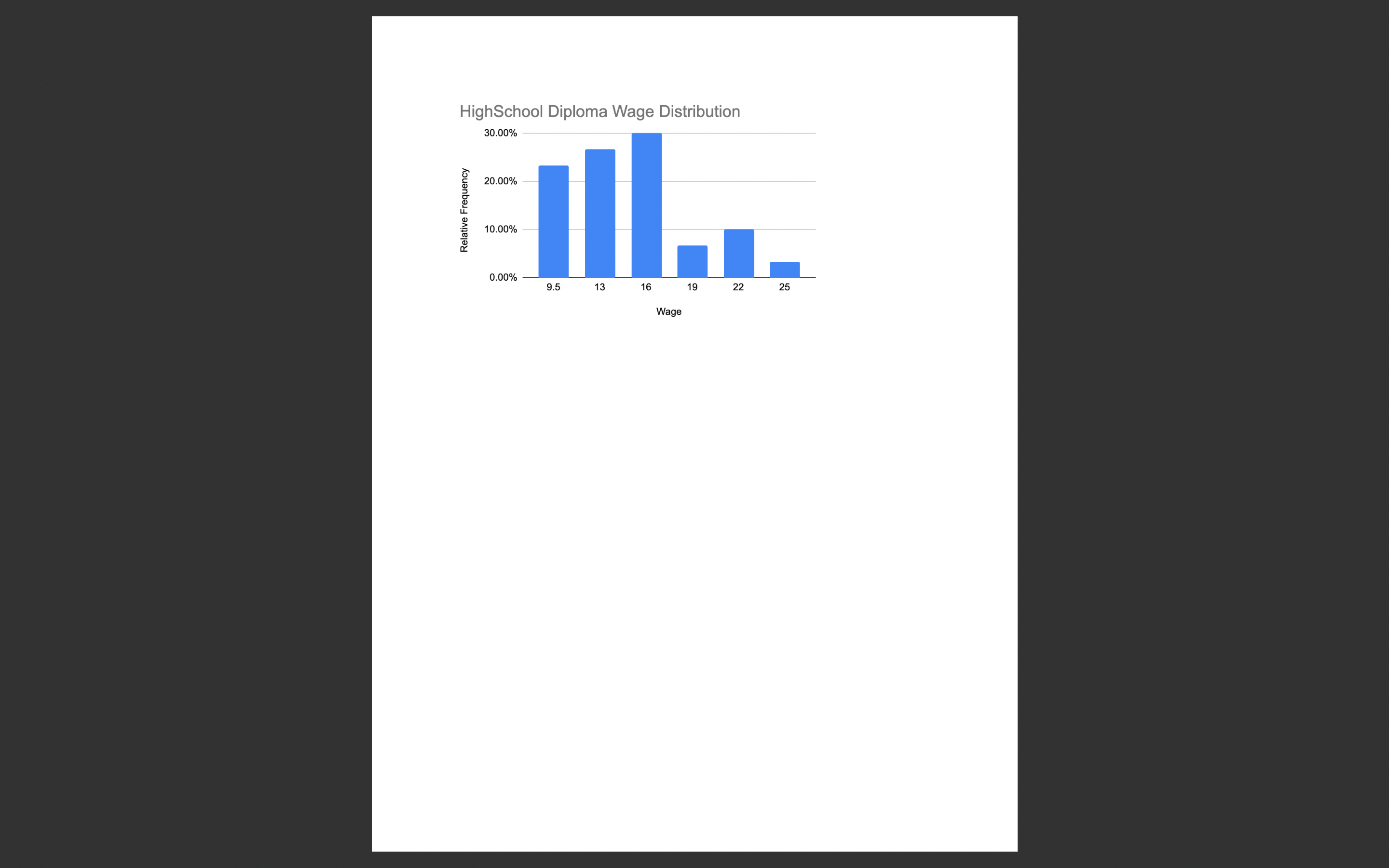
\fFor this case study, we are going to continue with the data that we used for Case Study 2. When you did the last study, you had learned to create condence intervals but you had not yet learned hypothesis testing. The condence interval allowed us to form some expectations about the population mean of wages for workers with bachelor's and high school degrees, and also for workers who do not have a high school diploma. Most of you, at the time, just used the sample means to try to argue that the workers with a bachelor's will be paid more than the ones with only a high school diploma and the latter will be paid more than workers with no high school diploma. This is not a compelling argument because the sample mean is just looking at 30 people in the population and we cannot assume that the mean of our sample is the same at the unknown population mean that we are trying to estimate. Which is why we used the sample mean to construct condence intervals with some margin of error to claim that we are pretty condent that the unknown population mean is somewhere within the wage interval that we calculated (please go back and review the feedback I provided after the last case study; also attached here for your convenience i). Again, as in the previous case, suppose you are a career advisor at a high school and you want to make a presentation to students who are just starting high school. Prior to the presentation, you are going to compile and share a report with the students. You have some data on waggn dollars i) received by people with No High School, a High School Diploma and a Bachelor's Degree. You will use these data to write a report which analyzes the advantages of different levels of education in terms of average wages received. Many of you did not create meaningful frequency tables and histograms to summarize and present the data. I am going to reserve 10 points from this study for a second attempt to do the same: please make a frequency table similar to the one in the attached feedback from the previous case study; so, no more than 5 bins (wage intervals) for the data, clearly labelled; and the accompanying histogram with wage intervals on the x-axis and relative frequencies on the y-axis. Please go back to Chapter 2 if you nd this still confusing. And please do not include line graphs or scatterplots of all the data observations. When doing your data analysis, please set up and test the following hypotheses: 1. The population mean wage for workers with high school diplomas is greater than the population mean wage for workers who do not have a high school diploma. 2. The population mean wage for workers with high school diplomas is more than $2 higher than the population mean wage for workers who do not have a high school diploma. 3. The population mean wage for workers with high school diplomas is more than $1 higher than the population mean wage for workers who do not have a high school diploma. 4. The population mean wage for workers with a bachelor's degree is greater than the population mean wage for workers with a only high school diploma. 5. The population mean wage for workers with a bachelor's degree is more than $10 higher than the population mean wage for workers with only a high school diploma. 6. The population mean wage for workers with a bachelor's degree is more than $9 higher than the population mean wage for workers with only a high school diploma. For ease of comparison, assume xbar1 is the sample mean wage for workers with a high school diploma; xbar2 is the sample mean wage for workers with no high school diploma; and xbar3 is the sample mean wage for workers with a bachelor's degree. Hint: when testing whether one population mean is bigger that the other, use the bigger mean first in calculating the difference. For example, when testing if mean wage for workers with a bachelor's degree is bigger than the mean wage for high school, use (xbar3 minus xbar1). For each of the hypothesis tests, please note: 1. We cannot assume that the unknown population variances are equal. 2. Implement the tests at the 5% significance level. 3. Please use the p-value approach to test each hypothesis. Please refer to "10.4: Writing with Data" at the end of Chapter 10 and use the table format provided there to show your hypothesis, your test statistic and the corresponding.p-value. Please note the table not only shows the formula, but shows the numbers you plugged into the formula as well as if you are using a t or a z statistic. At least 20 points will be deducted if you do not use this table format to share your test results. 4. Please write about three paragraphs to interpret the data, and to summarize the main findings. Please address your writing to your high school student audience. Your writing should be clearly related to the above table you have created to summarize the results of your hypothesis tests.Many people had trouble explaining why they were creating confidence intervals and how to interpret these confidence intervals and use them to make their case to their audience. Although the average wage for each level of education is different, you have to ask yourself what is the added information that making the confidence intervals gives you beyond just the mean wage that we calculated for each of the categories. For example, you can say to the students: "As you can see, the mean wage for workers with a bachelor's degree is $27.55 versus $14.72 for workers with a high school diploma and only $12.25 for workers with no high school diploma. But we just calculated each of these by taking a sample of only 30 workers. Maybe, there was something peculiar about the samples we did take; maybe these averages do not accurately reflect what the true average wage for each of these categories really is in the larger workforce? In order to get more clarity on these estimates, we are going to use confidence intervals. Table gives you 95% confidence intervals for each of the three categories of education. As you can see, the confidence interval for the mean wage for a bachelor's degree is $25.95 to $29.14. Here is the interpretation: we can claim that this particular confidence interval that we created using this particular sample mean has a 95% chance of capturing the (fixed but unknown) true population mean; it is telling us something about what our population mean might be, but we are not 100% sure; we are only 95% sure. Another way to say this is that, based on our sample of mean, we are 95% confident that the true average wage for workers with a bachelor's degree in the population is somewhere between $25.95 and $29.14. Similarly, we can claim with 95% confidence that the true population average wage for workers with only a high school diploma is somewhere between $13.12 and $16.31. Furthermore, the upper limit of the confidence interval ($16.31) for high school diploma is considerably lower than the lower limit for the confidence interval for a bachelor's degree ($25.95), meaning there is no overlap of the two confidence intervals. The fact that there is no overlap allows us to claim that the mean average wage for a bachelor's degree is probably higher than for workers with only a high school diploma. By contrast, when we compare the upper limit of the confidence interval for no high school with those with a high school diploma, the upper limit for no high school ($13.62) is higher than the lower limit for those with a high school diploma ($13.12). For example, the true population mean could be $13.50, which is included in both confidence intervals. As a result, we cannot claim that the population true average is higher for workers with a high school diploma versus no high school diploma. The real returns to education seem to be with a bachelor's degree. Frequency tables: . Bins have to be of equal size for a given frequency table. Otherwise the frequency table loses its meaning. They should be easy to read also. And I asked you to not create more than 10 bins. Please check the textbook's advice about creating bins for frequency tables. Here is one example of what you could have done for the bachelor's data: Wage Range Frequency Rel. Frequency 15t u c at is E .3 E u n: