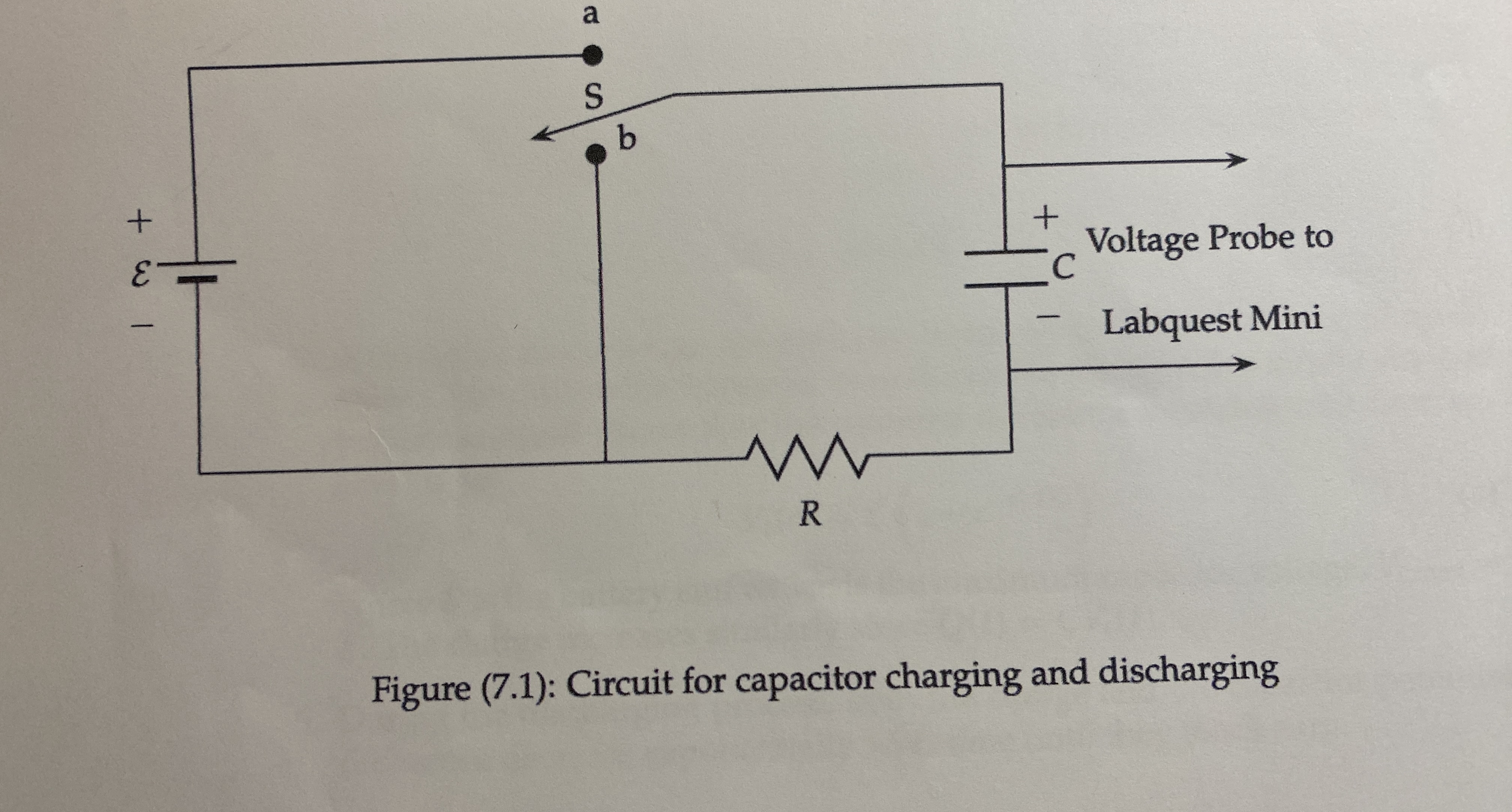
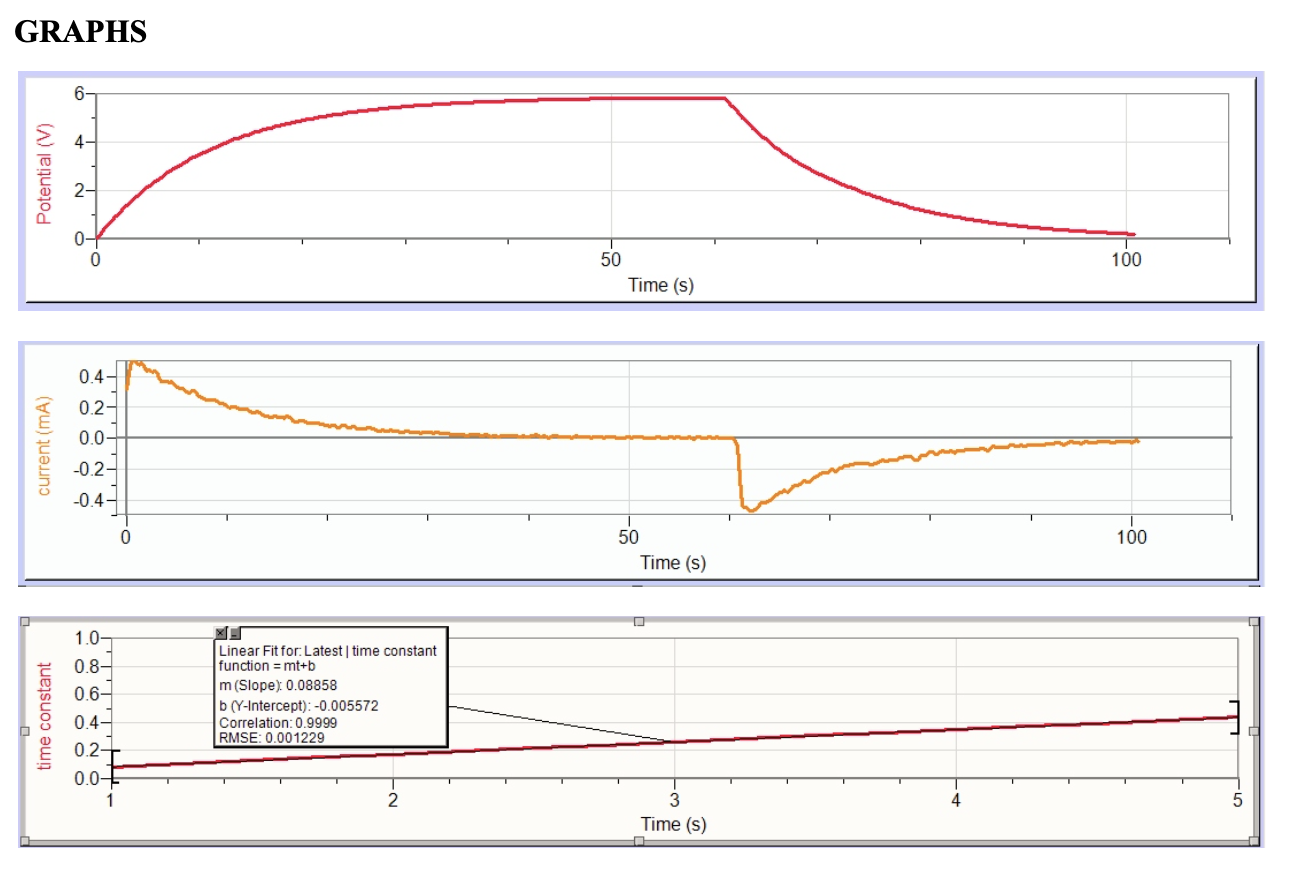
PHYS 2426 Engineering Physics II EXPERIMENT 7 CAPACITOR CHARGING AND DISCHARGING OBJECTIVE: The objective of this experiment is the study of capacitor charging and discharging by measuring the potential difference (voltage) across the capacitor as a function of time. From this measurement, the student will calculate the charge and the current as functions of time. The student will also calculate the time constant. THEORY: 1. A capacitor consists of two conducting objects (plates) separated by a non- conducting medium (dielectric). The capacitance of a capacitor is defined as the ratio of the charge on the one of the conductors to the potential difference between them, C = (1) 2. When a capacitor is connected to a power supply (such as a battery), it be- gins to charge up. During this process, both the charge, Q and the potential difference, Vc, are increasing and the electric current is decreasing. This will continue until both Q and Vc reach their maximum values and the electric current goes to zero indicating that the charging process has stopped. 3. The characteristic time which indicates how fast or slow a capacitor charges or discharges is called the time constant. It is the time it takes the potential difference (or the charge) to increase from zero to 0.632 (or 63.2%) of it's max- imum value. The time constant depends on the values of the capacitance and the resistance in the circuit and is given by T = RC (2) 4. A capacitor needs 5 time constants to charge up to 0.993 (or 99.3%) of maxi- mum value. When this happens, we will assume the capacitor is fully charged. Further analysis shows that the potential difference increases with time ac- cording to Vc (t ) = 8 (1 - e-+/RC ) (3) where & is the battery emf which is the maximum capacitor voltage, Vc,max = E. The charge increases similarly since Q(t) = CV.(t). 5. During the discharging process, both the charge and the capacitor potential difference decrease exponentially with time until they reach zero.APPARATUS: Capacitor about 2.0 mF (largest one on the capacitor board), resistor (decade box), power supply, DMM, capacitance meter, double throw switch and connecting wires. EXPERIMENTAL PROCEDURE: 1. Measure C and record its value. 2. Choose a value for R to give a time constant RC = 10.0 sec. This is the theo- retical value of the time constant, T. 3. Dial in this value of R and then use the DMM as an ohmmeter and adjust the value of as close as you can to the value you calculated in the last step. The Ohmmeter gives you a more accurate value. 4. Discharge the capacitor by connecting a wire across the leads for about a minute. 5. Wire the circuit as shown in the figure. 6. Clip the voltage probe to the capacitor observing the correct polarity and plug it in the Labquest Mini which plugs into the USB computer port. The data collected are the capacitor potential difference, V. as a function of time. 7. Open the folder "Capacitor charging and discharging" which should be on the desktop. 8. Click on the Collect button as you throw the switch to position "a". The ca- pacitor will start to charge and you will see the capacitor potential difference increase. Practice this timing process to ensure that the capacitor starts charg- ing at time t = 0.0. 9. When the time reaches 60.0 seconds ( 6 time constants), throw the switch to "b". The capacitor starts to discharge and the capacitor potential difference decreases to zero in the next 60.0 seconds. The potential difference Vc vs. time data are stored in a data table and will be used to calculate the charge, the current and the time constant. 10. Measure the emf ,&, of the power supply and record it in your data table. 11. From the collected data, we will calculate the charge, Q = CVc, the electric current I = de at and the time constant T. 12. Calculation of Charge. Follow the following steps: (a) Go to data on the main menu, drag down and click on new calculated column. (b) Give the new column a name (Charge), a short name (Q) and specify its units, milliCoulombs, mc. 2(c) In Expression, enter the numerical value of C (in mF) as a decimal num- ber and go to variables and choose "potential". Don't forget the multi- plication sign * (d) In the options tab, change the precision of the data to 6 decimal places. Click Done. (e) This will generate the electric charge data column. You do not need to graph the charge since it's graph looks exactly the same as the voltage. 13. Repeat step (12) to generate the electric current. (a) The electric current is the derivative of the electric charge. (b) The "derivative" operation is available for you to choose in the dialogue box. If you can not find it, get someone to help you. (c) Note that since Q is in units of mC, the current is in units of mA. (d) In the options tab, change the precision of the data to 6 decimal places. Click Done. (e) Go to the second graph on the screen, highlight the label on the vertical axis and change it to electric current which should be chosen from the "variables" list. (f) Change the scale on the vertical axis to a range appropriate for the cur- rent data. (g) Note that the current in the discharging phase flows in opposite direc- tion to the current in the charging phase. Since the charge is decreasing, the current will be negative. 14. The third new column contains the formula: f(t) = - In(1.0 - "potential" / E) (4) (a) Get the natural log function In from the functions available in the dia- logue box. (b) Get "potential" from the variables list and enter the numerical value for E. (c) This will give a straight line graph (for the first several seconds) whose slope is the reciprocal of the time constant. Graph this function for the first 5 seconds only. (d) Calculate the slope of the straight line and from this slope calculate the time constant.a S b + + C Voltage Probe to 1 Labquest Mini R Figure (7.1): Circuit for capacitor charging and dischargingGRAPHS Potential (V) N 50 100 Time (s) 0.4- 0.2- 0.0- current (mA) -0.2- -0.4- 50 100 Time (s) 1.0- Linear Fit for: Latest | time constant 0.8- function = mt+b 0.6- m (Slope): 0.08858 b (Y-Intercept): -0.005572 time constant 0.4- Correlation: 0.9999 RMSE: 0.001229 0.2- 0.0-7 3 Time (s)