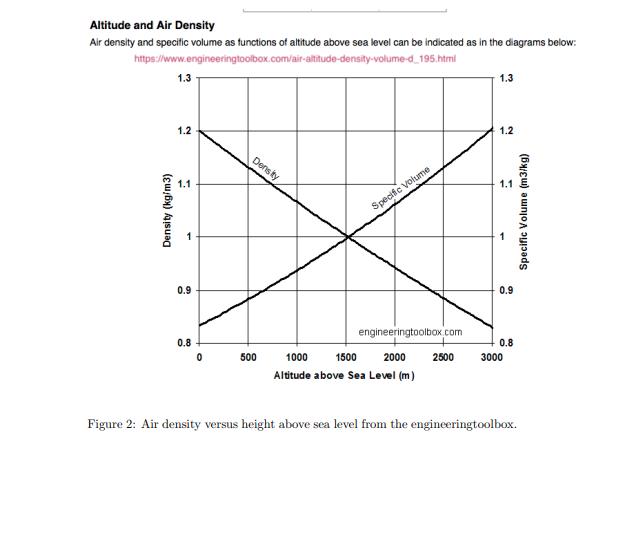
PHYS5301, Aerodynamic Drag Forces In introductory mechanics we study projectile motion in an airless environment. The only forces we assume are from gravity. In this exercise we will study projectile motion in a realistic environment. The equations of motion depend on physical parameters that are determined empirically. The information needed is readily available online using NASA and engineering web sites. The exercise will ignore the change of gravitational acceleration for motion near the surface of the earth. The forces exerted on a mass, m. are W, the weight and the drag force . F = +W + W a= m In equation la the total force is, F. We want to determine the acceleration, a. Knowing the acceleration we follow the trajectory of m in steps of time, dt. This must be done numerically. Consider the displacement, r(t), and velocity, (t), at any given moment of time, t. du= adt (t + dt) = (t) + du dr = u(t)dt r(t + dt) r(t) + dr (la) (1b) (B) The drag equation (see for example a NASA website) is Ca(v)pv A 2 You can employ the steps in equations 2a-2d in a computer code you write or use one of the mathematical packages available. By selecting a step size, dt you are deriving an analytical solution (by quadrature) according to the discus- sion in Finn's book, see equation 1.90, for example. You keep track of the total time. The physics is straightforward. In any given problem the issue is not so much a mathematical procedure but be aware of the physical condition of the particle at each step, dt. Equation 1.90 is for a simple case where the physical conditions of the particle are not time dependent. Following a 45 caliber bullet. Use MKS units! (A) A 45 caliber bullet has a mass of 13g and a cross sectional area of A = 1.06 x 10-4m. Assume the muzzle velocity is v= 275m/s. For this cal- culation ignore drag. What is the maximum height, in meters, and the time of flight to maximum height in seconds? At what time after firing does the bullet return to ground? Assume the initial velocity is vertical. D= (2a) (2b) (2c) (2d) (3) In equation 3 the coefficent of drag for this type of bullet depnds on the speed, u, through the air see figure 1, Ca(v) and on air density, p is the air den- sity. The direction of the drag force is opposite the velocity of the bullet. Note that if p = 0) we are back in the introductory physics situation. When you solve the problem, using whatever algorithm you chose, check, as a matter of princi- ple, that if p= 0 your algorithm gives you the answer in (A). Also, as a matter of practice, try a few steps dt to see if your answers agree within some criteria you choose for reliability of the procedure. In order to apply equation 3 you should consider the importance of the dependence of the air density, p(h), on al- titude, h, here's an example from figure 2 and on the local speed, u from figure 1. (Question1) What is the maximum height the bullet reaches and the time to maximum height if it starts from sea level? (Question2) What is the time it takes for the bullet to fall back to the ground and its speed? (Question3) Suppose the bullet is fired from Colorado Springs(altitude 1840m). What is the maximum height of the bullet and the time to maximum height? (Question4) What is the time it takes for the bullet to fall back to the ground and its speed in Colorado Springs? (Question5) What is the terminal velocity of the bullet? 18 values for G1 bullet v/mach1 drag coefficient 0. 0.266 0.244 0.242 0.222 0.218 0.21 0.11046 0.13676 0.28404 0.3156 0.37346 0.49444 0.61016 0.6838 0.70484 0.73114 0.7627 0.79952 0.8153 0.85738 0.8942 0.91524 0.95732 0.204 0.202 0.212 0.216 0.226 0.232 0.25 0.26 0.294 0.33 0.366 0.402 U Figure 1: Drag coefficient for a G1 bullet in air as a function of speed, v, mach where mach1 = 343m/s. - Altitude and Air Density Air density and specific volume as functions of altitude above sea level can be indicated as in the diagrams below: https://www.engineeringtoolbox.com/air-altitude-density-volume-d_195.html Density (kg/m3) 1.3 1.2 1.1 0.9 0.8 0 Density 500 Specific Volume engineeringtoolbox.com 1000 1500 2000 2500 Altitude above Sea Level (m) 1.3 1.2 1.1 0.9 0.8 3000 Specific Volume (m3/kg) Figure 2: Air density versus height above sea level from the engineeringtoolbox.