please also try to show me your work so i can understand it

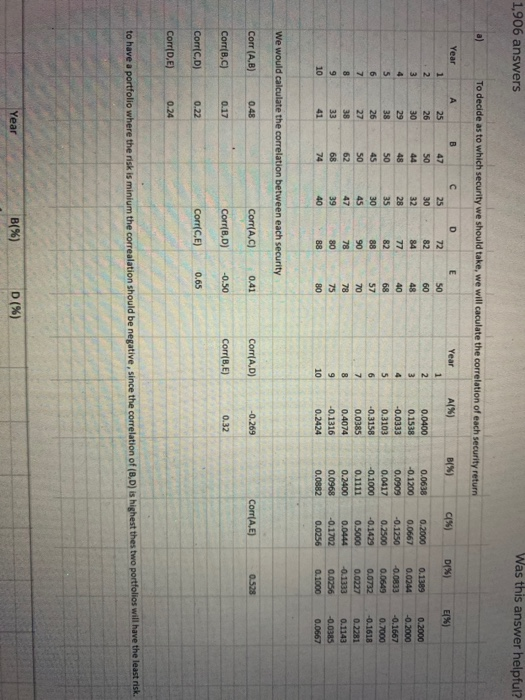
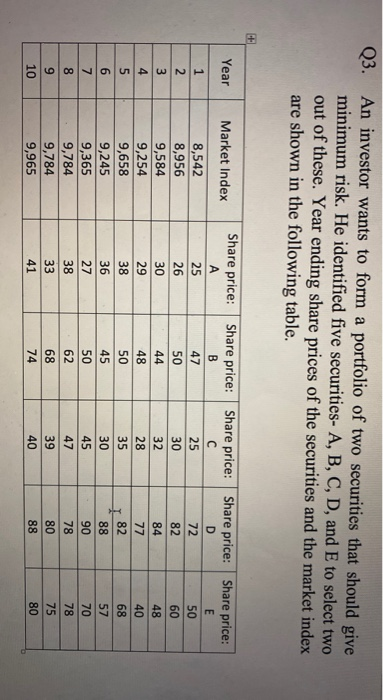
U U TION. Suggest the proportion of investment in each security so that the portfolio has the minimum risk. Q3. An investor wants to form a portfolio of two securities that should give minimum risk. He identified five securities- A, B, C, D, and E to select two out of these. Year ending share prices of the securities and the market index are shown in the following table. Year Market Index Share price: Share price: Share price: Share price: Share price: 25 47 25 50 30 60 BLOWN 8,542 8,956 9,584 9,254 9,658 9,245 9,365 9,784 9,784 9,965 80 1,906 answers Was this answer helpful? To decide as to which security we should take, we will caculate the correlation of each security return Year Tear A%) B1%) 01%) D1%) E%) 0.0400 0.1538 -0.0333 0.3103 -0.3158 0.0385 0.4074 -0.1316 .2424 0.0638 -0.1200 0.0909 0.0417 -0.1000 0.1111 0.2400 0.0968 0.0882 0.2000 0.0667 -0.1250 0.2500 -0.1429 0.5000 0.0444 -0.1702 0.0256 0.1389 0.0244 0.0833 0.0649 0.0732 0.0227 0.1333 0.0256 0.1000 0.2000 -0.2000 -0.1667 0.7000 -0.1618 0.2281 0.1143 -0.0385 0.0667 100 We would calculate the correlation between each security Corr(A,B) 0.48 Corr(A,C) 0.41 Corr(A,D) -0.269 Corr(A.E) 0528 Corr(B,C) 0.17 Corr(BD) -0.50 Corr(BE) 0.32 Corr(CD) 0.22 Corr(CE) 0.65 Corr(D,E) 0.24 to have a portfolio where the risk is minium the correalation should be negative, since the correlation of (BD) is highest thes two portfolios will have the least risk. Year B (%) (%) B(%) (%) 0.0638 -0.1200 0.0909 0.0417 -0.1000 0.1111 0.2400 0.0968 0.0882 0.1389 0.0244 -0.0833 0.0649 0.0732 0.0227 -0.1333 0.0256 0.1000 Mean return 0.0569 0.0259 Standard deviation 0.1098 We will be using the minimum variance formula to calculate the weights of the lest varinace Weight of B (0.0861^2-(-0.5*0.1098*0.0861))/(0.1098^2 +0.0861^2-2'(-0.5)*0.1098*0.0861) 0.4197 Weight of D= (1-0.4197) 0.5803 Standard deviation of the portfolio (0.4197^2 *0.1098^2 +0.5803^2 *0,0861^2+20.4197*0.5803"0.1098*0.0861"(-0.5))^(1/2) 0.0481 so the risk of the portfolio is 4.815 Expected return from the portfolio (0.0569"0.41970.5803*0,0259) The weight of B would be and of D would be 41.97% 5803