Solve the incompressible boundary layer equations for laminarflow over a flat plate, assuming that viscous dissipation isactive. The boundary layer equations

are given below:

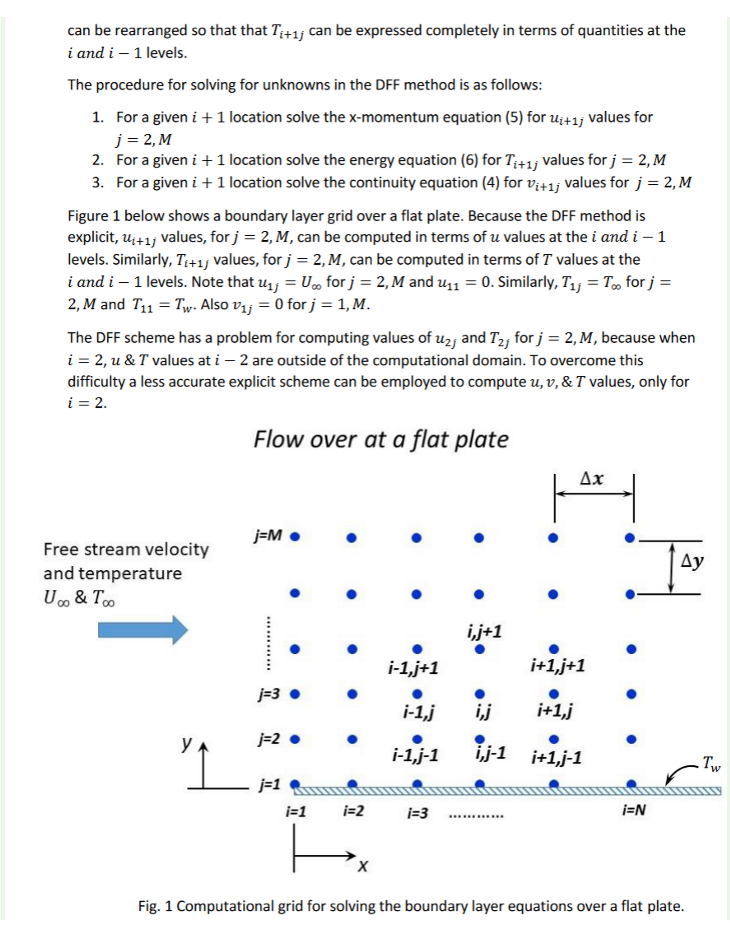
Continuity equation: x-momentum equation: Energy equation: U T T x +v v + x y du ????u +v x = =0 aT eq. (1) u = (5) 3,72424 eq. (2) Jy + ( 7 ) (34) eq. (3) The boundary conditions for equations (1), (2), and (3) are given below: At x = 0: u(0, y) = U, v(0,y) = 0, T(0, y) = Too At y = 0: u(x,0) = 0, v(x,0) = 0, T(x,0) = Tw At y o: u(x, 0) = U, v(x,) = 0, T(x, 0) = To You are being assigned to analyze the boundary layer for flow over a flat plate. Laminar flow of oil over a flat plate. U = 10 m, T = 37C, Tw= 17C (wall temperature) sec The energy equation (3) has a term for viscous dissipation. Properties of the oil are given in the table below (evaluated at 27 C). These properties may be assumed to be constant throughout the computational domain. Density Specific heat Dynamic viscosity 884 kg/m 1.91 kJ/kg-K 0.486 N-sec/m Thermal conductivity 0.145 W/m-K Prandtl No. 6400 The boundary layer (BL) equations are parabolic in the x (stream wise) coordinate. What this means is that the dependent variables at a given x location do not depend on downstream values, i.e. they only depend on upstream values. It turns out that this simplifies the solution process as will be discussed below.