please answer 3-6 need to calculation process

3.The fair value of bond B2 is closest to:

A. 1,069.34. B. 1,111.51. C. 1,153.68.

4. The market price of bond B2 is 1,090. If the bond is purchased at this price and there is a default on Date 3, the rate of return to the bond buyer would be closest to: A. 28.38%. B. 41.72%.

   C. 69.49%.

5. Bond B3 will have a modified duration of 2.75 at the end of the year. Based on the rep-

   resentative one-year corporate transition matrix in Exhibit 7 of the reading and assuming no default, how should the analyst adjust the bonds yield to maturity (YTM) to assess the expected return on the bond over the next year?

   1. Add 7.7 bps to YTM.

   2. Subtract 7.7 bps from YTM.

   3. Subtract 9.0 bps from YTM.

6. David Lok has estimated the probability of default of bond B1 to be 1.50%. He is pre-

   senting the approach the research team used to estimate the probability of default. Which of the following statements is Lok likely to make in his presentation if the team used a reduced-form credit model?

   1. Option pricing methodologies were used, with the volatility of the underlying asset

      estimated based on historical data on the firms stock price.

   2. Regression analysis was used, with the independent variables including both firm-

      specific variables, such as the debt ratio and return on assets, and macroeconomic

      variables, such as the rate of inflation and the unemployment rate.

   3. The default barrier was first estimated followed by the estimation of the probability of default as the portion of the probability distribution that lies below the default barrier.

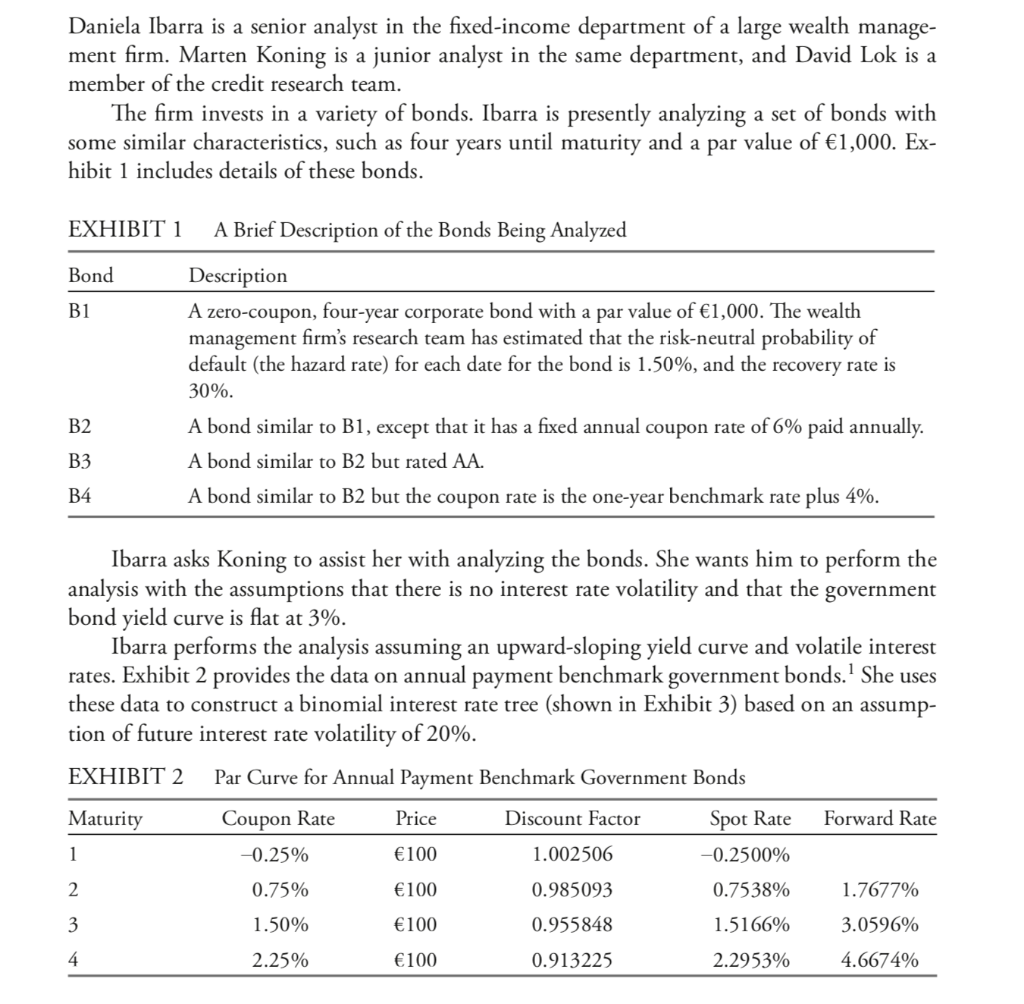
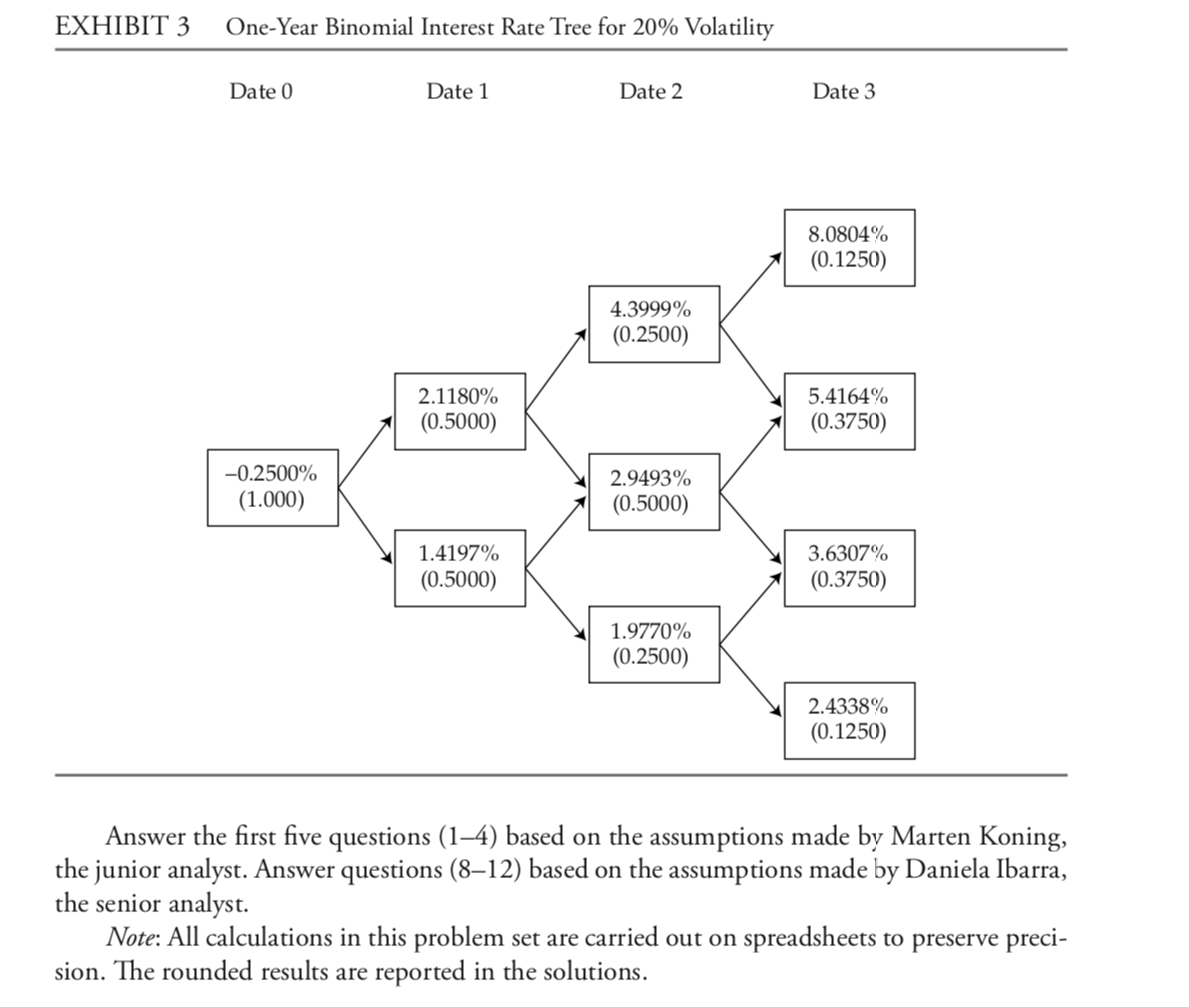
Daniela Ibarra is a senior analyst in the fixed-income department of a large wealth manage- ment firm. Marten Koning is a junior analyst in the same department, and David Lok is a member of the credit research team. The firm invests in a variety of bonds. Ibarra is presently analyzing a set of bonds with some similar characteristics, such as four years until maturity and a par value of 1,000. Ex- hibit 1 includes details of these bonds. EXHIBIT 1 A Brief Description of the Bonds Being Analyzed Bond B1 Description A zero-coupon, four-year corporate bond with a par value of 1,000. The wealth management firm's research team has estimated that the risk-neutral probability of default (the hazard rate) for each date for the bond is 1.50%, and the recovery rate is 30%. A bond similar to B1, except that it has a fixed annual coupon rate of 6% paid annually. A bond similar to B2 but rated AA. A bond similar to B2 but the coupon rate is the one-year benchmark rate plus 4%. B2 B3 B4 Ibarra asks Koning to assist her with analyzing the bonds. She wants him to perform the analysis with the assumptions that there is no interest rate volatility and that the government bond yield curve is flat at 3%. Ibarra performs the analysis assuming an upward-sloping yield curve and volatile interest rates. Exhibit 2 provides the data on annual payment benchmark government bonds. She uses these data to construct a binomial interest rate tree (shown in Exhibit 3) based on an assump- tion of future interest rate volatility of 20%. EXHIBIT 2 Par Curve for Annual Payment Benchmark Government Bonds Maturity Coupon Rate Discount Factor Forward Rate -0.25% 1.002506 -0.2500% Price Spot Rate 1 100 2 0.75% 100 0.985093 0.7538% 1.7677% 3 1.50% 100 0.955848 1.5166% 3.0596% 4 2.25% 100 0.913225 2.2953% 4.6674% EXHIBIT 3 One-Year Binomial Interest Rate Tree for 20% Volatility Date 0 Date 1 Date 2 Date 3 8.0804% (0.1250) 4.3999% (0.2500) 2.1180% (0.5000) 5.4164% (0.3750) -0.2500% (1.000) 2.9493% (0.5000) 1.4197% (0.5000) 3.6307% (0.3750) 1.9770% (0.2500) 2.4338% (0.1250) Answer the first five questions (14) based on the assumptions made by Marten Koning, the junior analyst. Answer questions (812) based on the assumptions made by Daniela Ibarra, the senior analyst. Note: All calculations in this problem set are carried out on spreadsheets to preserve preci- sion. The rounded results are reported in the solutions. Daniela Ibarra is a senior analyst in the fixed-income department of a large wealth manage- ment firm. Marten Koning is a junior analyst in the same department, and David Lok is a member of the credit research team. The firm invests in a variety of bonds. Ibarra is presently analyzing a set of bonds with some similar characteristics, such as four years until maturity and a par value of 1,000. Ex- hibit 1 includes details of these bonds. EXHIBIT 1 A Brief Description of the Bonds Being Analyzed Bond B1 Description A zero-coupon, four-year corporate bond with a par value of 1,000. The wealth management firm's research team has estimated that the risk-neutral probability of default (the hazard rate) for each date for the bond is 1.50%, and the recovery rate is 30%. A bond similar to B1, except that it has a fixed annual coupon rate of 6% paid annually. A bond similar to B2 but rated AA. A bond similar to B2 but the coupon rate is the one-year benchmark rate plus 4%. B2 B3 B4 Ibarra asks Koning to assist her with analyzing the bonds. She wants him to perform the analysis with the assumptions that there is no interest rate volatility and that the government bond yield curve is flat at 3%. Ibarra performs the analysis assuming an upward-sloping yield curve and volatile interest rates. Exhibit 2 provides the data on annual payment benchmark government bonds. She uses these data to construct a binomial interest rate tree (shown in Exhibit 3) based on an assump- tion of future interest rate volatility of 20%. EXHIBIT 2 Par Curve for Annual Payment Benchmark Government Bonds Maturity Coupon Rate Discount Factor Forward Rate -0.25% 1.002506 -0.2500% Price Spot Rate 1 100 2 0.75% 100 0.985093 0.7538% 1.7677% 3 1.50% 100 0.955848 1.5166% 3.0596% 4 2.25% 100 0.913225 2.2953% 4.6674% EXHIBIT 3 One-Year Binomial Interest Rate Tree for 20% Volatility Date 0 Date 1 Date 2 Date 3 8.0804% (0.1250) 4.3999% (0.2500) 2.1180% (0.5000) 5.4164% (0.3750) -0.2500% (1.000) 2.9493% (0.5000) 1.4197% (0.5000) 3.6307% (0.3750) 1.9770% (0.2500) 2.4338% (0.1250) Answer the first five questions (14) based on the assumptions made by Marten Koning, the junior analyst. Answer questions (812) based on the assumptions made by Daniela Ibarra, the senior analyst. Note: All calculations in this problem set are carried out on spreadsheets to preserve preci- sion. The rounded results are reported in the solutions