Question
Please answer ALL parts! This is for a course in Probability Theory. 42) Computational Problem. Here is a probabilistic method for computing the area of
 Please answer ALL parts! This is for a course in Probability Theory.
Please answer ALL parts! This is for a course in Probability Theory.
42) Computational Problem. Here is a probabilistic method for computing the area of a given subset S of the unit square. The method uses a sequence of independent random selections of points in the unit square [0,1] x [0,1], according to a uniform probability law. if the ith point belongs to the subset S the value of a random variable Xi is set to 1, and otherwise it is set to 0. let x1, x2, ... be the sequence of random variables thus defined, and for any n, let
Sn = 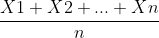 .
.
a) Show that E[Sn] is equal to the area of the subset S, and that var(Sn) diminishes to 0 as n increases.
b) Show that to calculate Sn, it is sufficient to know Sn-1 and Xn, so the past values of Xk, k=1, ... , n-1, do not need to be remembered. Give a formula.
c) Write a computer program to generate Sn for n = 1, 2, ..., 10000, using the computer's random number generator, for the case where the subset S is the circle inscribed within the unit square. How can you use your program to measure experimentally the value of 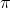 ?
?
d) Use a similar computer program to calculate approximately the area of the set of all (x,y) that lie within the unit square and satisfy 0  cos
cos x + sin
x + sin y
y  1.
1.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


