please answer all the questions.
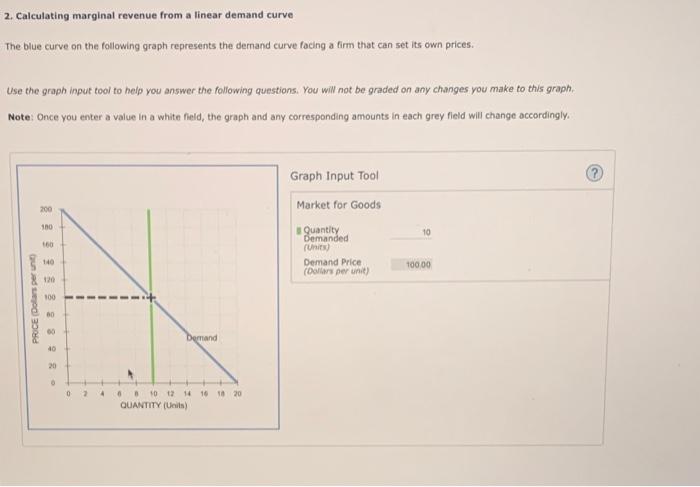
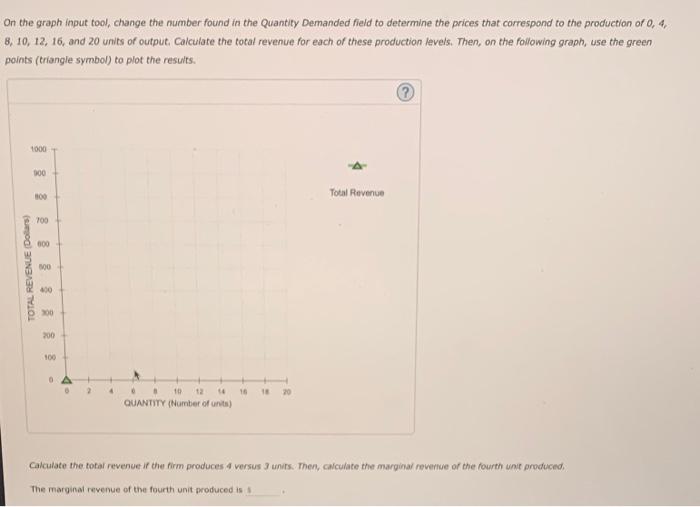
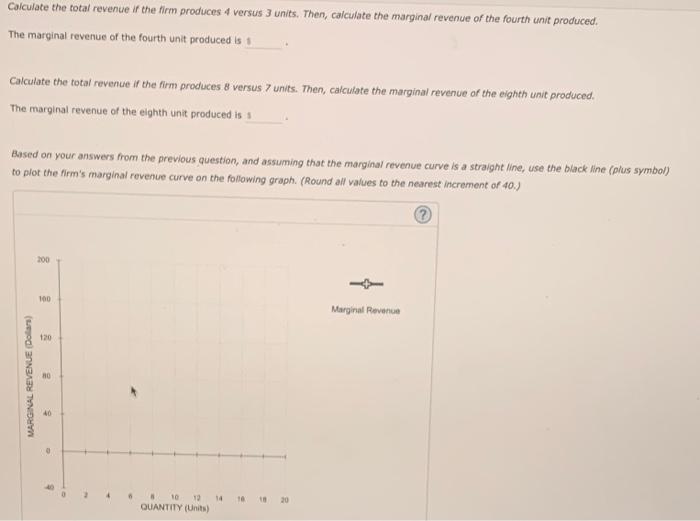
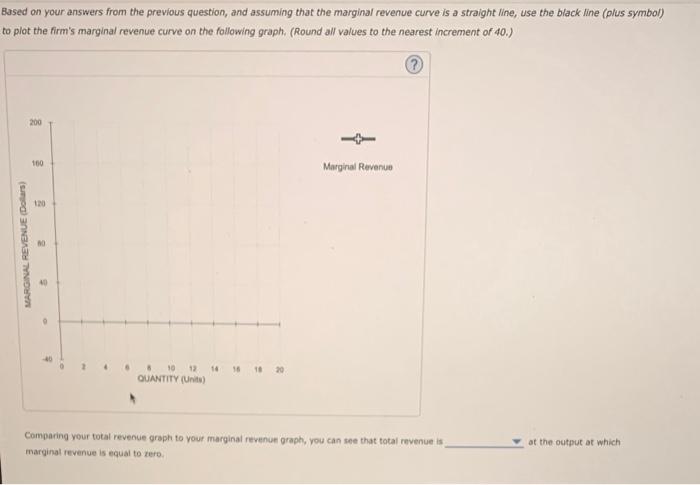
2. Calculating marginal revenue from a linear demand curve The blue curve on the following graph represents the dernand curve facing a firm that can set its own prices. Use the graph input tool to help you answer the following questions. You will not be graded on any changes you make to this graph. Note: Once you enter a value in a white field, the graph and any corresponding amounts in each grey fleld will change occordingly. Graph Input Tool On the graph input tool, change the number found in the Quantity Demanded field to determine the prices that correspond to the production of 0 , 4 , 8, 10, 12, 16, and 20 units of output. Calculate the total revenue for each of these production levels. Then, on the following graph, use the green points (triangle symbol) to plot the results. Calculate the total revenue if the firm produces 4 versus 3 unirs. Then, calculate the marginal revernue of the fourth unit produced. The marginal revenue of the fourth unit produced is Calculate the total revenue if the firm produces 4 versus 3 units. Then, calculate the marginal revenue of the fourth unit produced. The marginal revenue of the fourth unit produced is is Calculate the total revenue if the firm produces 8 versus 7 units. Then, calculate the marginal revenue of the eighth unit produced. The marginal revenue of the eighth unit produced is 1 Based on your answers from the previous question, and assuming that the marginal revenue curve is a straight line, use the black line (plus symbol to plot the firm's marginal revenue curve on the following graph. (Round all values to the nearest increment of 40 .) Jased on your answers from the previous question, and assuming that the marginal revenue curve is a straight line, use the black line (plus symbol) o plot the firm's marginal revenue curve on the following graph. (Round all values to the nearest increment of 40 .) Comparing your total revenue graph to your marginal revenue graph, you can see that total revenue is of the output at which marginal tevenue is equal to zere. 2. Calculating marginal revenue from a linear demand curve The blue curve on the following graph represents the dernand curve facing a firm that can set its own prices. Use the graph input tool to help you answer the following questions. You will not be graded on any changes you make to this graph. Note: Once you enter a value in a white field, the graph and any corresponding amounts in each grey fleld will change occordingly. Graph Input Tool On the graph input tool, change the number found in the Quantity Demanded field to determine the prices that correspond to the production of 0 , 4 , 8, 10, 12, 16, and 20 units of output. Calculate the total revenue for each of these production levels. Then, on the following graph, use the green points (triangle symbol) to plot the results. Calculate the total revenue if the firm produces 4 versus 3 unirs. Then, calculate the marginal revernue of the fourth unit produced. The marginal revenue of the fourth unit produced is Calculate the total revenue if the firm produces 4 versus 3 units. Then, calculate the marginal revenue of the fourth unit produced. The marginal revenue of the fourth unit produced is is Calculate the total revenue if the firm produces 8 versus 7 units. Then, calculate the marginal revenue of the eighth unit produced. The marginal revenue of the eighth unit produced is 1 Based on your answers from the previous question, and assuming that the marginal revenue curve is a straight line, use the black line (plus symbol to plot the firm's marginal revenue curve on the following graph. (Round all values to the nearest increment of 40 .) Jased on your answers from the previous question, and assuming that the marginal revenue curve is a straight line, use the black line (plus symbol) o plot the firm's marginal revenue curve on the following graph. (Round all values to the nearest increment of 40 .) Comparing your total revenue graph to your marginal revenue graph, you can see that total revenue is of the output at which marginal tevenue is equal to zere