Please answer all the required questions in detail I hope the answer is not copy-paste I hope that the answer will be according to the concepts in the chapter 3

The following article summarizes the findings of a study by economist Joel Waldfogel on the deadweight loss of gift-giving:

https://www.aeaweb.org/research/did-holiday-gift-giving-just-create-loss

Read the article and t answering the following questions: 1- Briefly explain the findings of Waldfogel's paper on the deadweight loss of gift-giving. 2- Some studies disagree with Waldfogel findings. What factors may increase the value of the gift relative to its purchased value? 3- Try to explain Waldfogel's findings using the concepts we've studied in Chapter 3 (Most bonus points will be based on your answer to this question).

chapter 3

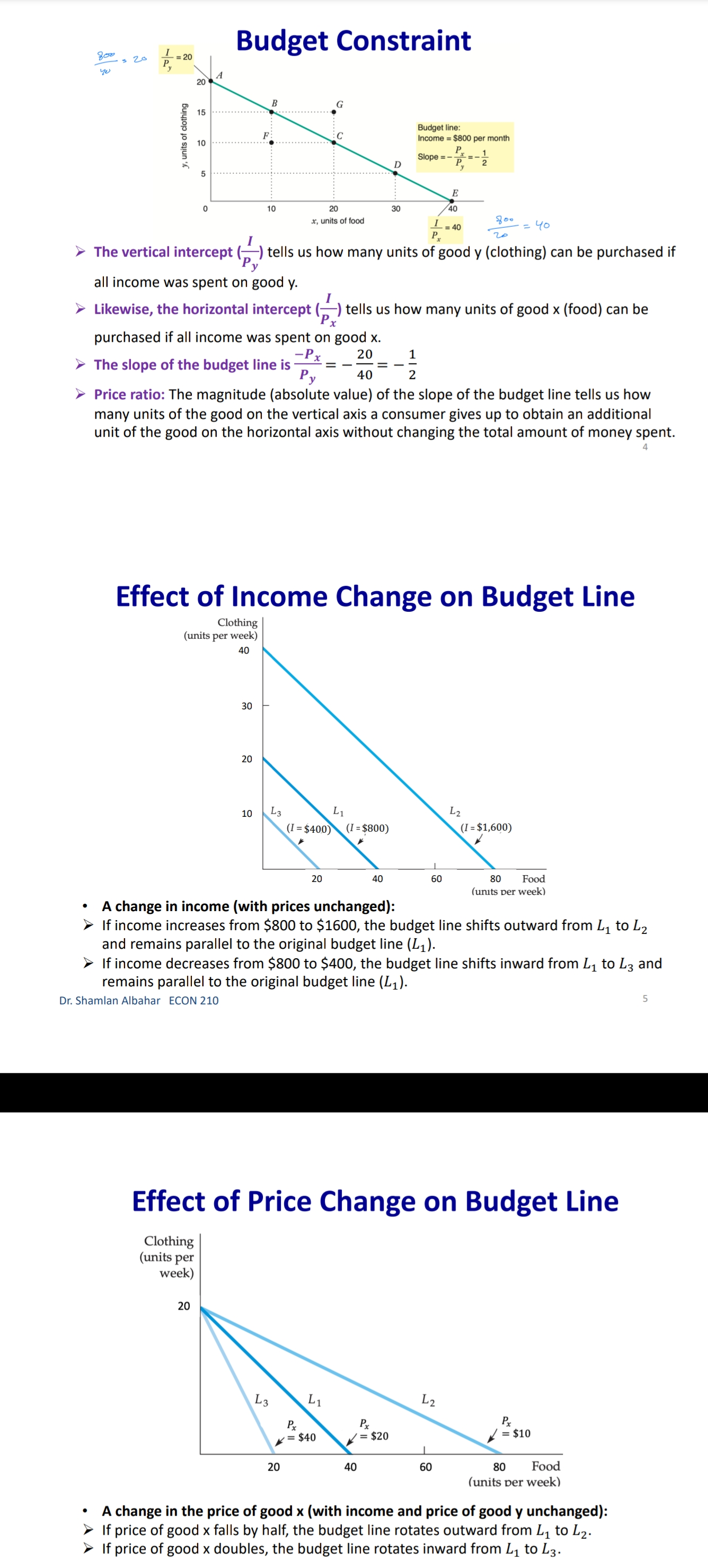
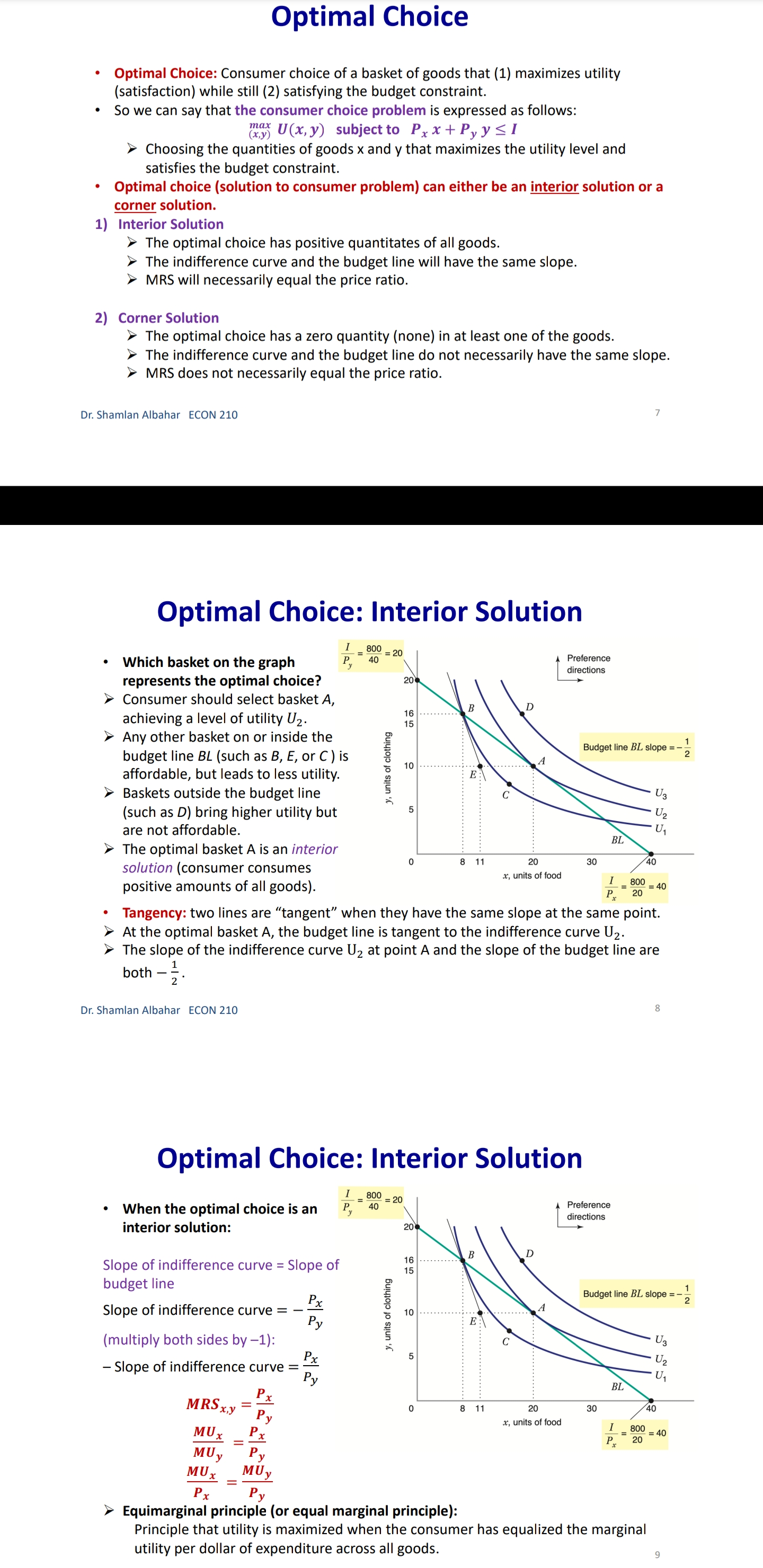
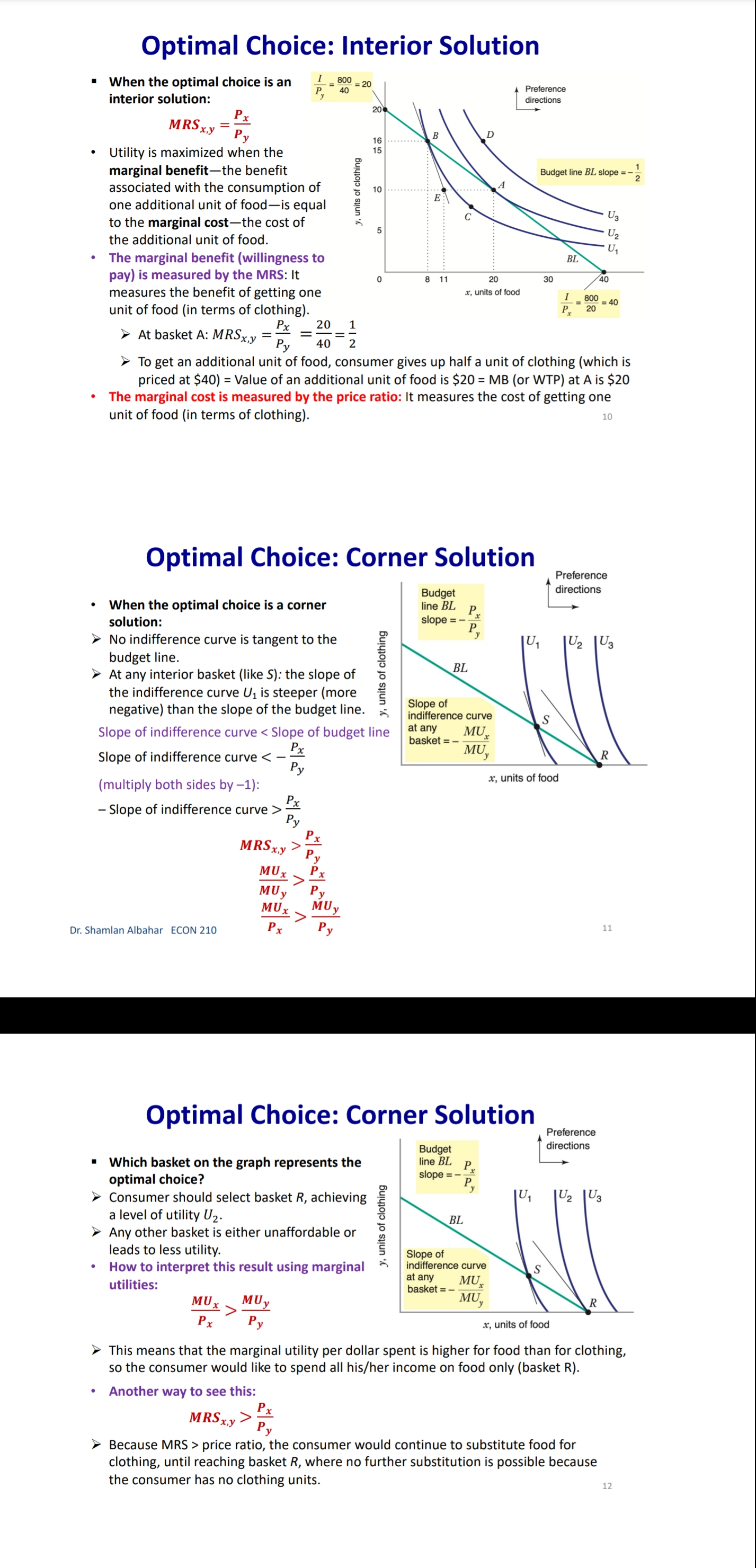
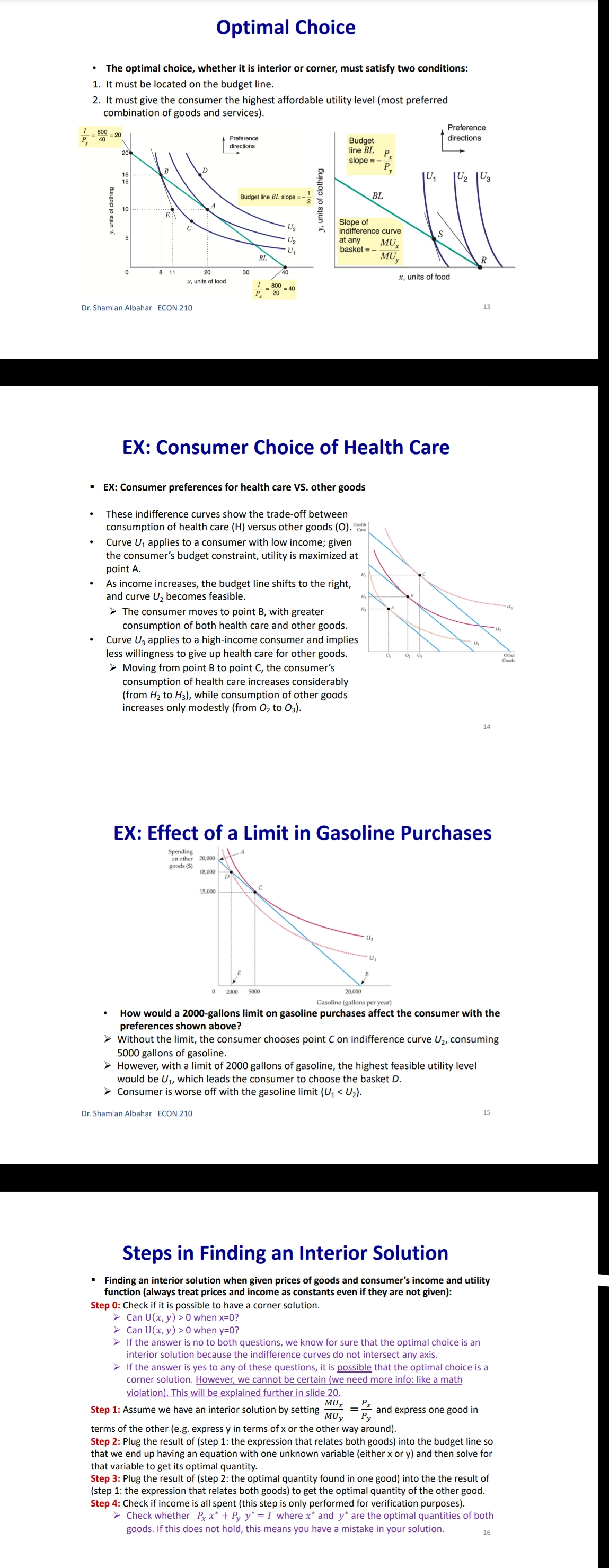
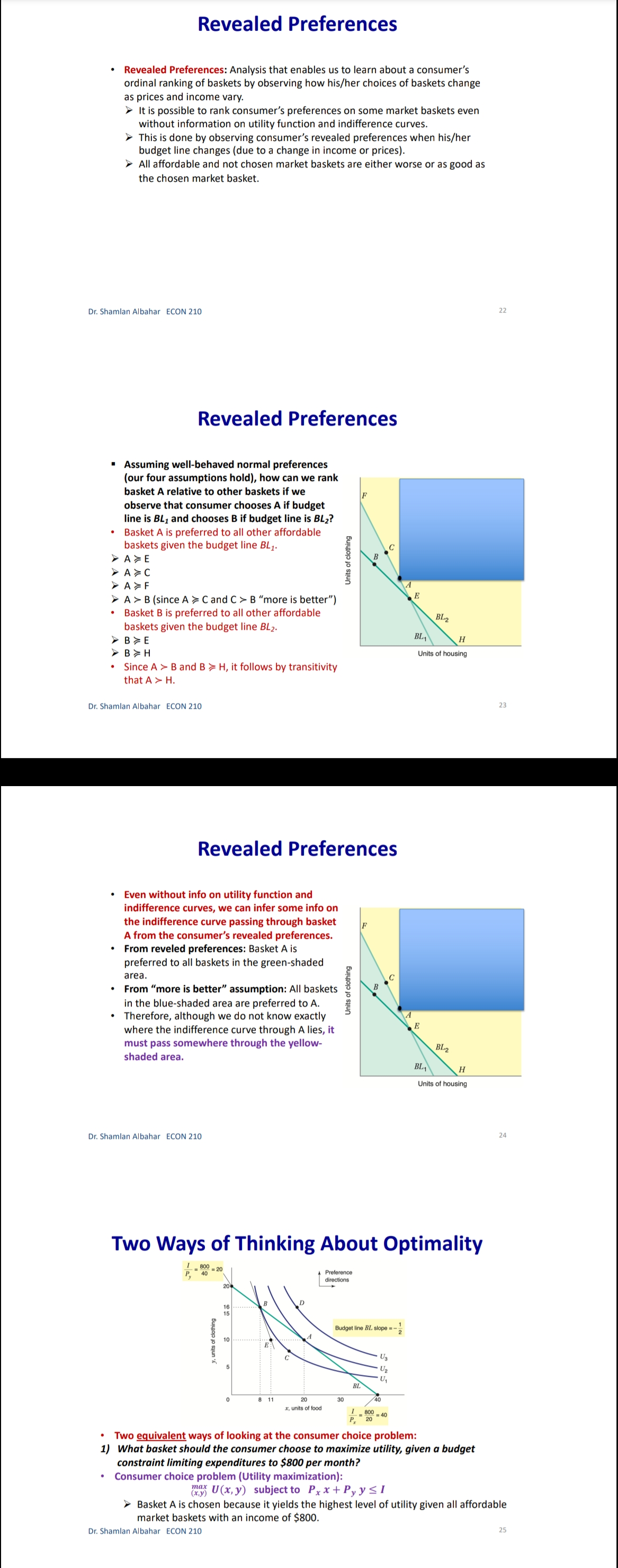
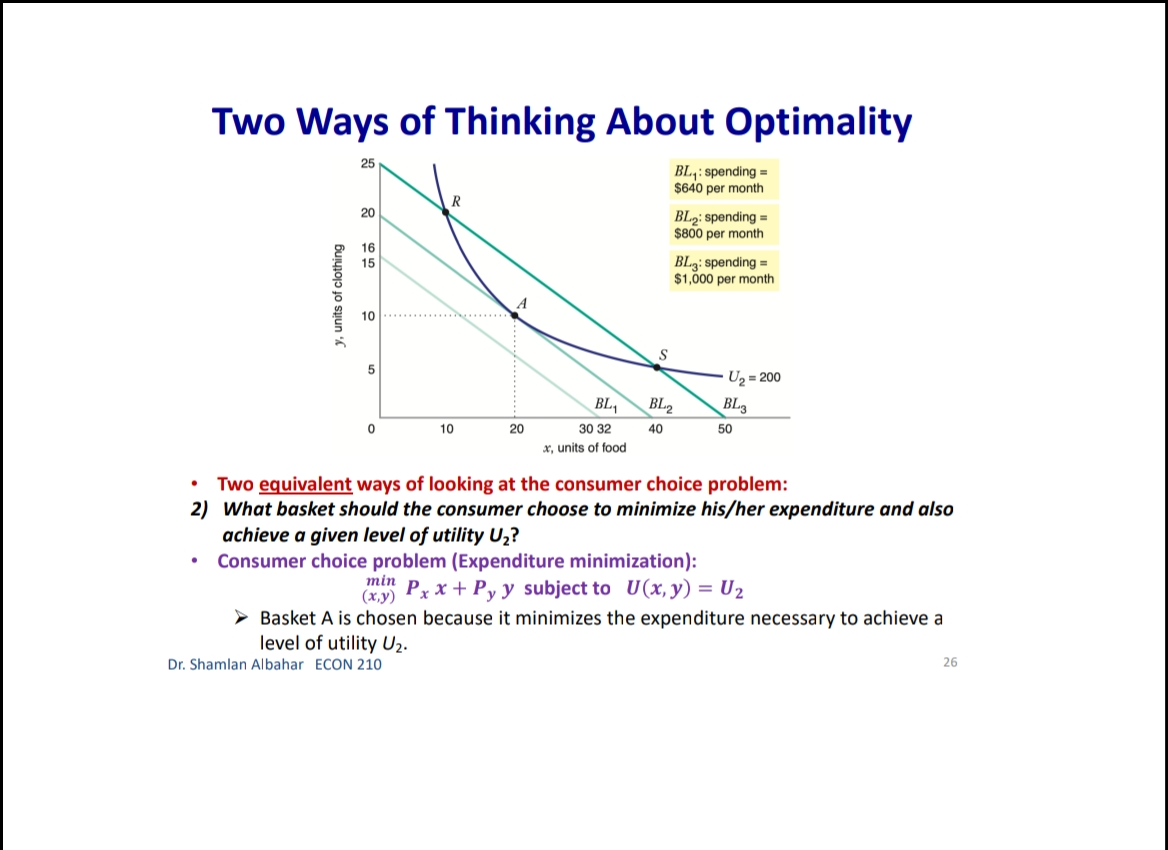
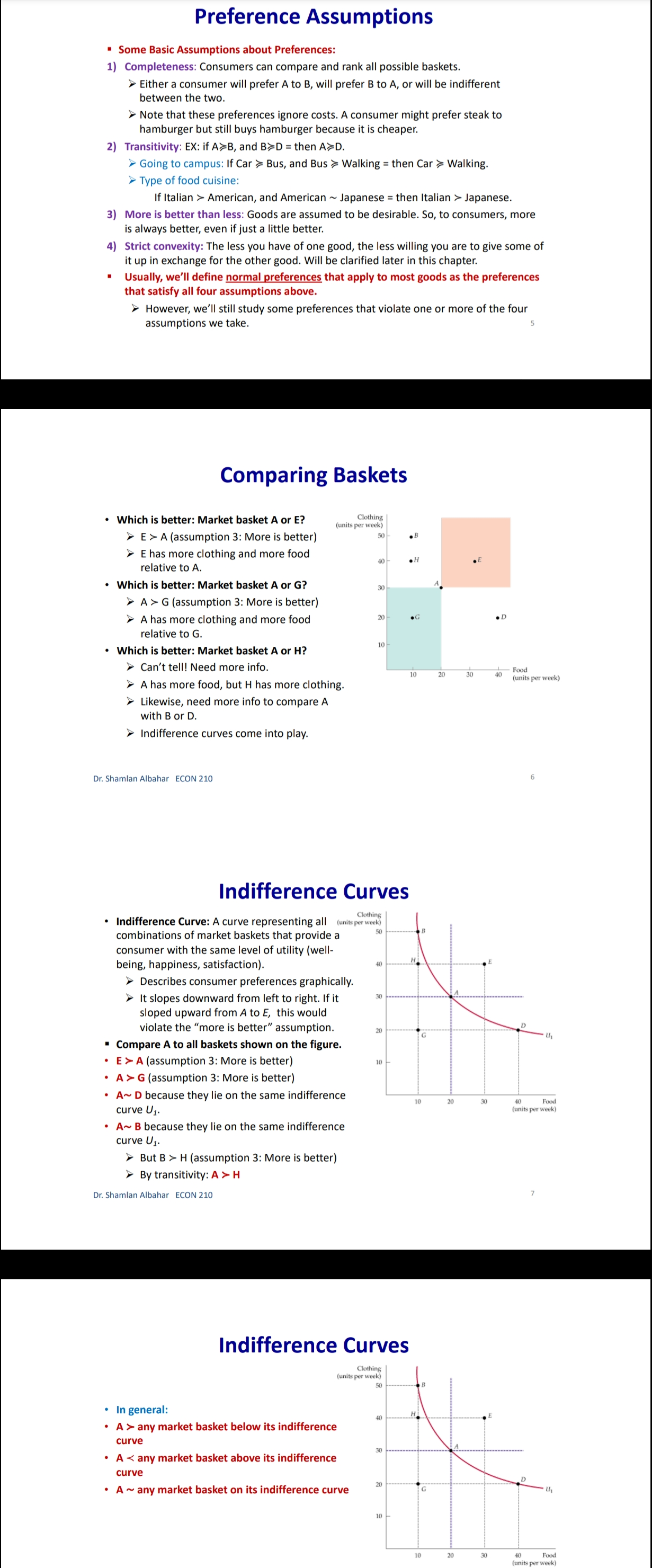
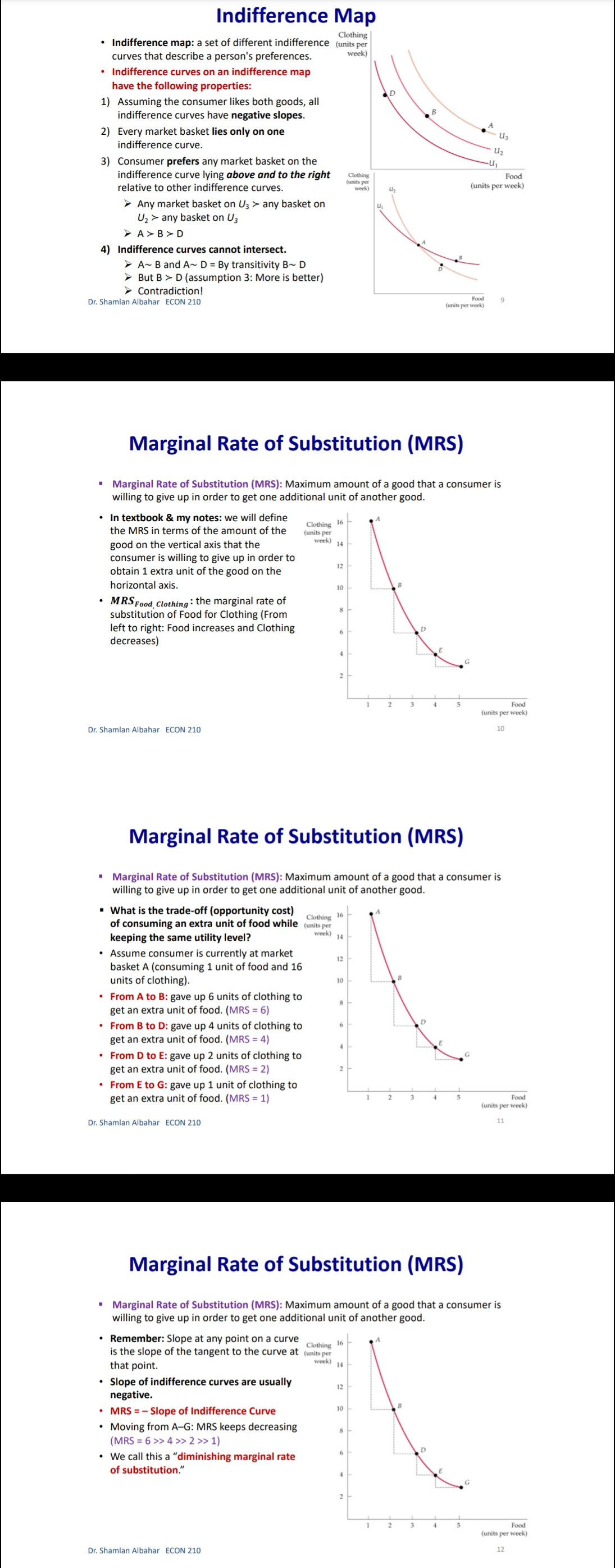
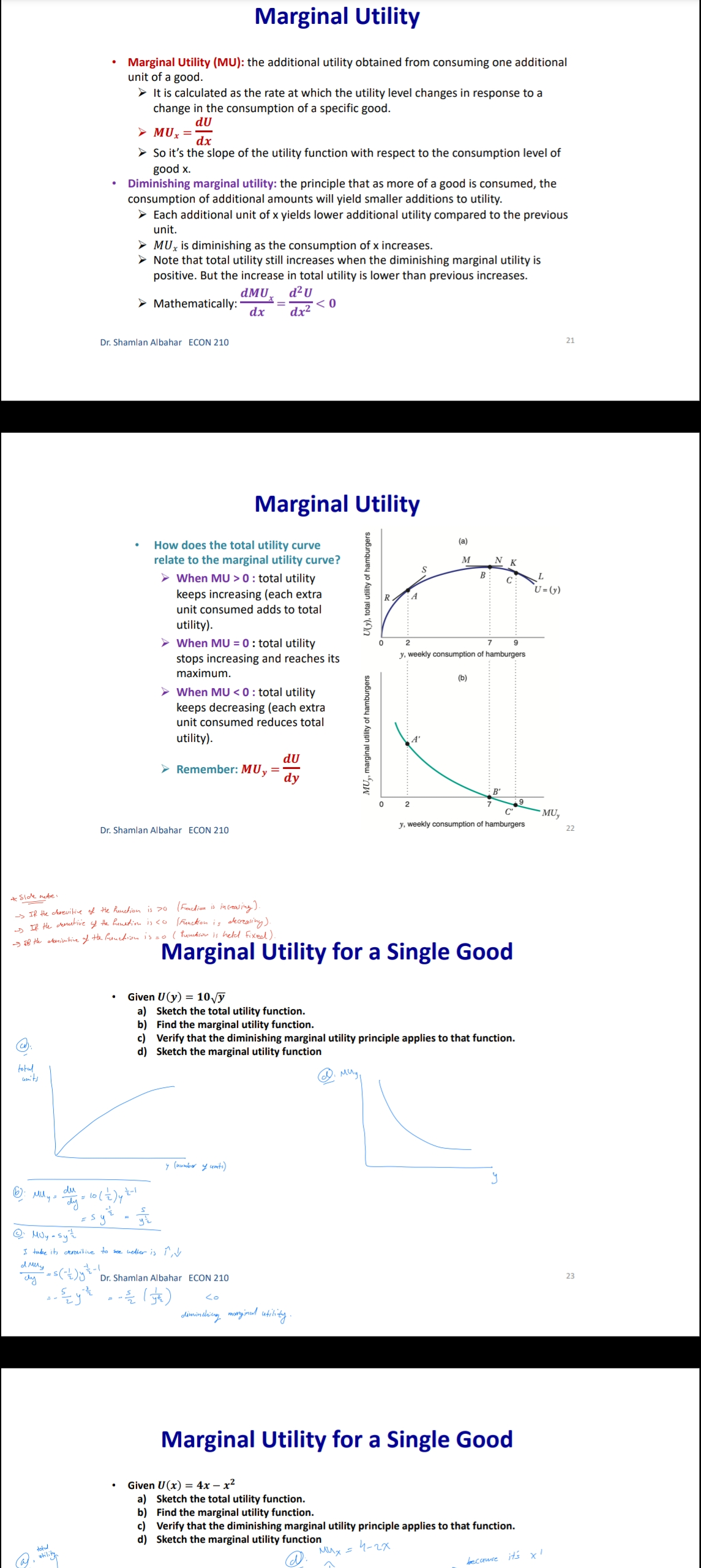
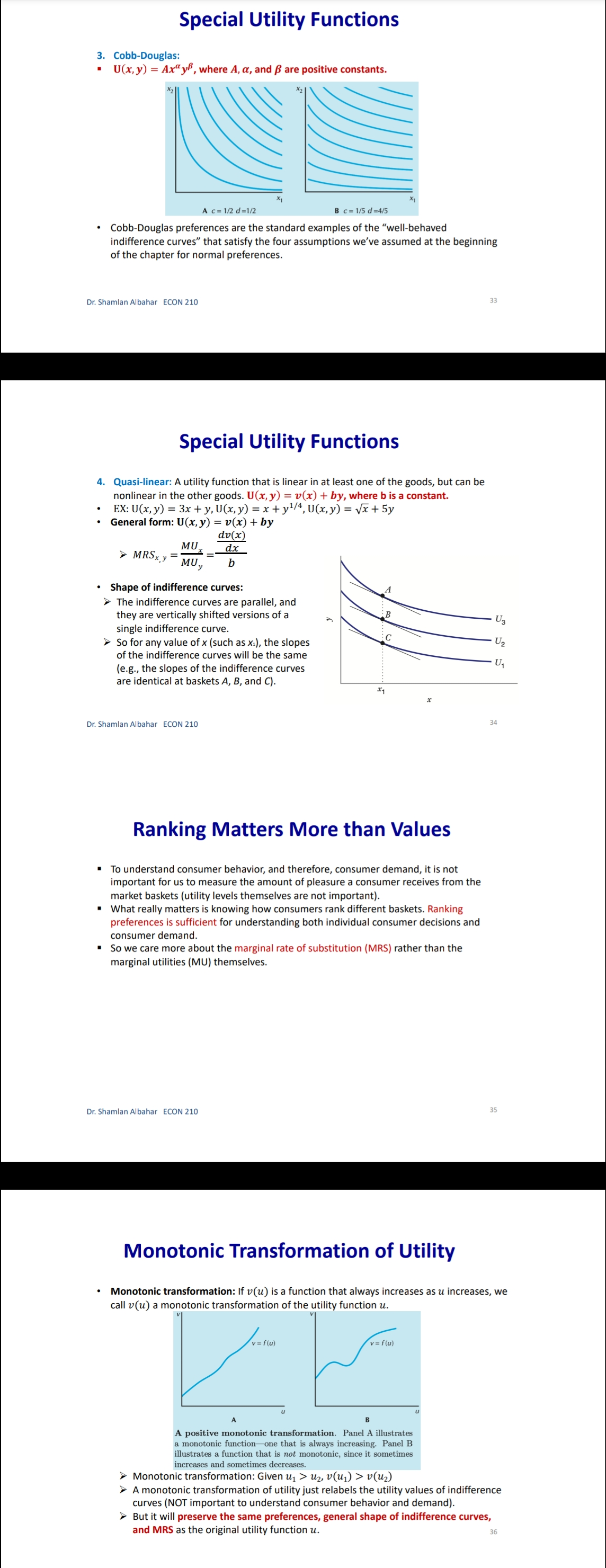
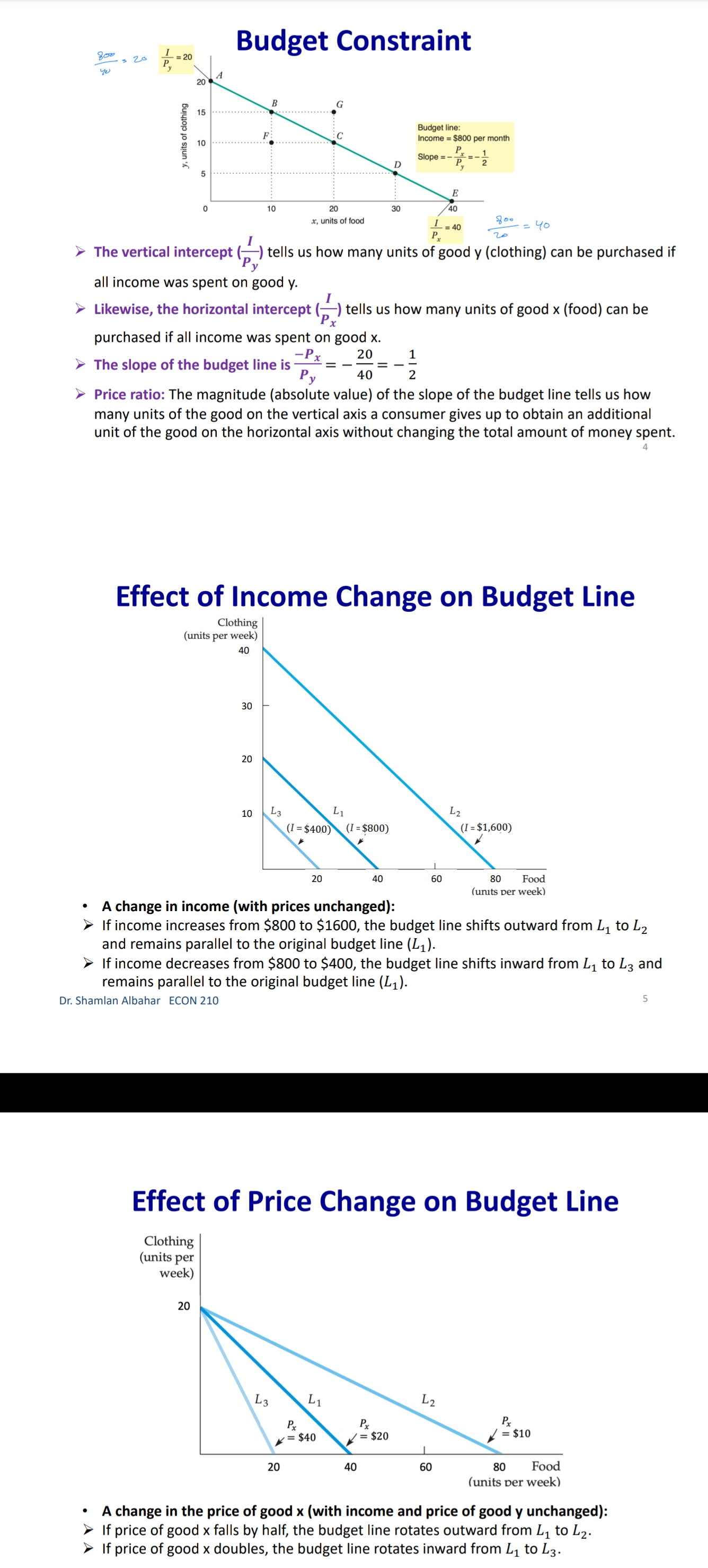
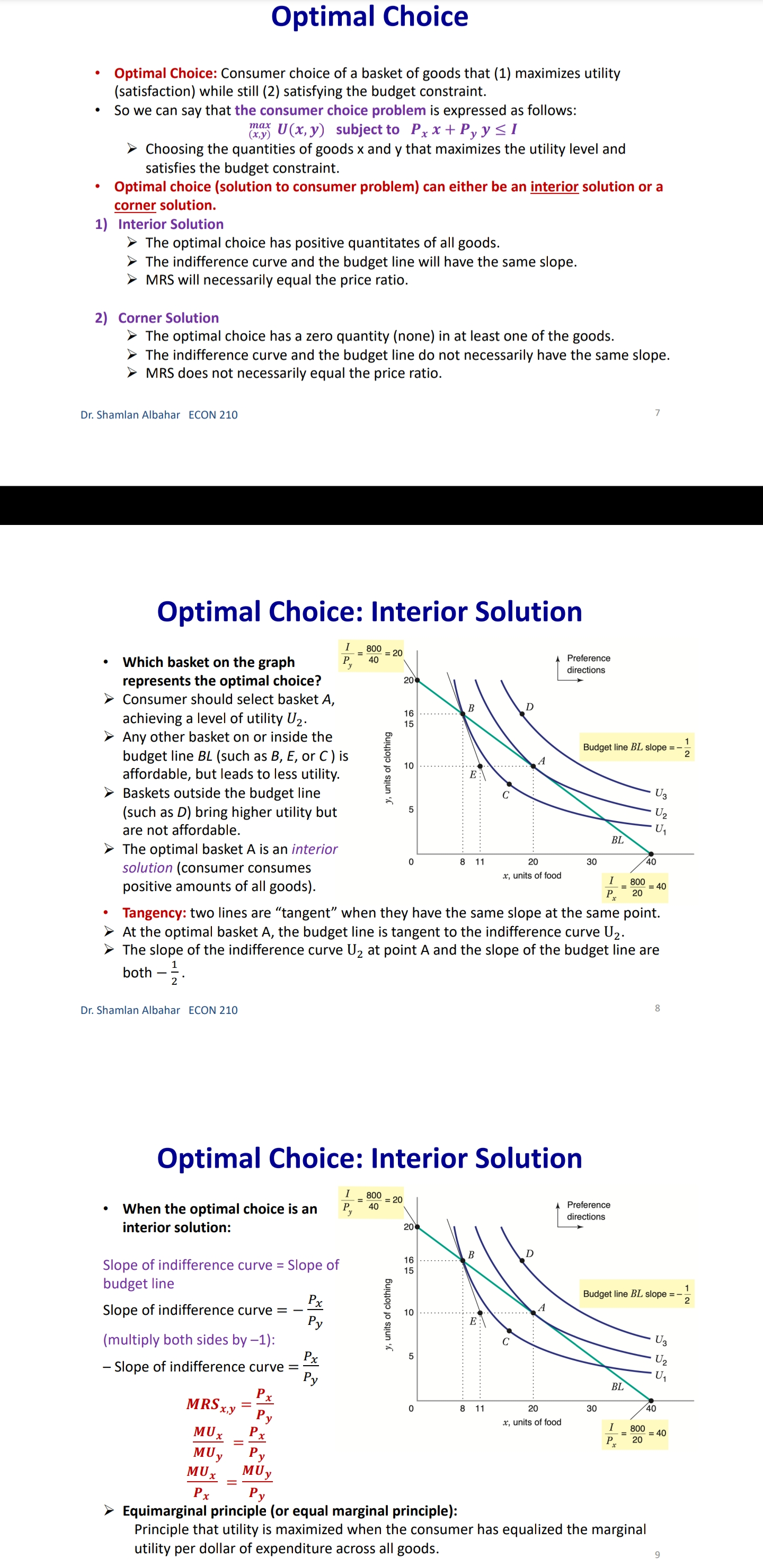
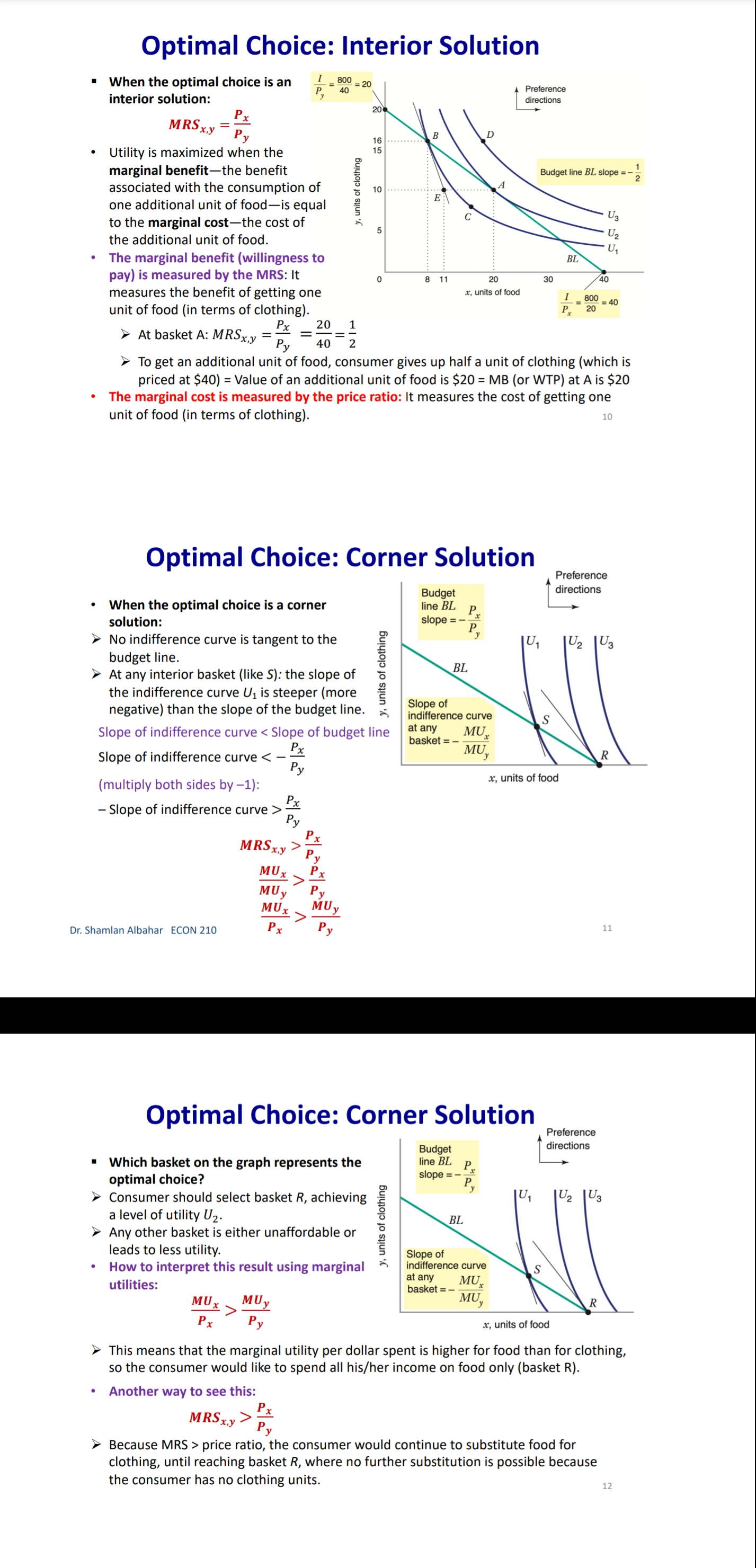
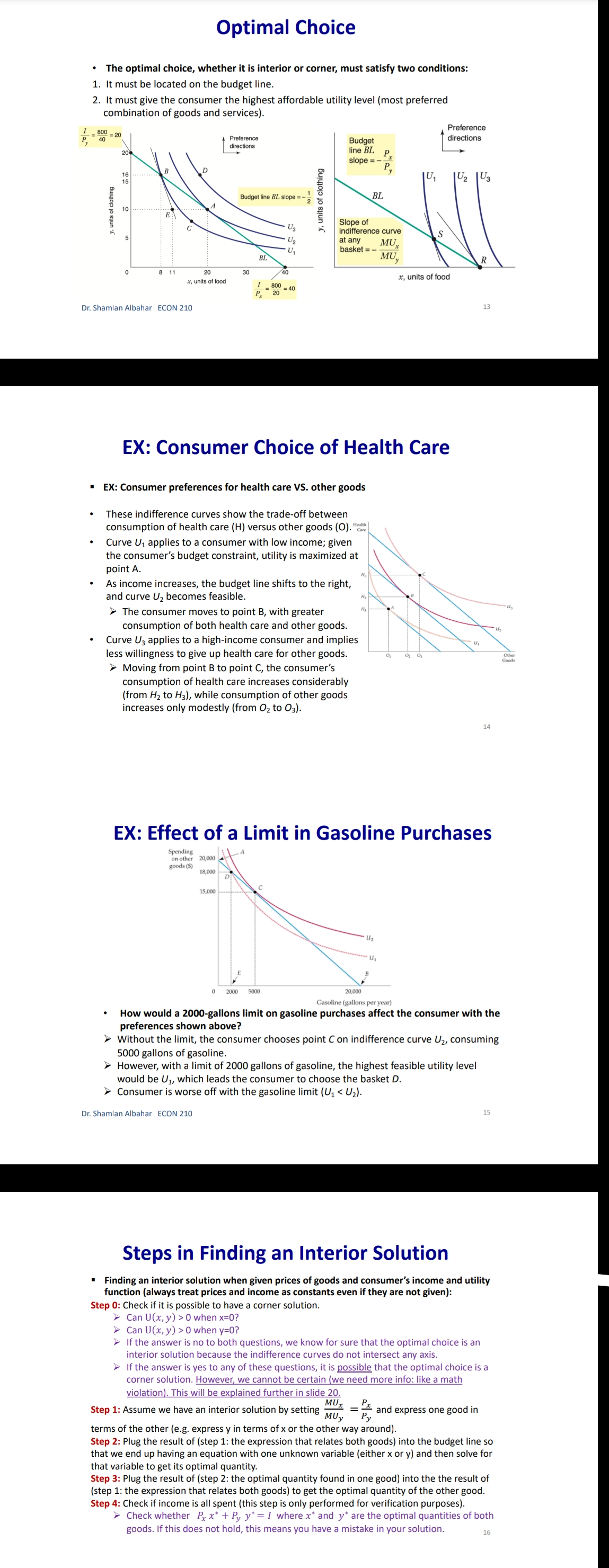
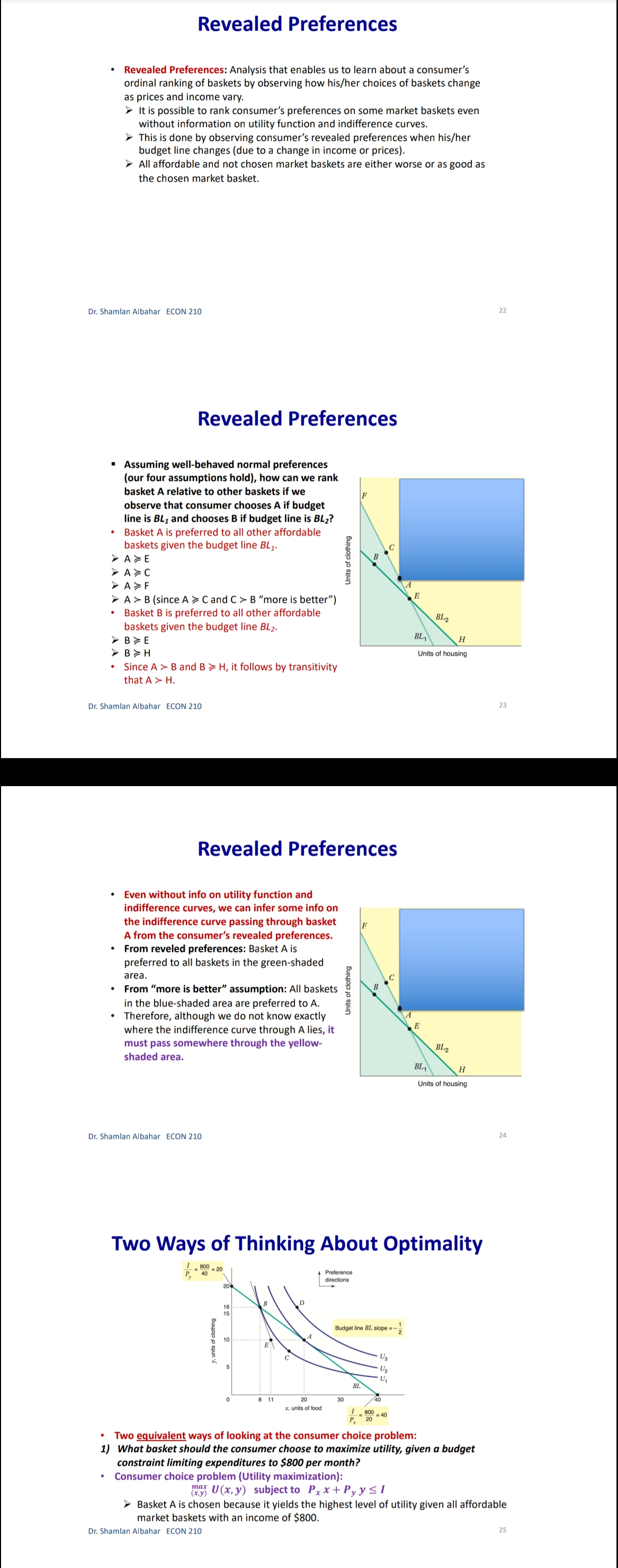
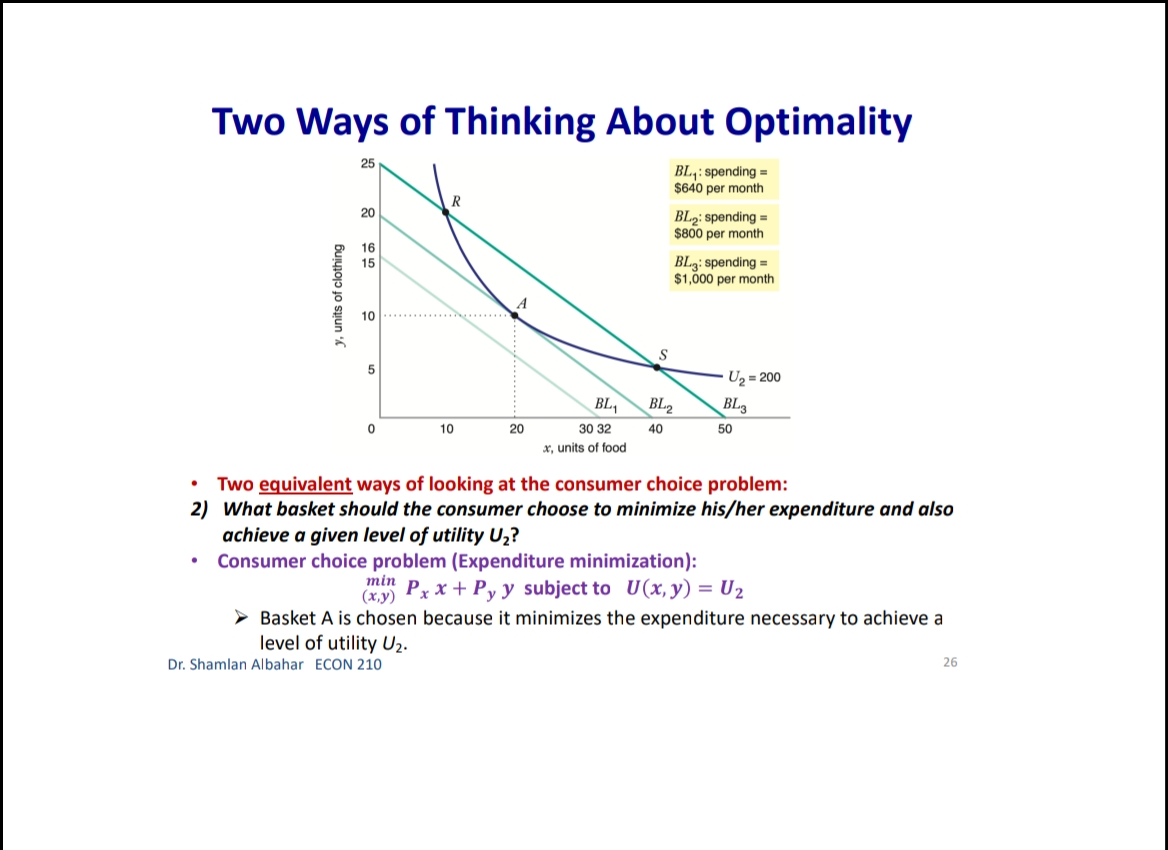
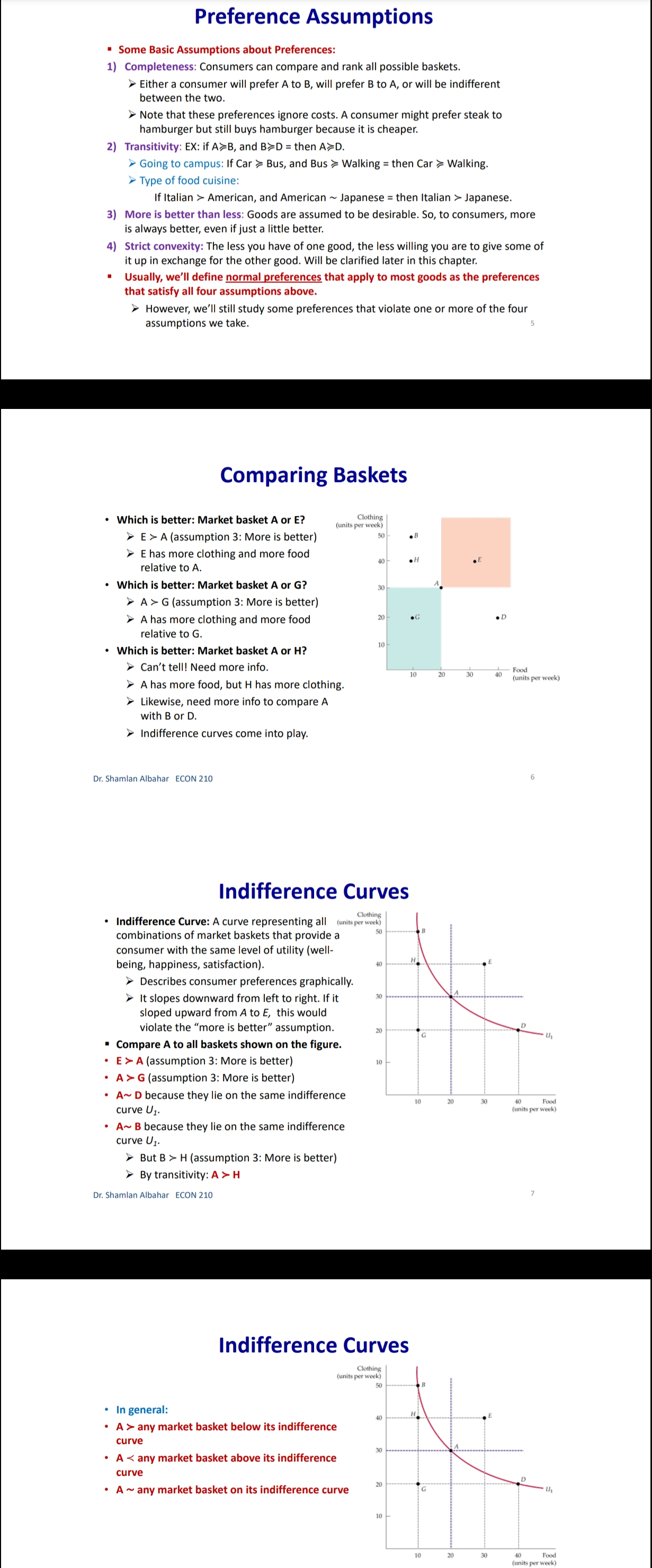
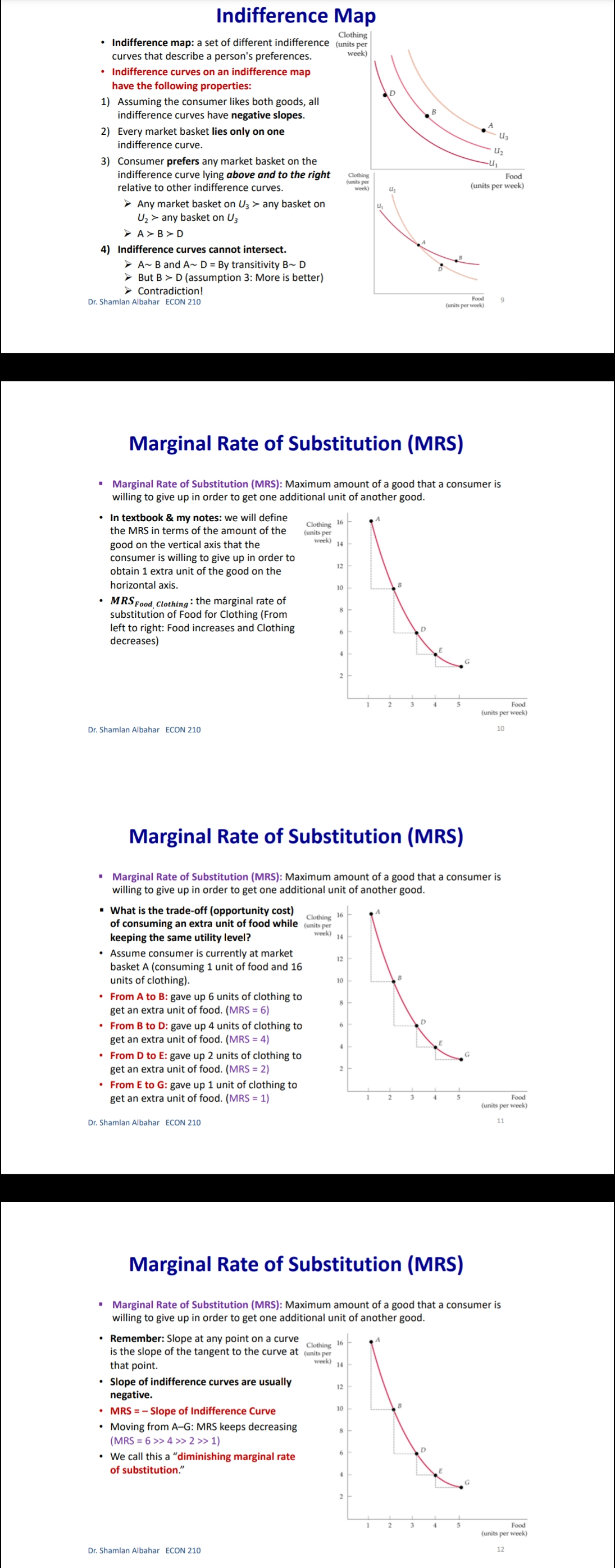
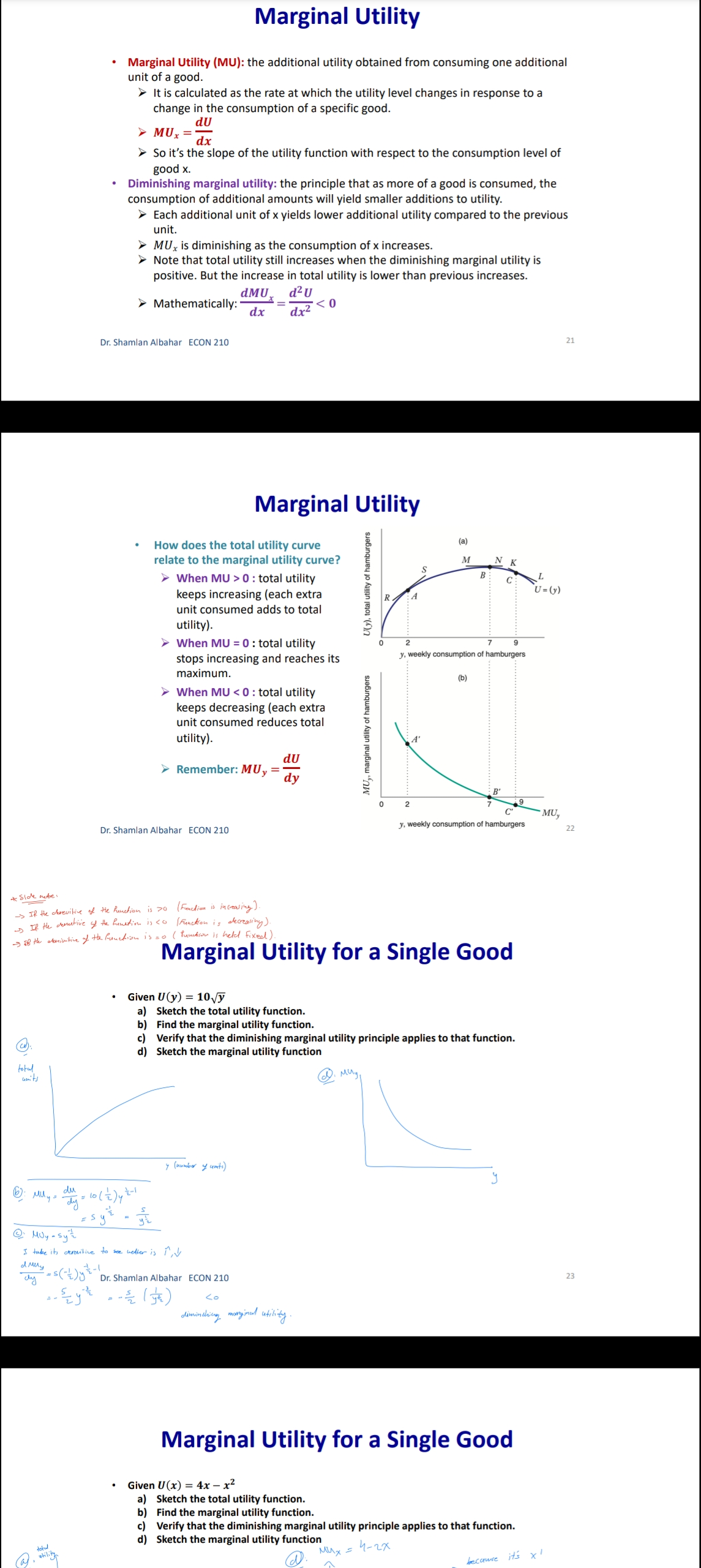
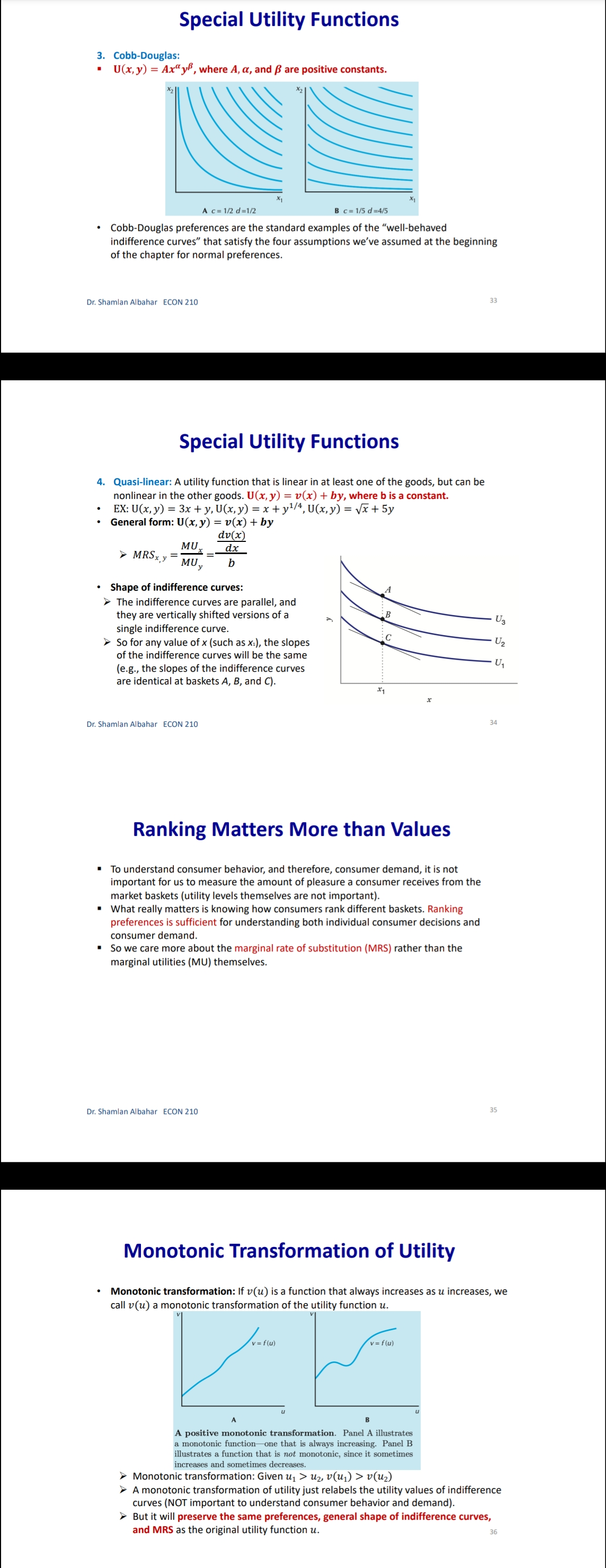
Chapter 3: Consumer Behavior Part B: Budget Constraint & Optimal Choice Dr. Sham/an Wa/eed Albahar ECON 210 (Microeconomic Theory) Department of Economics, College of Business Administration Kuwait University Fall 2022 Budget Constraint ' Notation: x: quantity of good x y: quantity of good y Px: price of good x P}, : price of good y I: total income What condition defines the set of all affordable market baskets? P, x + P}, y S I 'r We call this \"the budget constraint." iv Budget Constraint: Defines the set of all affordable baskets that a consumer can purchase given his/her available income. What condition defines the case when the consumer spends a_|l his/her income on goods x and y? PX x + Py y 2 I '9 We call this \"the budget line" I Budget Line: Defines the set of baskets that a consumer can purchase when spending all of his/her available incomes Dr Shamlan Albahar ECON 210 Budget Constraint . Example: I p ' Assume the price of good x (food) $20 per ' m 1 unit, and the price of good y (clothing) $40 per unit. Assume consumer's income is $800. - Budget Constraint: 20x + 40y S 800 ' Budget Line: 20x + 40y : 800 "r Consumer can buy any basket on or inside a m 2\" m m the budget line: Baskets AF t mm\". , 'r Baskets AE expends all consumer's income ($800). 'r Basket F only costs the consumer $600 'r Consumer cannot buy a basket outside the budget line, such as basket 6, which costs more than the available income (Costs $1000 and available income is $800). =20 I5 Budqeilme name = saw per month Sin , PU ' IJ Db 1', 7 3 \\ unils nl earning - :Ao Budget Constraint 80% , 20 =20 you B G 15 . . . .......... . . . . .......... Budget line: y, units of clothing C . . . . ............" Income = $800 per month 10 . . . .......... Slope = - x = - 2 D 5 ................... . . . . 10 20 30 x, units of food =40 $00 = 40 P x > The vertical intercept ( ) tells us how many units of good y (clothing) can be purchased if all income was spent on good y. Likewise, the horizontal intercept ( ) tells us how many units of good x (food) can be purchased if all income was spent on good x. > The slope of the budget line is SPx 20 Py 40 2 > Price ratio: The magnitude (absolute value) of the slope of the budget line tells us how many units of the good on the vertical axis a consumer gives up to obtain an additional unit of the good on the horizontal axis without changing the total amount of money spent. Effect of Income Change on Budget Line Clothing (units per week) 40 30 20 10 L3 L1 L2 (1 = $400) (1 =$800) (1 = $1,600) 20 60 80 Food (units per week) . A change in income (with prices unchanged): If income increases from $800 to $1600, the budget line shifts outward from L, to L2 and remains parallel to the original budget line (L1). If income decreases from $800 to $400, the budget line shifts inward from L1 to L3 and remains parallel to the original budget line (L1). Dr. Shamlan Albahar ECON 210 Effect of Price Change on Budget Line Clothing (units per week) 20 L3 L1 L2 Px Px Px If price of good x falls by half, the budget line rotates outward from L, to L2. > If price of good x doubles, the budget line rotates inward from L1 to L3.Optimal Choice - Optimal Choice: Consumer choice of a basket of goods that (1) maximizes utility (satisfaction) while still (2) satisfying the budget constraint. - So we can say that the consumer choice problem is expressed as follows: (\"$5 U(x, y) subject to PX x + Py y S I > Choosing the quantities of goods x and y that maximizes the utility level and satisfies the budget constraint. - Optimal choice (solution to consumer problem) can either be an M solution or a M solution. 1) Interior Solution >> The optimal choice has positive quantitates of all goods. iv The indifference curve and the budget line will have the same slope. T MRS will necessarily equal the price ratio. 2) Corner Solution >> The optimal choice has a zero quantity (none) in at least one of the goods. 3 The indifference curve and the budget line do not necessarily have the same slope. S MRS does not necessarily equal the price ratio. Dr. Shamlan Albahar ECON 210 Optimal Choice: Interior Solution 1 800 Frelerence directions 20 - which basket on the graph P) _ 4 _ represents the optimal choice? > Consumer should select basket A, achieving a level of utility U2. > Any other basket on or inside the budget line BL (such as B, E, or C) is affordable, but leads to less utility. > Baskets outside the budget line (such as D) bring higher utility but 5 are not affordable. > The optimal basket A is an interior solution (consumer consumes x) uni'smod positive amounts ofall goods). ==4o Tangency: two lines are \"tangent\" when they have the same slope at the same point. At the optimal basket A, the budget line is tangent to the indifference curve U2. The slope of the indifference curve U2 at point A and the slope of the budget line are 1 both ;. mm Budget line EL slope :7; y, units oi clothing 3 VV Dr. Shamlan Albahar ECON 210 Optimal Choice: Interior Solution 1 7 800 7 _ _ Preference directions 20 - when the optimal choice is an P) '0 interior solution: Slope of indifference curve = Slope of ma) (multiply both sides by l): budget line .3 ' P % Budget line EL slope :7 E Slope of indifference curve = x g 10 Py .2 c 3 . . Px U2 Slope of Indifference curve = Py \"I PX MRSx'y = y o .un'ls ollood MU, P, f ' If =:%0=40 = \\. MU), P), MUI _ MUy P, _ Py > Equimarginal principle (or equal marginal principle): Principle that utility is maximized when the consumer has equalized the marginal utility per dollar of expenditure across all goods. Slope of indifference curve m -40 unit offood (in terms of clothing). Pr 7 2 7 t , _ _ _ l r At basket A. MRS,\"y Py 40 2 F To get an additional unit of food, consumer gives up half a unit of clothing (which is priced at $40) = Value of an additional unit of food is $20 = MB (or WTP) at A is $20 The marginal cost is measured by the price ratio: It measures the cost of getting one unit of food (in terms of clothing). Optimal Choice: Corner Solution Preference Budget mil)\" when the optimal choice is a corner line BL P solution: Slope = - PI No indifference curve is tangent to the 'Y budget line: At any interior basket (like 5): the slope of the indifference curve U1 is steeper (more negative) than the slope of the budget line. u2 U3 y, units of clothing Slope of indifference curve P basket=_ VII; Slope of indifference curve P' y MRS > P' xy Py MU, > 5 MU}, Py MUJr MUy Dr Shamlan Albahar ECON 210 P2: Py Optimal Choice: Corner Solution P ' Budget directions l' 31: me Pr SID e:' p P Which basket on the graph represents the optimal choice? Consumer should select basket R, achieving a level of utility Uz. Any other basket is either unaffordable or leads to less utility: How to interpret this result using marginal utilities: Slope of indierence curve at any MU basket = 7 ' MUy y, units ol clothing MU MU x > .V PX Py x. units of iced This means that the marginal utility per dollar spent is higher for food than for clothing, so the consumer would like to spend all his/her income on food only (basket R). Another way to see this: PX MRSva > Py Because MRS > price ratio, the consumer would continue to substitute food for clothing, until reaching basket R, where no further substitution is possible because the consumer has no clothing units, Optimal Choice ~ The optimal choice, whether it is interior or corner, must satisfy two conditions: 1. It must be located on the budget line. 2. It must give the consumer the highest affordable utility level (most preferred combination ofgoods and services). , m Pieieierice ,1, = on '2\" Fielerence Budge, directions __ directions We BL P 2D ' slope = , l p oi in E I is g i2 2 2 5 stage. mar some; g g in g 3 =1 Sione oi ; ' " inoiiiararioa curve 5 i 2 al any MU c', basket = e ' r o a ,. Wiimm / x. units oi load I ; mo .40 P 20 or SliufiildllAllJAlidY ECON 210 EX: Consumer Choice of Health Care I EX: Consumer preferences for health care VS. other goods - These indifference curves show the trade-off between consumption of health care (H) versus other goods (0). \" - Curve U1 applies to a consumer with low income; given the consumer's budget constraint, utility is maximized at point A. - As income increases, the budget line shifts to the right, and curve U2 becomes feasible. 'r The consumer moves to point B, with greater ' " consumption of both health care and other goods. \ xe. - Curve U3 applies to a high-income consumer and implies less willingness to give up health care for other goods. ii 'r Moving from point B to point C, the consumer's consumption of health care increases considerably (from H; to H3), while consumption of other goods increases only modestly (from 02 to 03). EX: Effect of a Limit in Gasoline Purchases t,. ,i lsihh '. l i r r ,... . How would a moo-gallons limit on gasoline purchases affect the consumer with the preferences shown above? 'r Without the limit, the consumer chooses point C on indifference curve U2, consuming 5000 gallons of gasoline. r However, with a limit of 2000 gallons of gasoline, the highest feasible utility level would be U1, which leads the consumer to choose the basket D. r Consumer is worse off with the gasoline limit (u1 0 when x:0? r can U(X,y) > 0 when y:0? r Ifthe answer is no to both questions, we know for sure that the optimal choice is an interior solution because the indifference curves do not intersect any axis r lfthe answer is yes to any of these questions, it is possible that the optimal choice is a corner solution. However we cannot be certain [we need more info like a math violation . This will be explained further in slide 20. p MU Step 1: Assume we have an interior solution by setting MUX = PX and express one good in y y terms of the other leg express y in terms of x or the other way around). Step 2: Plug the result of (step 1: the expression that relates both goods) into the budget line so that we end up having an equation with one unknown variable (either x or y) and then solve for that variable to get its optimal quantity. Step 3: Plug the result of (step 2: the optimal quantity found in one good) into the the result of {step 1: the expression that relates both goods) to get the optimal quantity of the other good. Step 4: Check if income is all spent (this step is only performed for verification purposes]. r Check whether 17, x' + P, y' :1 where x and y' are the optimal quantities of both goods. lfthis does not hold, this means you have a mistake in your solution Revealed Preferences O Revealed Preferences: Analysis that enables us to learn about a consumer's ordinal ranking of baskets by observing how his/her choices of baskets change as prices and income vary. '5' It is possible to rank consumer's preferences on some market baskets even without information on utility function and indifference curves. '5' This is done bv observing consumer's revealed preferences when his/her budget line changes (due to a change in income or prices). Xv All affordable and not chosen market baskets are either worse or as good as the chosen market basket. Dr Shamlan Aibahar ECON 210 Revealed Preferences I Assuming wellabehaved normal preferences (our four assumptions hold), how can we rank basket A relative to other baskets if we observe that consumer chooses A if budget line is BL, and chooses B if budget line is 8in O Basket A is preferred to all other affordable baskets given the budget line BL}. g 'r A z E L; *r A z c g *r A > r 3 'r A > B [since A a C and C > 8 \"more is better\") O Basket B is preferred to all other affordable baskets given the budget line 31;. a e E a e H Units or housing Since A > B and B > H, it follows by transitivity that A > H. . V'V' Dr Shamlon Albalmr ECON 210 Revealed Preferences . Even without info on utility function and indifference curves, we can infer some info on the indifference curve passing through basket A from the consumer's revealed preferences. . From reveled preferences: Basket A is preferred to all baskets in the gree n-shad ed area. O From "more is better" assumption: All baskets in the blue-shaded area are preferred to A. O Therefore, although we do not know exactlv where the indifference curve through A lies, it must pass somewhere through the yellow shaded area. Units oi clolhing Unils in housing Dr Shamlan Albahnr ECON 210 Two Ways of Thinking About Optimality I 1 m : ,iy .o 9" . Pralerance diiaclius l u \"is; \"75:7 saw ll iv 2 w i was a coming, . unit: oi food I coo = = r I' 2 . Two eguivalent ways of looking at the consumer choice problem: 1} What basket should the consumer choose to maximize utility, given a budget constraint limiting expenditures to $800 per month? - Consumer choice problem (Utility maximization): {1"}: Why) subjectto P, x + Py y S I 'r Basket A is chosen because it yields the highest level of utility given all affordable market baskets with an income of 3800' Dr Shamlziri Albahar ECON 210 Two Ways of Thinking About Optimality 25 BL, : spending = $640 per month 20 BL2: spending = $800 per month 16 BLig: spending = $1,000 per month y, units of clothing A 10 . . . .. . . ." S 5 U2 = 200 BL BL 2 BLa 10 20 30 32 40 50 x, units of food . Two equivalent ways of looking at the consumer choice problem: 2) What basket should the consumer choose to minimize his/her expenditure and also achieve a given level of utility Uz? Consumer choice problem (Expenditure minimization): min Px x+ Py y subject to U(x, y) = U2 > Basket A is chosen because it minimizes the expenditure necessary to achieve a level of utility U2. Dr. Shamlan Albahar ECON 210 26Chapter 3: Consumer Behavior Part A: Consumer Preferences & Utility Dr. Sham/an Waleed Albahar ECON 210 (Microeconomic Theory) Department of Economics, College of Business Administration Kuwait University Fall 2022 Consumer Behavior - Theory of consumer behavior: Describes how consumers allocate incomes among different goods and services to maximize their utility (well-being, happiness, satisfaction). - Consumer behavior is best understood in three distinct steps: 1) Consumer Preferences r We should understand how a typical consumer prefers one good to another. 2) Budget Constraints r Given products prices, a consumer has limited incomes = limited potential of purchases 3) Consumer Choices r Putting consumer preferences and budget constraints together: what combination of goods and services maximize the consumer's utility? r Understanding consumer choice will help us understand demand. - Are consumers always rational? r No (e.g. bad judgment, emotional, hasty) = BehaVIoral Economics (more realistic assumptions) r Our model assumes rationality = simplifies analysis and consistent with much (but not all) of what we actually observe. consumer Preferences ' First step in studying consumer behavior: Consumer Preferences ' Market Basket (or bundle): List with specific quantities of one or more goods. MARKET BASKET UNlTS OF FOOD UNITS OF CLOTHING A 20 30 B 10 50 D 40 20 E 30 40 G 10 20 H 10 40 ' To explain the theory of consumer behavior, we will ask whether consumers prefer one market basket to another. ' We'll find out later that consumers will choose the market basket that gives them the highest level of utility (well-being, happiness, satisfaction) given their limited incomes and the prices they face. Dr. Shamlan Albahar ECON 210 Preference Notation ' Preference Notation: A > B: Consumer strictly prefers A to B (100% consumer will choose A over B) A > B: Consumer weakly prefers A to B (Consumer either chooses A over B or is indifferent between them) A ~ B: Consumer is indifferent between the two baskets (Any ofthese baskets gives the consumer the same level of utility) Preference Assumptions I Some Basic Assumptions about Preferences: 1) Completeness: Consumers can compare and rank all possible baskets. P Either a consumer will preferAto B, will prefer B to A, or will be indifferent between the two. r Note that these preferences ignore costs. A consumer might prefer steak to hamburger but still buys hamburger because it is cheaper. 2) Transitivity: EX: ifA>B, and B>D = then A>D. r Going to campus: If Car > Bus, and Bus > Walking = then Car > Walking. r Typo of food cuisine: If Italian > American, and American ~ Japanese = then Italian > Japanese. 3) More is better than less: Goods are assumed to be desirable. So, to consumers, more is always better, even if just a little better. 4) Strict convexity: The less you have of one good, the less willing you are to give some of it up in exchange for the other good. Will be clarified later in this chapter. I Usually, we'll define normal preferences that apply to most goods as the preferences that satisfy all four assumptions above. > However, we'll still study some preferences that violate one or more of the four assumptions we take. Comparing Baskets - which is better: Market basket A or E? .......~,.:.\"{f'.'l'i 'r E > Alassumption 3: More is better) -I' 'r E has more clothing and more food relative to A. - which is better: Market basket A or G? t. '. 'r A > G (assumption 3: More is better) '7 A has more clothing and more food '\" " "' relative to G. - which is better: Market basket A or H? 'r Can't tell! Need more info. 'r A has more food, but H has more clothing. '7 Likewise, need more info to compare A with B or D. 'r Indifference curves come into play. In .H .1 Dr ShnmlnnAlbnhnr ECON 210 Indifference Curves - Indifference Curve: A curve representing all combinations of market baskets that provide a consumer with the same level of utility (wellr being, happiness, satisfaction). w r Describes consumer preferences graphically. 'r It slopes downward from left to right. If it sloped upward from A to E, this would violate the \"more is better" assumption. - Compare Ato all baskets shown on the figure. - E >A (assumption 3: More is better) I' - A > G (assumption 3: More is better) - A~ D because they lie on the same indifference .. .. . curve U). m... ,.. - A~ B because they lie on the same indifference curve U). 'r But B > H (assumption 3: More is better) 'r By transitivity: A > H Dr SimmlnnAlbnhnr MON 210 Indifference Curves - In general: - A > any market basket below its indifference curve - A any basket on U2 > any basket on U > A > B > D 4) Indifference curves cannot intersect. A~ B and A~ D = By transitivity B~ D > But B > D (assumption 3: More is better) Contradiction! Dr. Shamlan Albahar ECON 210 (units per week) Marginal Rate of Substitution (MRS) Marginal Rate of Substitution (MRS): Maximum amount of a good that a consumer is willing to give up in order to get one additional unit of another good. In textbook & my notes: we will define the MRS in terms of the amount of the Clothing (units per good on the vertical axis that the week) 14 consumer is willing to give up in order to obtain 1 extra unit of the good on the horizontal axis. . MRS Food Clothing : the marginal rate of substitution of Food for Clothing (From left to right: Food increases and Clothing decreases) Food (units per week) Dr. Shamlan Albahar ECON 210 10 Marginal Rate of Substitution (MRS) Marginal Rate of Substitution (MRS): Maximum amount of a good that a consumer is willing to give up in order to get one additional unit of another good. . What is the trade-off (opportunity cost) of consuming an extra unit of food while (units per keeping the same utility level? week) 14 Assume consumer is currently at market basket A (consuming 1 unit of food and 16 units of clothing). From A to B: gave up 6 units of clothing to get an extra unit of food. (MRS = 6) . From B to D: gave up 4 units of clothing to get an extra unit of food. (MRS = 4) . From D to E: gave up 2 units of clothing to get an extra unit of food. (MRS = 2) From E to G: gave up 1 unit of clothing to get an extra unit of food. (MRS = 1) (units per week) Dr. Shamlan Albahar ECON 210 11 Marginal Rate of Substitution (MRS) " Marginal Rate of Substitution (MRS): Maximum amount of a good that a consumer is willing to give up in order to get one additional unit of another good. Remember: Slope at any point on a curve Clothing is the slope of the tangent to the curve at (units per that point. week) 14 . Slope of indifference curves are usually 12 negative. . MRS = - Slope of Indifference Curve Moving from A-G: MRS keeps decreasing (MRS = 6 > > 4>> 2>> 1) We call this a "diminishing marginal rate of substitution." Food (units per week) Dr. Shamlan Albahar ECON 210 12MR5 and Convexity I Strictly Convex Preferences (4m assumption in slide 5 Preferences Assumptions): - The less you have of one good, the less willing you are to give some of it up in exchange for the other good. 'r Another way of describing this principle: consumers generally prefer balanced market baskets to market baskets that contain all of one good and none of another. 7 Checking strict convexity: should have diminishing MRS. I How do we know if the indifference curve is '3\" strictly convex (we have strictly convex preferences)? i: r Diminishing MRS(6 >>4>>2>> 1| N r 0r another way to check this: Slope of indifference curves gets less and less negative (Slope of indifference curve : 6 >> 4 >> 2 >> 1) i 1 -_ i : mi MW ~\\\\il Dr. Shamlan Albahar ECON 210 Mustang V5. Explorer I Preferences for automobile attributes (e.g. acceleration. interior space) can be described by indifference curves. I Each indifference curve shows the combination of acceleration and interior space that give the same utility level. I Ford Mustang Vs. Ford Explorer cm. Ford Mustang Ford Explorer Dr. Shamlan Albahar ECON 210 Mustang V5. Explorer 2n- > Buyers of Ford Mustang like seed. '9 Buyers of Ford Explorer like spaced They are willing to give up much interior They are less willing to give up interior space for additional acceleration space for additional acceleration. [mafii (minim 12H l1l1 mi mu iii no so m i 7i u: i l l l l m um l'ill mu m natiwnm an my my my my mama\" lawman, itmpwi [a] bi Dr. Shamlan Albahar ECON 210 MRS & Shape of Indifference Curve I Different shapes of indifference curves imply different preferences and MRS. - Sketch the different shapes of the indifference curves given the following scenarios: 3) MRS\" is diminishing. i' ., i . .. .. .. b) MRS\" is increasing. ' ' a c) MRS\" = a, where am. i . J ' ll d) MRS\" = D ' '1 y e) was,y = no (infinity) ; . H ' .. ' ~ ' ii. , ' Substitutes and Compliments I Two goods are substitutes when an increase in the price of one leads to an increase in the demand of the other. These goods are usually used in place of one another. Meanwhile, the consumer may prefer one over the other (e.g. Pepsi and )uice). > Extreme: Two goods are perfect substitutes when a consumer is completely indifferent between the two goods (e.g. Pepsi and Cola). I Two goods are complements when an increase in the price of one leads to a decrease in the demand of the other. These goods are usually used together. Meanwhile, a consumer may consume them separately and still get some utility (e.g. Cake and Cappuccino). 'r Extreme: Two goods are perfect complements when two goods are always consumed together in fixed proportions. No extra utility to consumer if they're not consumed together (e.g. car and gasoline). I Two extreme examples where we do not have strictly convex preferences (violation of assumption 4 on normal preferences): perfect substitutes and perfect compliments (In both: MRS not diminishing). r Note the word "Perfect\" means unusual extreme cases. or SlianilaiiAlbahai ECON 210 Perfect Substitutes I when are two goods perfect substitutes? (a) lunch Siibstitutus 'r Whenever a consumer is completely indifferent APP!e between two goods. 4mg; 'r Or we can say whenever MRS = Constant - EXl: Sarah is always indifferent between a glass of orange juice and a glass of Apple juice. I MRSomnm'Apple: the marginal rate of substitution oforange Juice for apple Juice (more orange juice and less apple juice) 'r MRS=1 (constant) - EXZ: Hamad is always indifferent between one 16 1 3 4 GB memory card and two 8 GB cards because Orange )uKE (ginsses) both have the same memory capacity. 'r' MRS16 EH \"3: the marginal rate of substitution of 16 GB memory card for an 8 GB memory card (16 GB cards increase and 8 GB cards decrease] r M RS=2 (constant) r Sketch the indifference curve Dr Shainlan Albahar ECON 210 Perfect Compliments (m Perm tnmpicmenrs . L i When are two goods perfect compliments? J\": Whenever two goods are always consumed together in fixed proportions. Or we can say whenever MR5 = zero or infinite EX: What if you own a shoe store that only sells left pairs? htt 5: www. outube.com watch?v=bf XuVPle3M P An additional left shoe gives no extra utility unless we have the matching right shoe. D ' j 1 J in titstioes - MRSmHmSM, LEI-\"ME : the marginal rate of substitution of a right shoe for a left 3 shoe (right shoes increase and left shoes decrease) r To get MRS: How many left shoes are we willlng to give up in get an extra right shoe? r If right shoes > left shoes: We will not give up any left shoe to get an extra unneeded right shoe. 50 MRS: zero. If right shoes right shoes Utility I Utility = wellrbeing, happiness, satisfaction. r It can be represented by a numerical score representing the satisfaction (happiness) that a consumer gets from a given market basket. I Utility function: a mathematical function that assigns a level of utility to any market basket. I EX: Draw three indifference curves with utility levels of 25, 50, and 100 associated with the following utility function: U(F, C) = FC , How to draw them. Given the utility level of interest (eg. U=25), pick arbitrary values of C and then solve for F such that U(F, C) = FC (or do the opposite: C and F). n iii-mo mm y. r nu xi in i: find \"WWW.\" Dr Shamlan Albahar ECON 210 Marginal Utility Marginal Utility (MU): the additional utility obtained from consuming one additional unit of a good. > It is calculated as the rate at which the utility level changes in response to a change in the consumption of a specific good. >MUX = du dx > So it's the slope of the utility function with respect to the consumption level of good x. Diminishing marginal utility: the principle that as more of a good is consumed, the consumption of additional amounts will yield smaller additions to utility. > Each additional unit of x yields lower additional utility compared to the previous unit. > MUx is diminishing as the consumption of x increases. Note that total utility still increases when the diminishing marginal utility is positive. But the increase in total utility is lower than previous increases. dMU, dzu > Mathematically:- dx dx2 Dr. Shamlan Albahar ECON 210 21 Marginal Utility How does the total utility curve a) relate to the marginal utility curve? M > When MU > 0 : total utility B : U(y), total utility of hamburgers keeps increasing (each extra U = () R unit consumed adds to total utility). No ......... > When MU = 0 : total utility 9 stops increasing and reaches its y, weekly consumption of hamburgers maximum. (b > When MU Take the partial derivative: the derivate of the function with respect to the variable of interest, while treating other variables as arbitrary constants. Given U(x, y) >MUx = du(x,y) . : taking the derivate w.r.t. x while treating y as a constant. dx > MU, = du(x,y) . : taking the derivate w.r.t. y while treating x as a constant. dy MU > MRS x, y = MUy : the marginal rate of substitution of x for y, where x is the good on the horizontal axis and y is the good on the vertical axis. MU . MRS x, y = MUX * = - Slope of indifference curve MUX dy > MRS x y MUy dx Marginal Utility for Multiple Goods Given U(x, y) = 10 xy = 10 x a) Find the marginal utility function from the consumption of good x b) Find the marginal utility function from the consumption of good y. Check whether the diminishing marginal utility principle applies to the consumption of goods x and y. d) Find the marginal rate of substitution of x for y. ) . Muy = 5x2 13 / 2 Mux = du ( 10 yz ) ( z X 2) dMuy = ( 5 x z ) ( = ) y = Syz Xz = sy z dy x 3 s X y 5 ) : Muy = am = (10 x = ) (zy yes , we have diminishing marginal utility = S X Z y z = S x 2 Max sy2 x 2 ( ): Mux = syz x t MRS My May sxuye dMax = (5 y z ) ( 2 ) x z sys ye dy sx2 x 2 82 Lo =-5 yz x yes , we have diminishing marginal utility of x MRS by I how many units of y I'm willing to give up to get one extra unit y x when you ? Mrs wig Marginal Utility for Multiple Goods Given U(x, y) = Vx+ y a) Find the marginal utility function from the consumption of good x. Find the marginal utility function from the consumption of good y. Check whether the diminishing marginal utility principle applies to the consumption of goods x and y. d) Find the marginal rate of substitution of x for y- @: Mux = - MUX 21X 2 MRS ,y Muy b. Muy = - Diminishing MRS x ,y - strictly convexity preference (: dmux = 1 (- 2 ) x Z we have diminishing marginal utility of x we don't have diminishing marginal utility of y Dr. Shamlan Albahar ECON 210 27 General Rough Sketch of Indifference Curve Step 1: Find MRSx,y Step 2: Determine the general shape of the indifference curve by analyzing how MRS is changing. This is found by answering: What happens to MRSx y when x increases and y decreases? MRSx,y is diminishing! MRSx,y is increasing. > MRSx,y = a, where a>o. MRSx,y = 0~ > MRSx,y = 00 (infinity)_ Step 3: Check whether the indifference curve intersects with any of the axes. Can U(x, y) > 0 when x=0? If yes, the indifference curve intersects the y-axis. > Can U(x, y) > 0 when y=0? If yes, the indifference curve intersects the x-axis. Or. Shamlan Albahar ECON 210Marginal Utility for Multiple Goods Given U(x, y) = x1/3 y2/3 a) Does the "more is better" assumption apply to x and y? b) Find the marginal rate of substitution of x for y c) Does the diminishing MRSx,y assumption hold? d) Draw a rough sketch of the shape of the indifference curve. @ Mux = on - y' ( f x 3 ) . 3 70 @ Checking when $'s and TX = MRS x,y yes , we have diminishing MRS .y So more is better in good * ( strict convexity preference ) Muy- du - x3 ( 3 ; ] ) - 3 0 dy s grand shape , diminishing MRS xing so more is better in good y step 3 : check when it intersects the axis 6). MRS x,y # 2 x1 2 x x5 Can uyo when too ? Nom, it does not intersect the year's can uso when you ? No it does not intorrent the Kravis 2 X Dr. Shamlan Albahar ECON 210 Marginal Utility for Multiple Goods Given U(x, y) = x2 + 2y2 a) Does the "more is better" assumption apply to x and y? b) Find the marginal rate of substitution of x for y c) Does the function show strictly convex preferences? d) Draw a rough sketch of the shape of the indifference curve. @ : MU yb and XT MRS ary * = - - = 2X70 dx increasing MRS xry - >more is better for good x is we do not have diminishing MRS xiy we do not have strictly convexity preference UM - 49 70 1: General shape ( MRS xig 1 dy step 3 : wether it intersect ares - ) more is better for good y in uso when *=0? yes ) it interesent with graxis MMX 6: MRS xy uny 2x = zy can use when you ? yes of it intersect with x-axis Dr. Shamlan Albahar ECON 210 30 Special Utility Functions 1. Perfect Substitutes: . U(x, y) = ax + by where a and b are positive constants. EX1: Sarah is always indifferent between a glass of orange juice (x) and a glass of Apple juice (y). > U(x, y ) = xty MRSx y = 1 EX2: Hamad is always indifferent between one 16 GB memory card (x) and two 8 GB cards (y) because both have the same memory capacity. > U(x, y) = 2x+ y MRSx y = 2 > Sketch the indifference curve. 2. Perfect Compliments: U(x,y) = min{ax, by} where a and b are positive constants. EX: Right shoes (x) and left shoes (y). U(x1, y ) = min{x1, }} Because u(3,3)= u(3,10)= u(15,3)= only three pairs of shoes will be useful. Sketch the indifference curve. Dr. Shamlan Albahar ECON 210 Special Utility Functions 3. Cobb-Douglas: (always diminishing ) . U(x, y) = Ax' yB, where A, a, and B are positive constants. EX: U(x, y) = 3xy, U(x, y) = x1/2y1/4, U(x, y) = 3xy General form: U(x, y) = AxayB MU aAxa-lyB ax lyl > MRSx, y = ay "MU BAxayB-1 B Bx What happens to MRSx y when x is substituted for y (x increases and y decreases)? > MRSx y is diminishing. . An advantage of the Cobb-Douglas function is that we can simplify it using log monotonic transformation while still getting the same MRSx y > In(U(x, y)) = In(Ax 'yB) = In(A) + In(x*) + In(yB) = In(A) + a In(x) + B In(y) dln(U) a dx ay > MRSx y din(U) * = Bx dy The log monotonic transformation in the Cobb-Douglas function leads to the same MRS, but the marginal utilities are different than the ones associated with the original function. Dr. Shamlan Albahar ECON 210 32Special Utility Functions 3. Cobb-Douglas: I U(x, y) : Ax"y\Examples of Monotonic Transformations - Examples of monotonic transformations: a) Multiplication by a positive number: v(u) = ku for k > 0 b] Adding any constant: v(u) = u + k where k can be any number c} Log transformation: v(u) = ln(u) given that the natural log function is only defined where not] cl] Exponentials: v(u) = e\" e) Raising u to an odd power: 120:) = u\" where n is an odd integer fl Raising u to an even power if u 2 0: v(u) = u" where n is an even integer g} nth root where n is an odd integer: v{u) = 111/\" where n is an odd integer h] nth root where n is an even integer if u 2 0: v(u) = 11\"\" where n is an even integer Dr. Shamlan Altmlmr ECON 210 Applying Monotonic Transformations Why do we care about monotonic transformation? It simplifies the analysis. EX: Find MRS for the utility function: e\" The function 9\" is a monotonic transformation of the function .ry So ex?\" will preserve the same preferences, general shape of indifference curves, and MRS as the utility function xy. This means we can just find the MRS for xy and argue that ex)" is a monotonic transformation of xy so it will have the same preferences [same MRS). )'r You can check this by verifying that xy and 9-0" have the same MRS = Same preferences '2' '2' '2' \\s: x I How do we check if a function is a monotonic transformation of the other? )'r Utility functions are monotonic transformations of one another if they have the same MRS (same preferences}. Dr. Shamlan Albahar ECON 210