please answer as accurately as possible and show all work according to textbook . Thanks.
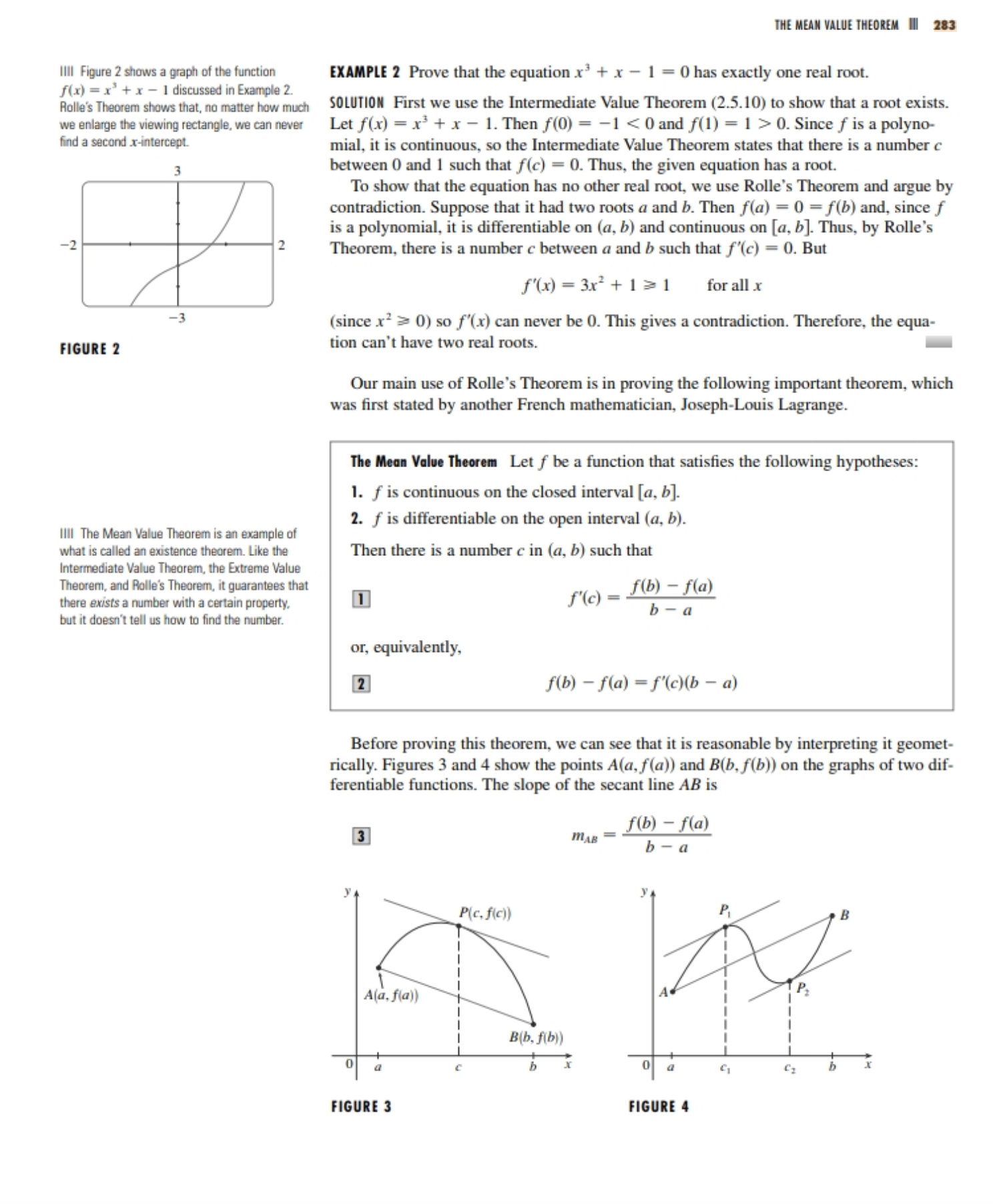
4. Let f(x) =3x3 + x 2. a. Find an interval where the function f has one root. b. Use Rolle's theorem to show that the function f has exactly one root. Hint. See Example 2 on page 283 of the textbook. THE MEAN VALUE THEOREM III 283 IIll Figure 2 shows a graph of the function f(x) = x' + x - 1 discussed in Example 2. EXAMPLE 2 Prove that the equation x' + x - 1 = 0 has exactly one real root. Rolle's Theorem shows that, no matter how much SOLUTION First we use the Intermediate Value Theorem (2.5.10) to show that a root exists. we enlarge the viewing rectangle, we can never find a second x-intercept. Let f(x) = x3 + x -1. Then f(0) = -1 0. Since f is a polyno- mial, it is continuous, so the Intermediate Value Theorem states that there is a number c between 0 and 1 such that f(c) = 0. Thus, the given equation has a root. To show that the equation has no other real root, we use Rolle's Theorem and argue by contradiction. Suppose that it had two roots a and b. Then f(a) = 0 = f(b) and, since f -2 is a polynomial, it is differentiable on (a, b) and continuous on [a, b]. Thus, by Rolle's Theorem, there is a number c between a and b such that f'(c) = 0. But f'(x) = 3x3 + 1=1 for allx (since x? > 0) so f'(x) can never be 0. This gives a contradiction. Therefore, the equa- FIGURE 2 tion can't have two real roots. Our main use of Rolle's Theorem is in proving the following important theorem, which was first stated by another French mathematician, Joseph-Louis Lagrange. The Mean Value Theorem Let f be a function that satisfies the following hypotheses: 1. f is continuous on the closed interval [a, b]. IIll The Mean Value Theorem is an example of 2. f is differentiable on the open interval (a, b). what is called an existence theorem. Like the Intermediate Value Theorem, the Extreme Value Then there is a number c in (a, b) such that Theorem, and Rolle's Theorem, it guarantees that there exists a number with a certain property. 1 f'(c) = f(b) - fla) but it doesn't tell us how to find the number. b - a or, equivalently, 2 f(b) - fla) = f'(c)(b - a) Before proving this theorem, we can see that it is reasonable by interpreting it geomet- rically. Figures 3 and 4 show the points A(a, f(a)) and B(b, f(b)) on the graphs of two dif- ferentiable functions. The slope of the secant line AB is 3 MAB = f(b) - f(a) b - a P(c, fic)) A(a, fla)) B(b, f(b)) 0 a FIGURE 3 FIGURE 4