

 please answer (b)
please answer (b)
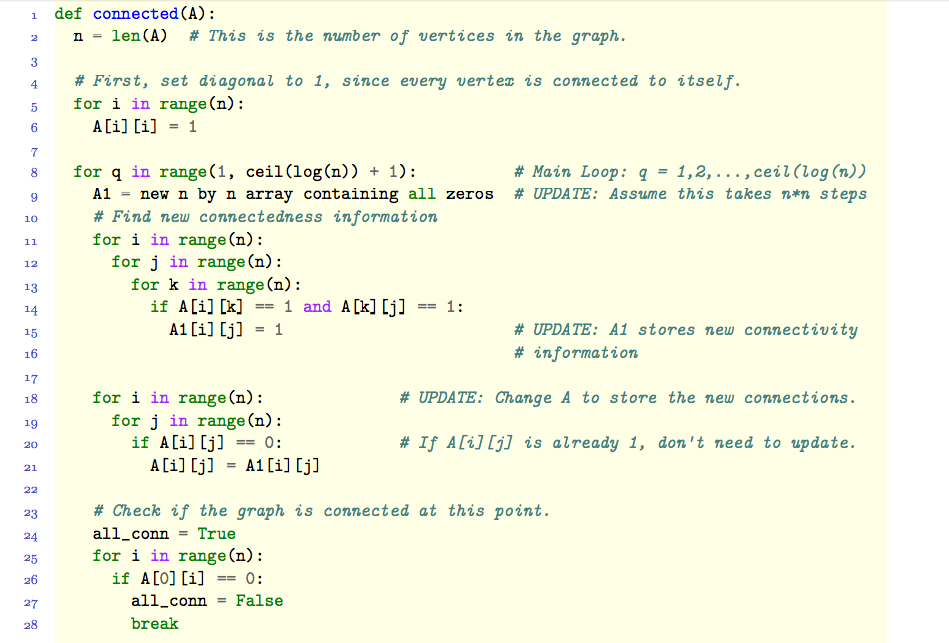
Recall that we say a graph G (V, E) is (fully) connected if and only if for every pair of vertices u, v elementof V, u and v are connected in G. Also recall (from Problem Session 11) that if the vertex set is V - {0, 1, ..., n - 1}, then we can represent a graph in a program as a two-dimensional n-by-n array A, where the entry A[i][j] is set to 1 if vertices i and j are adjacent (the edge), and 0 if they aren't. The following algorithm takes as input such an array, and returns True if the algorithm is connected, and False otherwise. def connected (A): n = len(A) # This is the number of vertices in the graph. # First, set diagonal to 1, since every vertex is connected to itself. for i in range(n): A [i] [j] = 1 for q in ranged, ceil(log(n)) + 1): # Main Loop: q = 1, 2, ..., ceil (log (n)) A1 = new n by n array containing all zeros # UPDATE: Assume this takes n*n steps #Find new connectedness information for i in range(n): for j in range(n): for k in range(n): if A[i] [k] == 1 and A[k] [j] == 1: A1[i][j] = 1 # UPDATE: A1 stores new connectivity # information for i in range(n): # UPDATE: Change A to store the new connections. for j in range(n): if A[i] [j] == 0: # If A[i] [j] is already 1, don't need to update. A[i] [j] = A1[i] [j] Check if the graph is connected at this point. all_conn = True for i in range(n): if A[0] [i] == 0: all_conn = False break if all_conn: return True # The loop has ended and *not* returned early. return False This algorithm starts with an adjacency matrix A arid continually updates the entries of A to represent new connectedness relationships between pairs of vertices. Proving correctness. To formally prove the correctness of this algorithm, we need the following predicate, where G is a graph, u and v are vertices in the graph, and d elementof N. PathLength(G, u, v, d): "there is a path in G between u and v of length at most d" Using this predicate, we can state the key property of graphs that makes the connected algorithm work: Forall G = (V, E), Forall u, v elementof V, Forall d elementof N, PathLength(G, u, v, 2d) doubleheadarrow (exist w elementof V, PathLength(G, u, w, d) A PathLength(G, w, v, d)) (a) Let n elementof Z^+ with n > 1, and consider running connected on an n-by-n adjacency matrix representing a graph G = (V, E), where V = {0, 1, ..., n - 1}. Prove by induction on q that at the end of iteration q of the Main Loop, the following is true: Forall i, j elementof V, A[i][j] = 1 rightarrow PathLength(G, i, j, 2^q) (b) Now in the same context as part (a), prove by induction on q that at the end of the iteration q of the Main Loop, the following is true: Forall i, j elementof V, A[i][j] = 0 rightarrow PathLength(G, i, j, 2^q) (You might recognize that parts (a) and (b) together prove an "if and only if.")



 please answer (b)
please answer (b)





