please answer Q5

please let me know if you need more information. thanks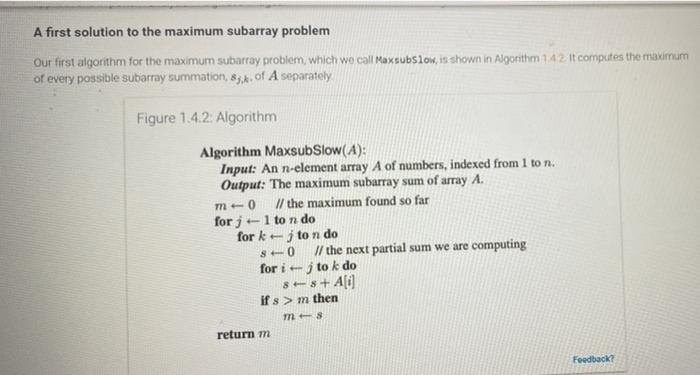

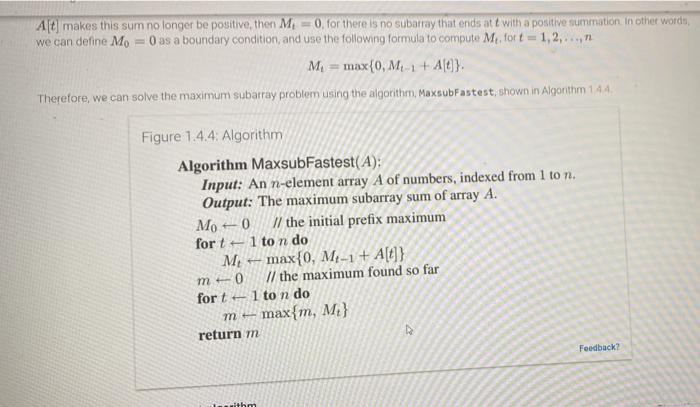
01.10) Min Max recursive algorithm 1) [10] Write a recursive alonths in pseudocode. Min Max. for finding both the minimum element and the maximum element in an array Afts Your alorithm has to make recursive call to itself only once and has to return a paire) whe the minimum cement and is the maximum element:to. it should not invoke twice to find the minimum and the maximum in the separate calls Algorithm Min-Max(A.) Input: an Array Ao nelenients Output: a pair of (ab) where is the minimum de and the maximum element 2) 120 Lomplement your algorithm fol.) in Python regar of them the minimum elements. In your algorithm in the following its A) 130, 50, 20, 70, 10, 0, 25. 100, 60.40 B) 04, 64, 24, 14.56.34.444.74 Q2 [25] For a given algorithm below. Algorithm Loop() (0) for(-1 to do (6) for todo (1) E. 1) (AIS) Count the number of primitive operations in each start (0) Lof the algorithm and Set the total number of primitive operations acted in the algorithm Assume that the variables and are created at the statement (l)automatically, woring their hidden increment statements. See the out 2) [S] Give the smallest asymptotic upper bound the ingrijih notation in terms of 18) 2011 3) [10Prove your answer is 2) by the definition of high You have to find the positive constant andre that satisfies the condition of the big oldest see the samples in the slides #22 36 and Handout O 03.110 Prove that only the definition of younge [10 Prove that with by of the Thota ar bymeme way in applying the limit function Q5.5 Maxharithms in the test is to find the way with my can modify it ta ishte find the way them) the w of the sharnay is not the would 1) 1 tly modify the Maxwastest grow the state that only hep and instead of competing different store 2) [15] Modify the Minsubastest algorithm that returns to the value of the minimum subarray ammation and the indices and that the min harray Art of value of the minimum surrayum Thening time of your rithmshold be ) 3) 120, optional Implement your Mines) - 7] in Python penting a triplet of the valus Test your algorithm with the following inputs A) 2.4.1-1.5.6.7.-24.1.2) B) -2-4-3-1.5. 6.-7.2.-4.2.2 A first solution to the maximum subarray problem Our first algorithm for the maximum subarray problem which we call Maxsubslow, is shown in Algorithm 142 It computes the maximum of every possible subarray summation, 83x of A separately Figure 1.4.2 Algorithm m Algorithm MaxsubSlow(A): Input: An n-element array A of numbers, indexed from 1 to n. Output: The maximum subarray sum of array A. 0 // the maximum found so far forj 1 to n do for k - j to n do SO // the next partial sum we are computing for i j to k do 8 + 8 + A[i] if > m then ms return m Feedback where we use the notational convention that i = 0. We can incorporate the above observations into an improved algorithm for the maximum subarray problem, called MaxsubFaster, which we show in Algorithm 143 Figure 1.4.3: Algorithm Algorithm MaxsubFaster(A): Input: An n-element array A of numbers, indexed from 1 to n. Output: The maximum subarray sum of array A. So 0 // the initial prefix sum for i=1 to n do S; -- S-1 + Ali mo // the maximum found so far for j - 1 to n do for kj to n do 8 = Sx - S-1 if > m then A ms return m Feedback Ad makes this sum no longer be positive, then M = 0, for there is no subarray that ends at with a positive summation in other words, we can define Mo = 0 as a boundary condition, and use the following formula to compute Me, fort=1,2,..., M = max{0, M + A0}, Therefore, we can solve the maximum subarray problem using the algorithm, Maxsubfastest shown in Algorithm 144 Figure 1.4.4: Algorithm Algorithm MaxsubFastest(A): Input: An n-element array A of numbers, indexed from 1 to n. Output: The maximum subarray sum of array A. 0 // the initial prefix maximum fort 1 to n do . max{0, M-1 + A[t]} mo // the maximum found so far for tl to n do max{m, M.} return m m Feedback? withm