Please answer the following questions:
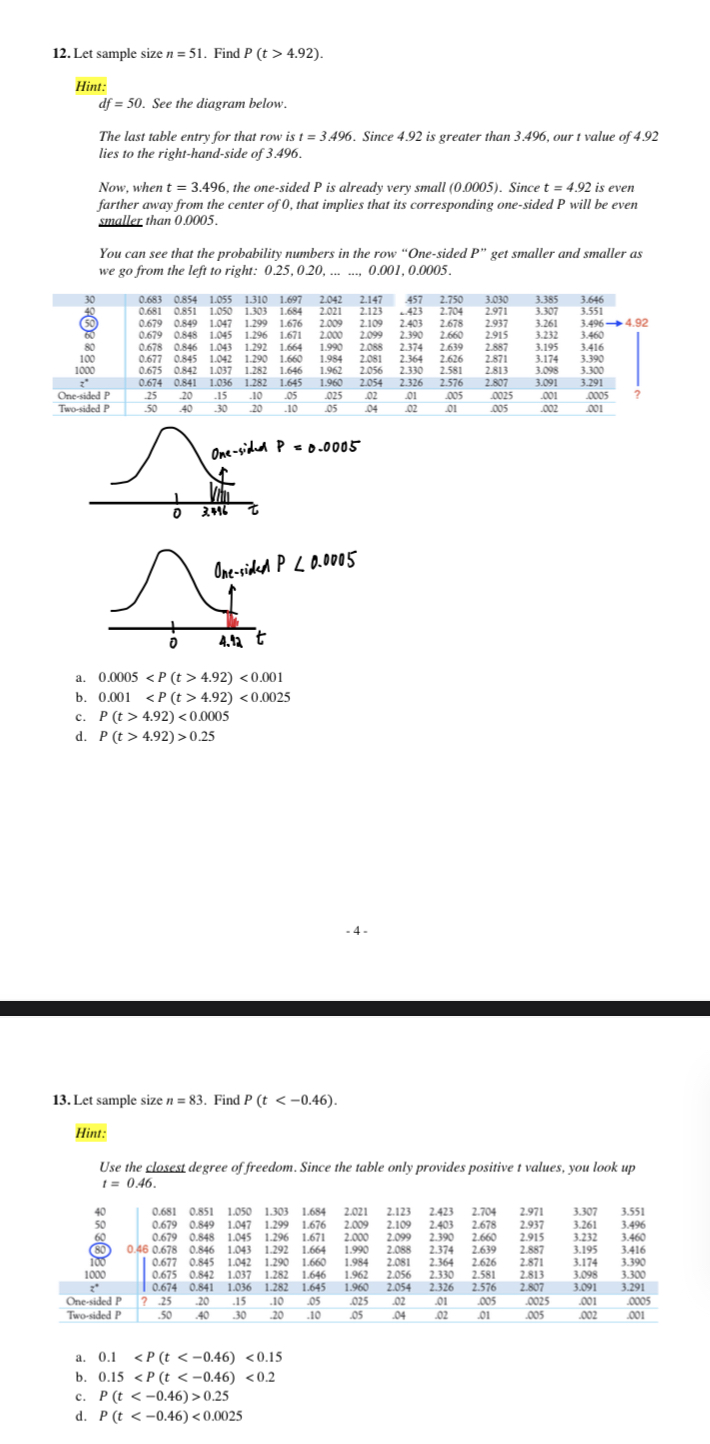
19. Let u = 20. A sample of size 10 provided a sample mean x = 18 and a sample standard deviation s = 3.2 . Find P (x > 18). Hint: Notice the #18 and # 19 have the same answer. Why? How different are the two t values? Differ by a sign only! a. 0.025 18) 18) 18) 18) 25). a. P (x > 25) 25) 25) 25) 25) above. Let's assume that as researchers, we consider a probability smaller than 5% small. Since P (x > 25) is than 5%, it is _ to have obtained such a sample mean. In other words, given that the population mean is 19, it is highly unlikely that a sample mean this far from the population mean would occur by pure chance alone. To put it in another way, the occurrence of this sample mean of 25 cast doubt on the validity of the assumption of 19. a. larger, not surprising, does not b. smaller, surprising, does c. larger, surprising, does d. smaller, not surprising, does not - 7 - 23. Let u = 78. A sample of size 26 provided a sample mean x = 77.8 and a sample standard deviation s = 2. Find P (x 22). a. 0.025 22) 22) 22) 22) 4.92). Hint: df = 50. See the diagram below. The last table entry for that row is t = 3496. Since 4.92 is greater than 3.496, our t value of 4.92 lies to the right-hand-side of 3.496. Now, when t = 3.496, the one-sided P is already very small (0.0005). Since t = 4.92 is even farther away from the center of 0, that implies that its corresponding one-sided P will be even smaller than 0.0005. You can see that the probability numbers in the row "One-sided P" get smaller and smaller as we go from the left to right: 0.25, 0.20, ... ..., 0.001, 0.0005. 30 0.683 0.854 1.055 1.310 1.697 2.042 2.147 457 2.750 3.030 3.385 3.646 0.681 0.851 1 1.050 1.303 1.684 2.021 2.123 -423 2.704 2.971 3.307 3.551 0.679 0.849 1.047 1.676 2.009 2.109 2.403 2.678 2.937 3.261 3.496- 4.92 0.679 0.848 1.045 1.296 1.671 2.000 2.099 2.390 2.660 2.915 3.232 3.460 0.678 6 1.043 1.292 1.664 1.990 2.068 2.374 2.639 2.887 3.195 3.416 100 0.677 0.845 1.042 1.290 1.660 1.984 2081 2.364 2.626 2.871 3.174 3.390 1000 0.675 0.842 1.037 1.282 1.646 1.962 2.056 2.330 2.581 2.813 3.098 3.300 0.674 0.841 1.036 1.282 1.645 1.960 2054 2.326 2.576 2.807 3.091 3.291 One-sided P -25 20 -15 -10 _05 025 02 01 005 0025 .001 0005 Two-sided P 50 40 30 20 -10 05 04 02 01 005 .002 001 One-sided P = 0- 0005 3.414 One-sided P 2 0. 0005 4.13 a. 0.0005 4.92) 4.92) 4.92) 4.92) > 0.25 - 4. 13. Let sample size n = 83. Find P (t 0.25 d. P (t 18 c. Ho : H = 18 H. : H # 18 d. Ho : * = 18 H. : X 2.80). a. 0.0005 2.80) 2.80) 2.80) 2.80) 2.80) 2.80) 2.80) 2.80) 2.80). That is, find the sum of the two tails. a. 0.001 3.33). That is, the tail areas corresponding to 3.33 and - 3.33 are the same. Therefore you can just look up t = 3.33 in Table C. a. 0.0005