- please answer the last part and check if they are right .
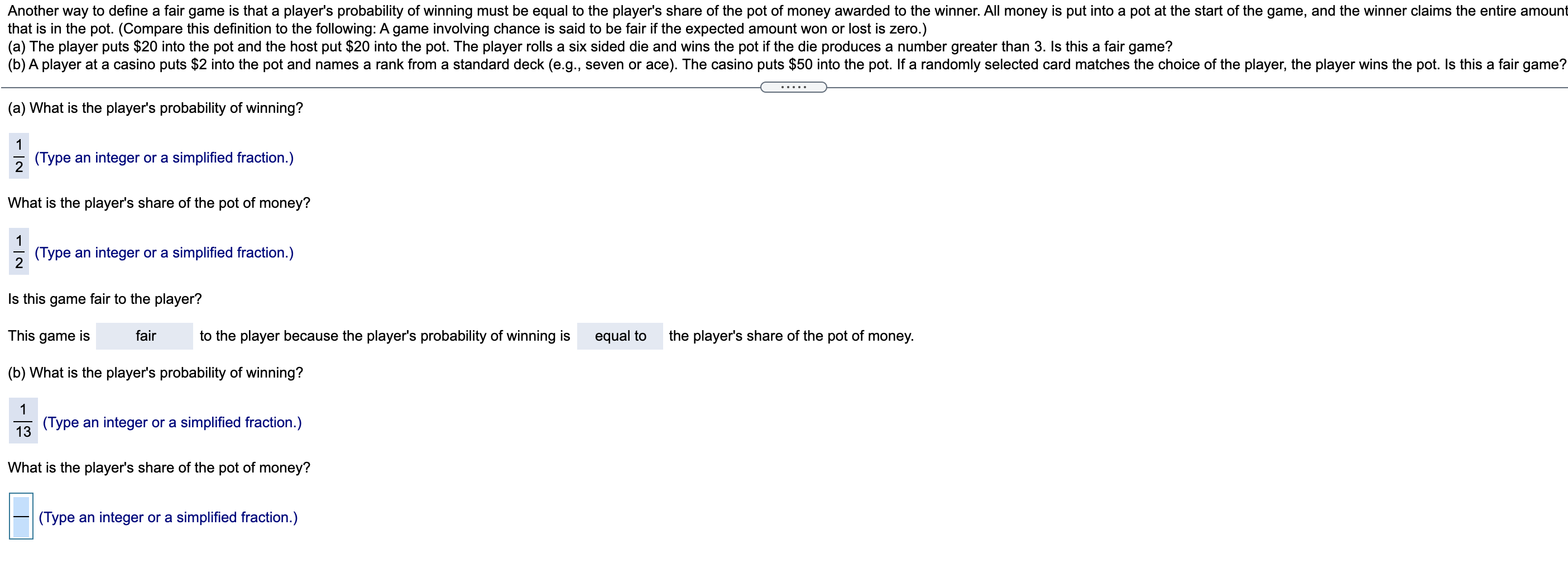
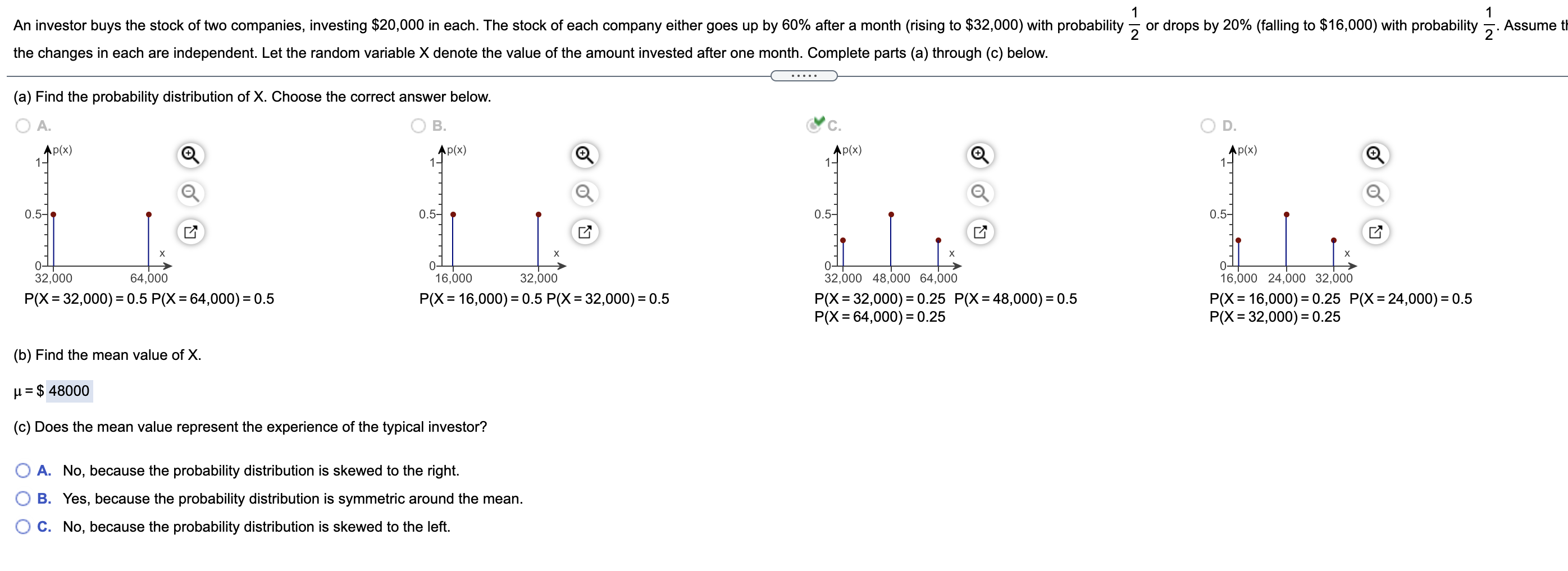
Another way to define a fair game is that a player's probability of winning must be equal to the player's share of the pot of money awarded to the winner. All money is put into a pot at the start of the game, and the winner claims the entire amount that is in the pot. (Compare this definition to the following: A game involving chance is said to be fair if the expected amount won or lost is zero.) (a) The player puts $20 into the pot and the host put $20 into the pot. The player rolls a six sided die and wins the pot if the die produces a number greater than 3. Is this a fair game? (b) A player at a casino puts $2 into the pot and names a rank from a standard deck (e.g., seven or ace). The casino puts $50 into the pot. If a randomly selected card matches the choice of the player, the player wins the pot. Is this a fair game (a) What is the player's probability of winning? N/ - (Type an integer or a simplified fraction.) What is the player's share of the pot of money? N/ - (Type an integer or a simplified fraction.) Is this game fair to the player? This game is fair to the player because the player's probability of winning is equal to the player's share of the pot of money. (b) What is the player's probability of winning? 1 13 (Type an integer or a simplified fraction.) What is the player's share of the pot of money? Type an integer or a simplified fraction.)Given that the random variable Y has mean u = 150 and SD o = 40, find the mean and SD of each of the following random variables that are defined from Y. (a) 4Y + 30 (b) 2Y Y - +0.25 (d) 10 - Y . . . . . (a) H = 630 , 6 = 160 (Simplify your answers.) (b) H= 300 , 6= (Simplify your answers.)1 1 An investor buys the stock of two companies. investing $20,000 in each. The stock of each company either goes up by 60% alter a month (rising to $32,000) with probability 5 or drops by 20% (falling to $16,000) with probability 5. Assume tl the changes in each are independent. Let the random variable X denote the value of the amount invested after one month. Complete parts (a) through (c) below. (a) Find the probability distribution of X. Choose the correct answer below. A. B. 1 P(X) Q 1 W) Q 05 0.5 [4' I3 x x o 0 32.000 64.000 16.000 32.000 P(X = 32,000) = 0.5 P(X = 64,000) = 0.5 P(X =16,000)= 0.5 P(X = 32,000) = 0.5 (b) Find the mean value of X. p = $ 48000 (0) Does the mean value represent the experience of the typical investor? O A. No. because the probability distribution is skewed to the right. 0 B. Yes, because the probability distribution is symmetric around the mean. 0 C. No, because the probability distribution is skewed to the left. '03 0.5 [1" x 0 32.000 48.000 64.000 P(X= 32,000) = 0.25 P(X = 48,000) = 0.5 P(X = 64,000) = 0.25 D. 1 pm Q Q 0.5 D" x 0 16.000 24.000 32.000 P(X =16.000)= 0.25 P(X = 24,000) = 0.5 P(X = 32,000) = 0.25 The maintenance staff of a large office building regularly replaces fluorescent ceiling lights that have gone out. During a visit to a typical floor, the staff may have to replace several lights. The manager of this staff has given the followi probabilities to the number of lights (identified by the random variable Y) that need to be replaced on a floor. Use the table to complete parts (a) through (e) below. Y 0 2 3 4 P(Y = y) 0.20 0.10 0.15 0.25 0.30 . . . . . (a) How many lights should the manager expect to replace on a floor? 2.35 lights (Round to two decimal places as needed.) (b) What is the standard deviation of the number of lights on a floor that are replaced? 1.49 lights (Round to two decimal places as needed.) (c) If a crew takes five lights to a floor, how many should it expect to have left after replacing those that are out? lights (Round to two decimal places as needed.)The government of country B pegged the value of their currency, called pesos, to the currency of government A, called dollars, at 9 pesos per dollar. Because interest rates in country B were higher than those in the country A, many investors (including banks) bought bonds in country B to eam higher returns than were available in the country A. The benets of the higher interest rates, however, masked the possibility that the peso would be allowed to float and lose substantial value compared to the dollan Suppose you are an investor and believe that the probability of the exchange rate for the next year remains at 9 pesos per dollar is 0.8, but that the rate could soar to 18 per dollar with probability 02. Complete parts (a) through (c) below. (a) Suppose you are a resident of country A. Consider two investments: Deposit $5,000 today in a savings account in countryA that pays 7% annual interest or deposit $5,000 in an account in country B that pays 13% interest, The latter requires converting the dollars into pesos at the current rate of 9 pesos/dollar and then, after a year. converting the pesos back into dollars at whatever rate then applies. Which choice has the higher expected value in one year? What is the expected value of the investment if you invest in a savings account in country A? $ (Type an integer or a decimal.) An office machine costs $10,000 to replace unless a mysterious, hard-to-find problem can be found and fixed. Repair calls from any service technician cost $500 each, and $2,000 is available to get this machine fixed. A repair technician has a 26% chance of fixing it. Complete parts (a) through (c) below. (a) Create a probability model for the number of visits needed to fix the machine or exhaust the budget of $2,000. (That is, there can be at most four visits.) p(X = 1) = 0.26 p(X =2) = 0.1924 p(X =3) = 1.1424 p(X = 4) = 1.1054 = (szx)d (Round to four decimal places as needed.)