please assist with solutions

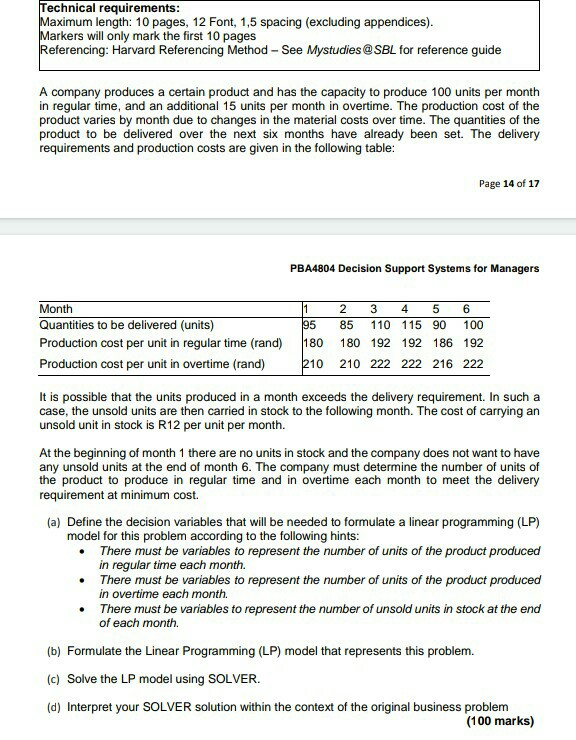
Technical requirements: Maximum length: 10 pages, 12 Font, 1,5 spacing (excluding appendices). Markers will only mark the first 10 pages Referencing: Harvard Referencing Method - See Mystudies @ SBL for reference guide A company produces a certain product and has the capacity to produce 100 units per month in regular time, and an additional 15 units per month in overtime. The production cost of the product varies by month due to changes in the material costs over time. The quantities of the product to be delivered over the next six months have already been set. The delivery requirements and production costs are given in the following table: Page 14 of 17 PBA4804 Decision Support Systems for Managers Month Quantities to be delivered (units) Production cost per unit in regular time (rand) Production cost per unit in overtime (rand) 1 95 180 2 3 4 5 6 85 110 115 90 100 180 192 192 186 192 210 222 222 216 222 210 It is possible that the units produced in a month exceeds the delivery requirement. In such a case, the unsold units are then carried in stock to the following month. The cost of carrying an unsold unit in stock is R12 per unit per month. At the beginning of month 1 there are no units in stock and the company does not want to have any unsold units at the end of month 6. The company must determine the number of units of the product to produce in regular time and in overtime each month to meet the delivery requirement at minimum cost. (a) Define the decision variables that will be needed to formulate a linear programming (LP) model for this problem according to the following hints: There must be variables to represent the number of units of the product produced in regular time each month. There must be variables to represent the number of units of the product produced in overtime each month. There must be variables to represent the number of unsold units in stock at the end of each month. (b) Formulate the Linear Programming (LP) model that represents this problem. (c) Solve the LP model using SOLVER. (d) Interpret your SOLVER solution within the context of the original business problem (100 marks) Technical requirements: Maximum length: 10 pages, 12 Font, 1,5 spacing (excluding appendices). Markers will only mark the first 10 pages Referencing: Harvard Referencing Method - See Mystudies @ SBL for reference guide A company produces a certain product and has the capacity to produce 100 units per month in regular time, and an additional 15 units per month in overtime. The production cost of the product varies by month due to changes in the material costs over time. The quantities of the product to be delivered over the next six months have already been set. The delivery requirements and production costs are given in the following table: Page 14 of 17 PBA4804 Decision Support Systems for Managers Month Quantities to be delivered (units) Production cost per unit in regular time (rand) Production cost per unit in overtime (rand) 1 95 180 2 3 4 5 6 85 110 115 90 100 180 192 192 186 192 210 222 222 216 222 210 It is possible that the units produced in a month exceeds the delivery requirement. In such a case, the unsold units are then carried in stock to the following month. The cost of carrying an unsold unit in stock is R12 per unit per month. At the beginning of month 1 there are no units in stock and the company does not want to have any unsold units at the end of month 6. The company must determine the number of units of the product to produce in regular time and in overtime each month to meet the delivery requirement at minimum cost. (a) Define the decision variables that will be needed to formulate a linear programming (LP) model for this problem according to the following hints: There must be variables to represent the number of units of the product produced in regular time each month. There must be variables to represent the number of units of the product produced in overtime each month. There must be variables to represent the number of unsold units in stock at the end of each month. (b) Formulate the Linear Programming (LP) model that represents this problem. (c) Solve the LP model using SOLVER. (d) Interpret your SOLVER solution within the context of the original business problem (100 marks)