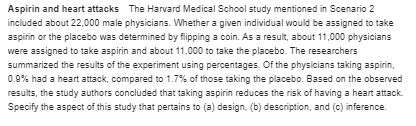Please assist with step by step explanation:-
Which questions is incomplete jQuery22409170933673888326_1623144393432
\fGender gap in politics? In the United States, is there a gender gap in political beliefs? That is, do women and men tend to differ in their political thinking and voting behavior? The table taken from the 2012 GSS relates gender and political party identification. Subjects indicated whether they identified more strongly with the Democratic or Republican party or as Independents. Political Party Identification Gender Democrat Independent Republican Total Female 421 398 244 1063 Male 278 367 198 843 Source: Data from CSM, UC Berkeley a. Identify the response variable and the explanatory variable. b. Construct a table that shows the conditional distributions of the response variable. Interpret. C. Give a hypothetical example of population conditional distributions for which these variables would be independent. d. Sketch bar graphs to portray the distributions in part b and in part c.Beliefs of college freshmen Every year, a large-scale poll of college freshmen conducted by the Higher Education Research Institute at UCLA asks their opinions about a variety of issues. In 2004, although women were more likely to rate their time management skills as "above average, they were also twice as likely as men to indicate that they frequently feel overwhelmed by all they have to do (36.4% versus 16.3%). a. If results for the population of college freshmen were similar to these, would gender and feelings of being overwhelmed be independent or dependent? b. Give an example of hypothetical population percentages for which these variables would be independent.Williams College admission Data from 2013 posted on the Williams College website shows that of all 3,195 males applying. 18.2% were admitted, and of all 3,858 females applying. 16.9% were admitted. Let X denote gender of applicant and Y denote whether admitted. a. Which conditional distributions do these percentages refer to, those of Y at given categories of X, or those of X at given categories of Y? Set up a table showing the two conditional distributions. b. Are X and Y independent or dependent? Explain. (Hint: These percentages refer to the population of all applicants in 2013.)Happiness and gender The contingency table shown relates happiness and gender for the 2012 GSS. Happiness Gender Not Too Happy Pretty Happy Very Happy Total Female 154 592 336 1082 Male 123 502 257 882 Source: Data from CSM, UC Berkeley. a. Identify the response variable and the explanatory variable. b. Construct a table or graph showing the conditional distributions. Interpret. C. Give an example of population conditional distributions (i.e., proportions or percentages) that would seem to be consistent with this sample and for which happiness and gender would be independent.What is independent of happiness? Which one of the following variables would you think most likely to be independent of happiness: belief in an afterlife, family income, quality of health, region of the country in which you live, satisfaction with job? Explain the basis of your reasoning.Sample evidence about independence Refer to the exercise 1. Go to the GSS Web site and construct a table relating happiness (HAPPY) to the variable you chose (AFTERLIF, FINRELA. HEALTH, REGION, or JOBSAT). Inspect the conditional distributions and indicate whether independence seems plausible, with the sample conditional distributions all being quite similar. Exercise 1 What is independent of happiness? Which one of the following variables would you think most likely to be independent of happiness: belief in an afterlife, family income, quality of health, region of the country in which you live, satisfaction with job? Explain the basis of your reasoning.Life after death and gender In the 2012 GSS, 605 of 790 males and 822 of 977 females indicated a belief in life after death. (Source: Data from CSM. UC Berkeley.) a. Construct a 2 x 2 contingency table relating gender of respondent (SEX, categories male and female) as the rows to belief about life after death (POSTLIFE, categories yes and no) as the columns. b. Find the four expected cell counts when assuming independence. Compare them to the observed cell counts, identifying cells having more observations than expected. c. For this data, X" = 18.0. Verify this value by plugging into the formula for X" and computing the Sum.Happiness and gender For the 2 x 3 table on gender and happiness in Exercise 11.4 (shown below), software tells us that X" = 1.04 and the P-value = 0.59. Happiness Gender Not Pretty Very Female 154 592 336 Male 123 502 257 3. State the null and alternative hypothesis, in context, to which these results apply. b. Interpret the P-value. Reference: Exercise 11.4 11.14 Smoking and alcohol Refer to the previous exercise. A similar table relates cigarette use to alcohol use. The MINITAB output for the chi-squared test follows. a. True or false: If we use cigarette use as the column variable and alcohol use as the row variable, then we will get different values for the chi-squared statistic and the P-value shown in the output. b. Explain what value you would get for the z statistic and P-value if you conducted a significance test of Ho: pi = p2 against He: p, # pz, where pi is the pop- ulation proportion of non-cigarette users who have drunk alcohol and pz is the population proportion of cigarette users who have drunk alcohol. Dayton student survey Row: cigarette Columns: alcohol no yes no 281 500 yes 46 1449 Pearson Chi-Square - 451 . 404, DF = 1, P-value = 0. 000What gives P-value = 0.05? How large a X2 test statistic value provides a P-value of 0.05 for testing independence for the following table dimensions? a. 2x 2 b. 2x3 C. 2 x 5 d. 5x5 e. 3x9Marital happiness and income In Exercise 11.5 when you used the GSS to download a 3 x 3 table for family income and marital happiness in 2012, you should have obtained results similar to the following table. Marital Happiness Income Not Pretty Very Above 62 139 Average 125 283 Below 6 69 115 a. State the null and alternative hypotheses for the test. b. What is the number of degrees of freedom for the chi-squared test? C. The chi-squared statistic for the table equals X" = 4.58. (@) What value do you expect for X if the null hypothesis were true? (ii) How many standard deviations is 4.58 from this expected V2 x df). (mi) Is X