Please, carefully read the request's instructions: -
Kindly, DO NOT answer this question if you have either already answered it before or are unable to answer ALL parts of it.
Respectfully, please only answer if you can SOLVE ALL PARTS - INCLUDING OPTIONAL PARTS (if any). This is all ONE question with multiple parts/steps: (a) - (e). Please answer ALL PARTS (INCLUDING OPTIONAL PARTS, IF ANY). Kindly guide me through the process. Please be concise, legible and thorough.
.
.
.
.
PLEASE MAKE SURE YOU READ THE INSTRUCTIONS! Answer parts a - e. NOT JUST A SINGLE PART. PLEASE. IF NEEDED, SKIP ANSWERING PART A AND ANSWER PARTS (B) - (E).
.
.
.
.
.
.
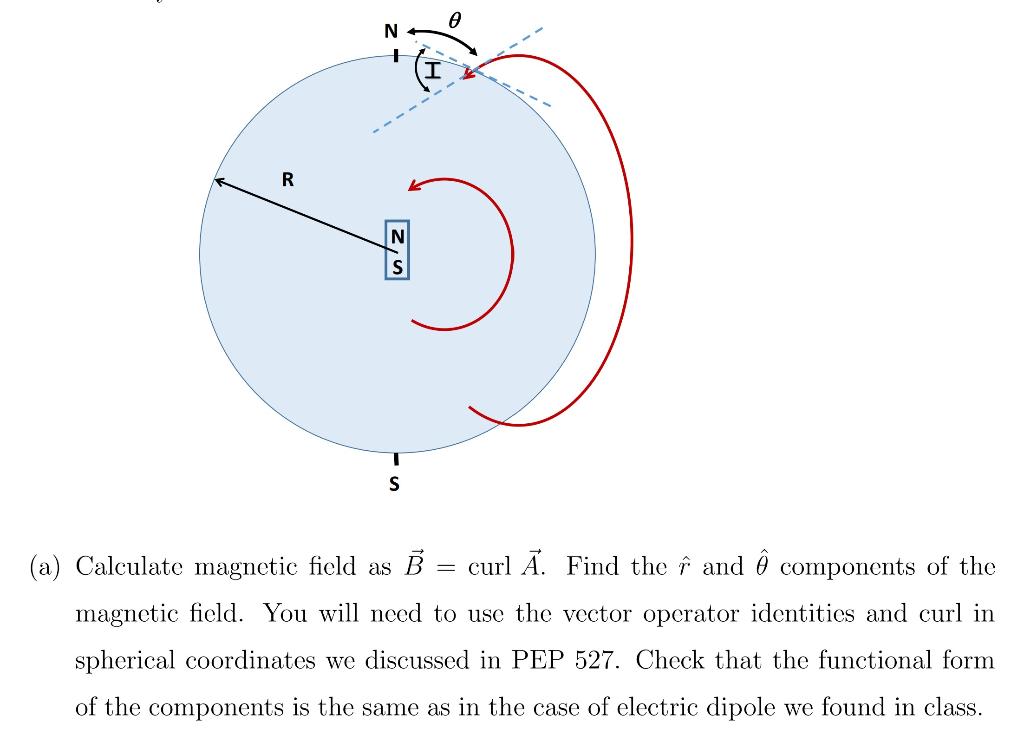
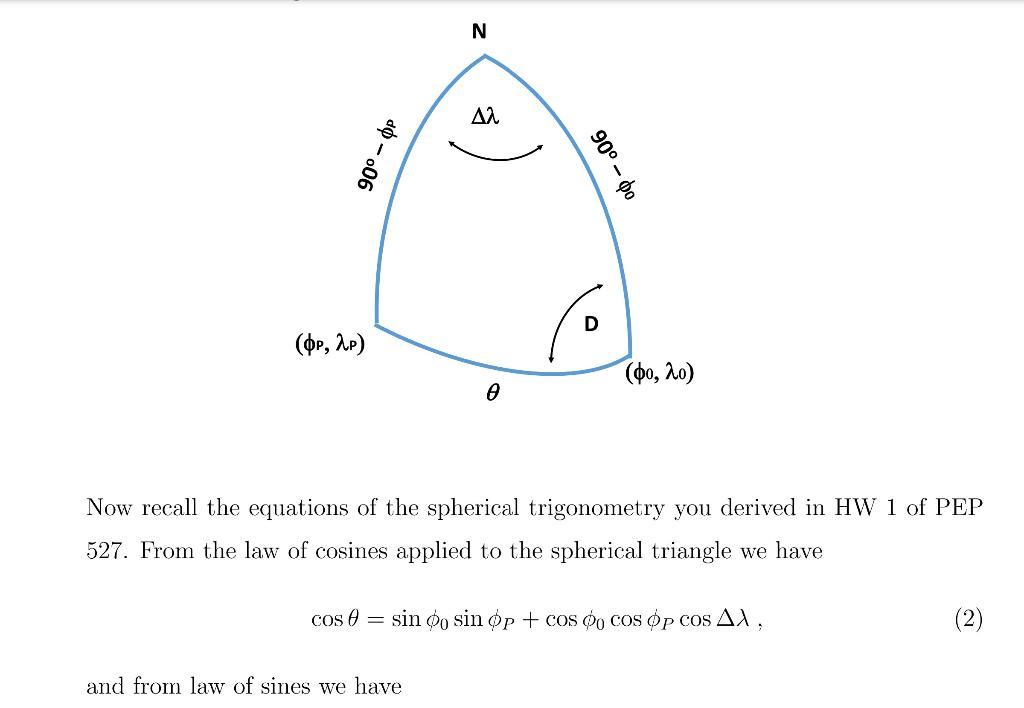
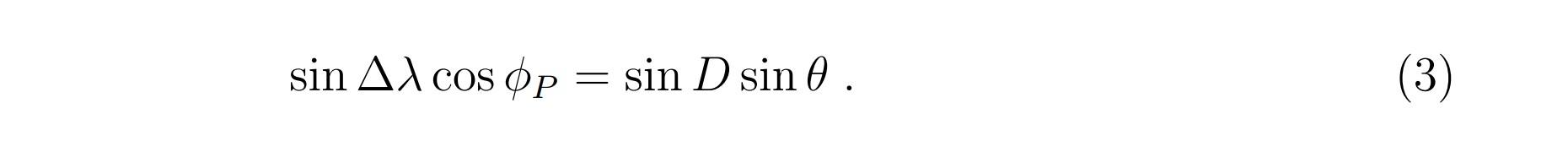
Problem 6. (Paleomagnetism.] Continents move due to the plate tectonics, and geologists have many ways to deter- mine the position of the part of the continental crust at the time of its formation. One method is based on the measurement of magnetization of the crust. As magnetic crustal minerals cooled below Currie temperature, they were magnetized in the direc- tion of the local Earth's magnetic field. The calculations are typically done in the dipole approrimation of Earth's magnetic field. Stationary dipole magnetic field can be derived from the magnetic vector potential A defined using the dipole moment vector as A = Ho x i 47 r3 Dipole moment is assumed to be positioned in the center of the Earth, shown as a small bar magnet in the image below. Symmetry dictates the use of spherical coordinate system. e N R IN S T S (a) Calculate magnetic field as B curl A. Find the f and components of the magnetic field. You will need to use the vector operator identities and curl in spherical coordinates we discussed in PEP 527. Check that the functional form of the components is the same as in the case of electric dipole we found in class. = (b) Consider the magnetic field at the surface of the Earth at radius r = R, and at the polar coordinate 0. The inclination of the magnetic field relative to the horizontal direction is I. Show that 2 tan 1 (1) tan Consider two points on the Earth: latitudes and longitudes (0o, lo) are the coordinates of the observer, and (op, \p) are the coordinates of the magnetic pole. The angle along the meridian lines between the north pole and the two points are 90 - oo and 90 P ; the angle between the two meridian lines is 8) = \p - o. Angle D is the azimuth of the magnetic north pole from the position of observation. Angle @ from part (b) is also shown in the figure. N A2 do -06 o06 (op, 2p) (, ) Now recall the equations of the spherical trigonometry you derived in HW 1 of PEP 527. From the law of cosines applied to the spherical triangle we have cos 6 = sin oo sin op + cos o cos op Cos AX, (2) and from law of sines we have sin Al cos op = sin D sin 8. (3) (c) Using the same method as in rotation matrices applied to the spherical triangle in the figure derive equations (2) and (3). . (d) From the known geographical coordinates of the North Magnetic Pole and of Hoboken, find the numerical values of angles I and D (in degrees) that magnetic field makes in Hoboken. Practical use of the above problems is opposite of what you've done in parts (b) and (d). We can measure in situ the inclination of the rock magnetization I, and the angle D magnetization makes with geographic north. From measured I and D and known coordinates of the sample location, using equations (1), (2) and (3), we can determine the current coordinates of the magnetic pole (op, !p) at the time of the formation of the sample (sometimes called virtual magnetic pole). (e) The measurements of early Cratecous limestone in Italian Apennines at geograph- ical coordinates oo 42.9 north, and lo = 12.6 east yield the mean values of I 38 and D = 313 [1]. Find the present geographical coordinates of the location of (op, \p) of what was the magnetic pole at the time of the formation of the sample. Where is that place located on Earth? = Note that magnetic pole is usually close to the geographic pole, though its exact co- ordinates change with time. When samples of the same geological age are measured on different continents, one can deduce their relative positions and orientations. By repeating the same measurements on the layers of different age ('magnetostratigra- phy'), we can deduce the motion of the continents through geological ages. We can similarly find the records of geomagnetic reversal, when consecutive layers have oppo- site directions of magnetization. It is worth mentioning that this method is statistical in nature, i.e. one typically makes many magnetization measurements in the same geological layer. [1] By geological convention angle D is measured from north in the clockwise direction - if you want to use the counterclockwise angle like we did in the above figure, use D = 360 - 3139 = 47. Problem 6. (Paleomagnetism.] Continents move due to the plate tectonics, and geologists have many ways to deter- mine the position of the part of the continental crust at the time of its formation. One method is based on the measurement of magnetization of the crust. As magnetic crustal minerals cooled below Currie temperature, they were magnetized in the direc- tion of the local Earth's magnetic field. The calculations are typically done in the dipole approrimation of Earth's magnetic field. Stationary dipole magnetic field can be derived from the magnetic vector potential A defined using the dipole moment vector as A = Ho x i 47 r3 Dipole moment is assumed to be positioned in the center of the Earth, shown as a small bar magnet in the image below. Symmetry dictates the use of spherical coordinate system. e N R IN S T S (a) Calculate magnetic field as B curl A. Find the f and components of the magnetic field. You will need to use the vector operator identities and curl in spherical coordinates we discussed in PEP 527. Check that the functional form of the components is the same as in the case of electric dipole we found in class. = (b) Consider the magnetic field at the surface of the Earth at radius r = R, and at the polar coordinate 0. The inclination of the magnetic field relative to the horizontal direction is I. Show that 2 tan 1 (1) tan Consider two points on the Earth: latitudes and longitudes (0o, lo) are the coordinates of the observer, and (op, \p) are the coordinates of the magnetic pole. The angle along the meridian lines between the north pole and the two points are 90 - oo and 90 P ; the angle between the two meridian lines is 8) = \p - o. Angle D is the azimuth of the magnetic north pole from the position of observation. Angle @ from part (b) is also shown in the figure. N A2 do -06 o06 (op, 2p) (, ) Now recall the equations of the spherical trigonometry you derived in HW 1 of PEP 527. From the law of cosines applied to the spherical triangle we have cos 6 = sin oo sin op + cos o cos op Cos AX, (2) and from law of sines we have sin Al cos op = sin D sin 8. (3) (c) Using the same method as in rotation matrices applied to the spherical triangle in the figure derive equations (2) and (3). . (d) From the known geographical coordinates of the North Magnetic Pole and of Hoboken, find the numerical values of angles I and D (in degrees) that magnetic field makes in Hoboken. Practical use of the above problems is opposite of what you've done in parts (b) and (d). We can measure in situ the inclination of the rock magnetization I, and the angle D magnetization makes with geographic north. From measured I and D and known coordinates of the sample location, using equations (1), (2) and (3), we can determine the current coordinates of the magnetic pole (op, !p) at the time of the formation of the sample (sometimes called virtual magnetic pole). (e) The measurements of early Cratecous limestone in Italian Apennines at geograph- ical coordinates oo 42.9 north, and lo = 12.6 east yield the mean values of I 38 and D = 313 [1]. Find the present geographical coordinates of the location of (op, \p) of what was the magnetic pole at the time of the formation of the sample. Where is that place located on Earth? = Note that magnetic pole is usually close to the geographic pole, though its exact co- ordinates change with time. When samples of the same geological age are measured on different continents, one can deduce their relative positions and orientations. By repeating the same measurements on the layers of different age ('magnetostratigra- phy'), we can deduce the motion of the continents through geological ages. We can similarly find the records of geomagnetic reversal, when consecutive layers have oppo- site directions of magnetization. It is worth mentioning that this method is statistical in nature, i.e. one typically makes many magnetization measurements in the same geological layer. [1] By geological convention angle D is measured from north in the clockwise direction - if you want to use the counterclockwise angle like we did in the above figure, use D = 360 - 3139 = 47
