Please do number 25 P1. The answer is at the bottom. I just need the work. An example of something similar to 25 is:

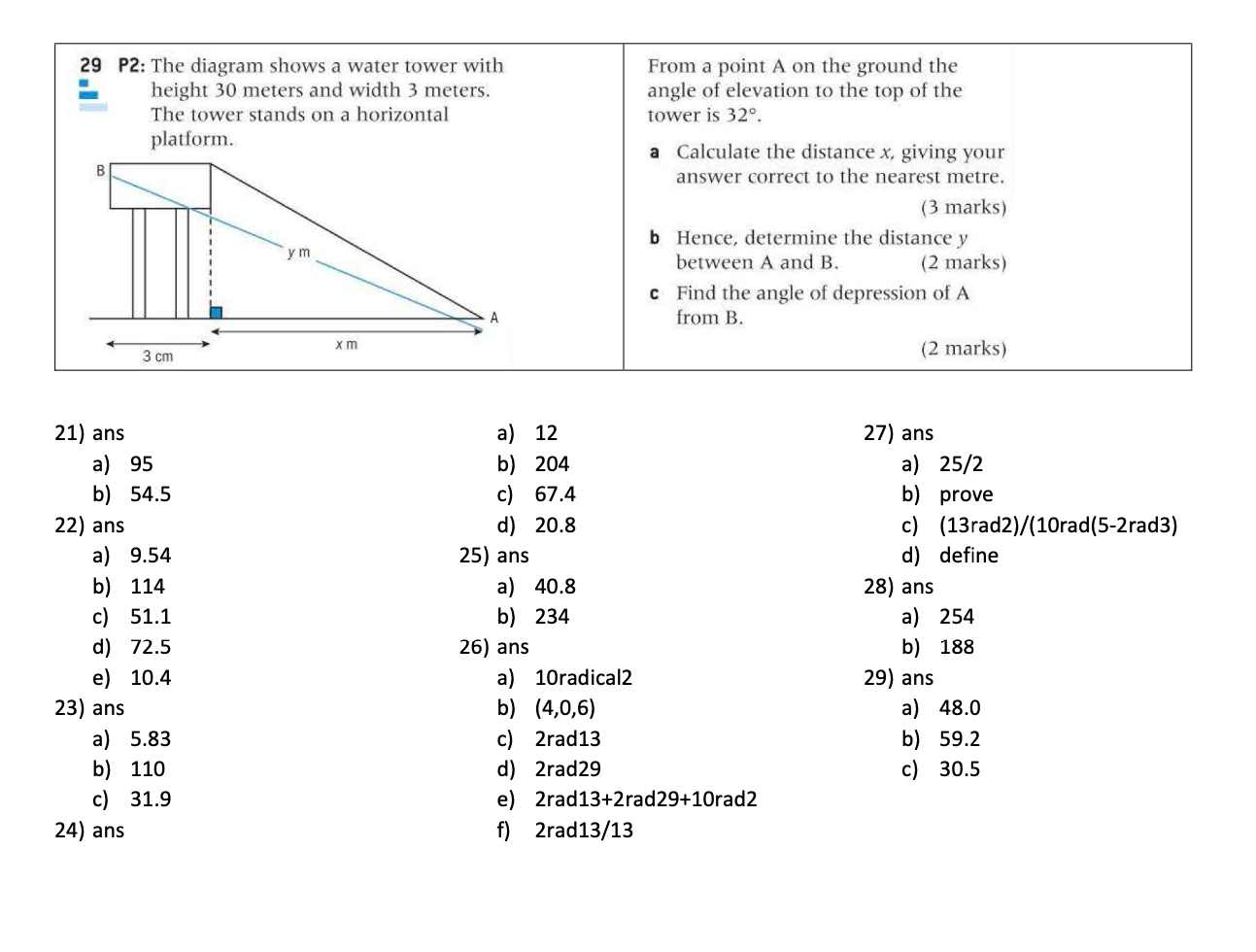
29 ?2: The diagram shows a water tower with '- height 30 meters and width 3 meters. The tower stands on a horizontal platform. From a point A on the ground the angle of elevation to the top of the tower is 32. a Calculate the distance x. giving your answer correct to the nearest metre. (3 marks) Hence, determine the distance y between A and B. (2 marks) Find the angle of depression of A from B. (2 marks) a) 12 27) ans b) 204 a} 25/2 c) 67.4 b) prove d) 20.8 c) (13rad2)/(10rad(52rad3) 25) ans cl) define a) 40.3 23} ans b) 234 a) 254 26) ans b) 188 a) 10radica|2 29} ans b) (4,0,6) 3} 48.0 c) 2rad13 b) 59.2 d) 2rad29 c) 30.5 e} 2rad13+2rad29+10rad2 f) 2rad13/13 24 92: Considera trapezium ABCD with AB- _. CD and BC parallel to AD. Given thatAB = 13cm. BC=12 cm. andAD= 22 cm. a show that the trapezium has height 13 centimetres. {3 marks} I: Hence. End the area of the trapezium. (2 marks) I: Find the size of the angie D. (3 marks) d Calculate the length 01 the diagonal AC. (3 marks] 26 P2: The diagram shows a cuboid ABCDEFGH. ' The vertex F' is located at the origin of a plane and the vertex C has coordinates (8, IO, 6). The faces of the cuboid are parallel to the coordinate planes. 25 P1: A ship leaves a port located at point A on a bearing of 030. It sails a distance of 20 km to a point B where it changes direction to a beating 0175\". Then it sails 25 km to reach a port located at a point C. 3 Find the distance between A and C. (4 marks} in Find the bearing of the point C with respect to A. (3 marks) Show that the length of the diagonal of the cuboid is 105 cm. (2 marks} Determine the coordinates of the midpoint M of the segment AD. (2 marks} Find the distance between the points F and M. (2 marks} Find the perimeter of the triangle CFM, giving your ansWer exactly. {3 marks} Show that cosine of the angle AMP is e ual to E. q 10 (3 marks) 2? P1: The diagram below shows a ' quadrilateral ABCD such that "' AB=10 cm AD =5 cm BC: 13cm BCD= 45\" and BAD: 30\". c D I 13 cm A 10 cm 3 Find the exact area of the triangle ABD. (2 marks) Show that B0 = 5J5 - 2J5. (4 marks) Find the exact value of sinCB. (3 marks) Hence, explain why there are two possibleAvalues for the size of the angle CBD, stating the relationship between the two possible values. [2 marks) 28 P2: The gure shows a container in the ' shape of a circular cylinder topped by a hemisphere. The radii ol both cylinder and hemisphere is 3 centimetres and the height of the cylinder is 7 centimetres. 70m Calculate: I: the volume of the container (4 marks) the total surface area of the container. (3 marks) Answer/Explanation Markscheme finding ABC = 110 (= 1.92 radians) (A1) evidence of choosing cosine rule (Mi) e.g. AC2 = AB2 + BC2-2(AB) (BC) cos ABC correct substitution A1 e.g. AC2 = 252 + 402-2(25) (40) cos 110 AC = 53.9 (km) A1 a.A ship leaves port A on a bearing of 0300 . It sails a distance of 25 km to point B. At B, the ship changes direction to a bearing of 100 . It sails a distance of 40 km to reach point C. This information is Shown in the diagram below. C diagram not to scale A second ship leaves port A and sails directly to C. Find the distance the second ship will travel. [4] a. Find the bearing of the course taken by the second ship. [3] METHOD 1 correct substitution into the sine rule A1 e.g. sin BAC - sin 110 40 53.9 A1 BAC = 44.2 bearing = 074 A1 N1 METHOD 2 correct substitution into the cosine rule Ai e.g. cos BAC = 40'-252-53.92 -2(25) (53.9) A1 BAC = 44.3 bearing = 074 A1 N1 [3 marks] b