Please explain step by step,

also, could you write some basic code of Mathlab that it will help me to code the solution?

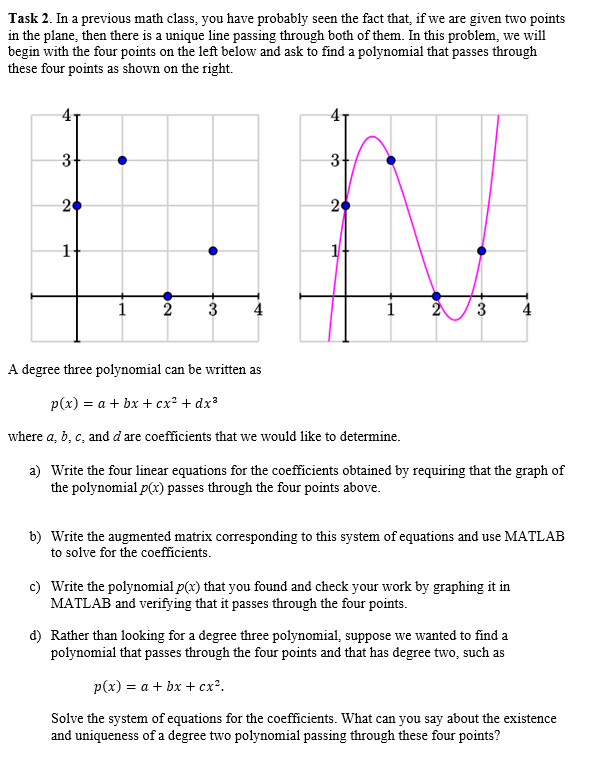
Purpose: The purpose of this lab is for you to learn how to use a computer to solve problems dealing with systems of equations. In future classes and when you are working in industry, linear algebra will be one of the most important areas of math you use to solve complex problems, that are only solvable with the use of a computer. Skills: Translating a problem into a set of equations that can be solved by a computer. Using MATLAB to solve a system of linear equations. Explaining what the reduced row echelon form of a matrix means for a particular application problem. Knowledge Interpreting the reduced row echelon form of a matrix to determine the existence and uniqueness of a solution. Writing the parametric form of the solution for an infinite number of solutions using a parameter, like t, instead of a variable, like z. Preliminaries Four things that need to be done before starting the lab. Complete the MATLAB Onramp Tutorial. The tutorial includes basic information on how to use MATLAB. Complete the worksheets from Canvas and read through Sections 1.1, 1.2, and 1.3 of the textbook. Create a directory on Microsoft's OneDrive, or some other cloud-based storage location, where you can put files that you can access from South's network and your home computer. Try accessing MATLAB from your home computer. Don't wait until an hour before the assignment is due to try it. Submission format: Upload a pdf of your typed report. What to turn in for each task. The problem description. You can copy the description from this document. Explain the principle you are using to write the equations. Write the set of equations used to describe the system. (Use the equation editor in Word, or something similar. Ask for help if you don't know how to use it.) Rewrite the equations into the form you will use to create an augmented matrix. Explain what method you are going to use to solve the system of equations. For this lab, you will be using an augmented matrix and the rref command in MATLAB, which uses the Gauss Jordan elimination method. For other labs, you may use different methods. Write the augmented matrix. Write the MATLAB commands used to solve the problem. Paste in a copy of the output from MATLAB. Explain how you determined if the system is consistent or inconsistent. For a consistent system, explain how you determined if the system had a unique solution or an infinite number of solutions. Write the solution to the system of equations. For any tasks that ask specific questions, be sure to answer the questions. Explain what the solution means in terms of the application problem you are solving. Example: Use the reduced row echelon form (rref) command to solve a system of linear equations in MATLAB. To find the solution to the augmented matrix Ti - 2 3 A = -1 3 0 2 -5 5 9 -4 17 Create the augmented matrix in MATLAB, A = [1 -23 9-130-4;2-5 5 17]; Typing rref(A) in the command window of MATLAB will return the reduced row echelon form of the matrix. [1 0 0 1 rref(A) - 0 1 0 -1 0 0 1 2 It is up to you to interpret and state what the solution means. You do not say the answer is the matrix, instead you need to state how you know the matrix is consistent or inconsistent. Then give the solution. For this example, you could say, For the augmented matrix A, columns 1, 2 and 3 are pivot columns, so there is a unique solution. The solution is x = 1, y =-1, and = = 2. 1 Example: Let 0 -2 -41 rref(A) = 0 1 5 3 0 0 0 0 be the reduced row echelon form of an augmented matrix A. Solution The fourth column is not a pivot column, so the linear system represented by the matrix is consistent. Columns 1 and 2 are pivot columns, so x and y are basic variables. Column 3 represents a free variable. The row reduced matrix corresponds to the linear system x 2z = -4 and y + 5z = 3. Since z is a free variable, let z = t. The solution to the linear system is then (2t 4,3 5t,t). The following three tasks describe the problems you are to solve using MATLAB. Task 1. A typical problem in thermodynamics is to find the steady-state temperature distribution inside a thin plate if we know the temperature around the boundary. Let T1, T2, To be the temperatures at the six nodes inside the plate as shown below. 15 20 25 Ti T2 T3 10 30 TA T5 . 10 40 10 20 30 The temperature at a node is approximately the average of the four nearest nodes: for instance, (10 + 15 +T, +T) T1 = 4 Set up a linear system to find the temperature at these six points inside the plate. Then use MATLAB to solve the linear system. In the real world, the approximation becomes better the closer the points are together, which happens as we add more and more points into the grid. This is a situation where we would want to solve linear systems having millions of equations and millions of unknowns. Task 2. In a previous math class, you have probably seen the fact that, if we are given two points in the plane, then there is a unique line passing through both of them. In this problem, we will begin with the four points on the left below and ask to find a polynomial that passes through these four points as shown on the right. 3 3 2 2 2 1 2 3 4 4 2 3 4 A degree three polynomial can be written as p(x) = a + bx + cx + dx3 where a, b, and d are coefficients that we would like to determine. a) Write the four linear equations for the coefficients obtained by requiring that the graph of the polynomial p(x) passes through the four points above. b) Write the augmented matrix corresponding to this system of equations and use MATLAB to solve for the coefficients. c) Write the polynomial p(x) that you found and check your work by graphing it in MATLAB and verifying that it passes through the four points. d) Rather than looking for a degree three polynomial, suppose we wanted to find a polynomial that passes through the four points and that has degree two, such as p(x) = a +bx+cx Solve the system of equations for the coefficients. What can you say about the existence and uniqueness of a degree two polynomial passing through these four points? e) Rather than looking for a degree three polynomial, suppose we wanted to find a polynomial that passes through the four points and that has degree four, such as p(x) = a +bx+cx2 + dx + ex*. Solve the system of equations for the coefficients. What can you say about the existence and uniqueness of a degree four polynomial passing through these four points? f) Suppose you had 10 points and you wanted to find a polynomial passing through each of them. What should the degree of the polynomial be to guarantee that there is exactly one such polynomial? Explain your response. Task 3. The network in Figure 1 shows the traffic flow in vehicles per hour) over several one- way streets in downtown Baltimore during a typical early afternoon. Determine the general flow pattern for the network. This means to find the traffic flow on the sections of street between AB, CB, CD, and AD. 100 South St. Calvert St. Z Lombard St. B 300+ +400 4 132 Pratt St. A D 300 600 Inner Harbor 500 Figure 1 Baltimore streets. Purpose: The purpose of this lab is for you to learn how to use a computer to solve problems dealing with systems of equations. In future classes and when you are working in industry, linear algebra will be one of the most important areas of math you use to solve complex problems, that are only solvable with the use of a computer. Skills: Translating a problem into a set of equations that can be solved by a computer. Using MATLAB to solve a system of linear equations. Explaining what the reduced row echelon form of a matrix means for a particular application problem. Knowledge Interpreting the reduced row echelon form of a matrix to determine the existence and uniqueness of a solution. Writing the parametric form of the solution for an infinite number of solutions using a parameter, like t, instead of a variable, like z. Preliminaries Four things that need to be done before starting the lab. Complete the MATLAB Onramp Tutorial. The tutorial includes basic information on how to use MATLAB. Complete the worksheets from Canvas and read through Sections 1.1, 1.2, and 1.3 of the textbook. Create a directory on Microsoft's OneDrive, or some other cloud-based storage location, where you can put files that you can access from South's network and your home computer. Try accessing MATLAB from your home computer. Don't wait until an hour before the assignment is due to try it. Submission format: Upload a pdf of your typed report. What to turn in for each task. The problem description. You can copy the description from this document. Explain the principle you are using to write the equations. Write the set of equations used to describe the system. (Use the equation editor in Word, or something similar. Ask for help if you don't know how to use it.) Rewrite the equations into the form you will use to create an augmented matrix. Explain what method you are going to use to solve the system of equations. For this lab, you will be using an augmented matrix and the rref command in MATLAB, which uses the Gauss Jordan elimination method. For other labs, you may use different methods. Write the augmented matrix. Write the MATLAB commands used to solve the problem. Paste in a copy of the output from MATLAB. Explain how you determined if the system is consistent or inconsistent. For a consistent system, explain how you determined if the system had a unique solution or an infinite number of solutions. Write the solution to the system of equations. For any tasks that ask specific questions, be sure to answer the questions. Explain what the solution means in terms of the application problem you are solving. Example: Use the reduced row echelon form (rref) command to solve a system of linear equations in MATLAB. To find the solution to the augmented matrix Ti - 2 3 A = -1 3 0 2 -5 5 9 -4 17 Create the augmented matrix in MATLAB, A = [1 -23 9-130-4;2-5 5 17]; Typing rref(A) in the command window of MATLAB will return the reduced row echelon form of the matrix. [1 0 0 1 rref(A) - 0 1 0 -1 0 0 1 2 It is up to you to interpret and state what the solution means. You do not say the answer is the matrix, instead you need to state how you know the matrix is consistent or inconsistent. Then give the solution. For this example, you could say, For the augmented matrix A, columns 1, 2 and 3 are pivot columns, so there is a unique solution. The solution is x = 1, y =-1, and = = 2. 1 Example: Let 0 -2 -41 rref(A) = 0 1 5 3 0 0 0 0 be the reduced row echelon form of an augmented matrix A. Solution The fourth column is not a pivot column, so the linear system represented by the matrix is consistent. Columns 1 and 2 are pivot columns, so x and y are basic variables. Column 3 represents a free variable. The row reduced matrix corresponds to the linear system x 2z = -4 and y + 5z = 3. Since z is a free variable, let z = t. The solution to the linear system is then (2t 4,3 5t,t). The following three tasks describe the problems you are to solve using MATLAB. Task 1. A typical problem in thermodynamics is to find the steady-state temperature distribution inside a thin plate if we know the temperature around the boundary. Let T1, T2, To be the temperatures at the six nodes inside the plate as shown below. 15 20 25 Ti T2 T3 10 30 TA T5 . 10 40 10 20 30 The temperature at a node is approximately the average of the four nearest nodes: for instance, (10 + 15 +T, +T) T1 = 4 Set up a linear system to find the temperature at these six points inside the plate. Then use MATLAB to solve the linear system. In the real world, the approximation becomes better the closer the points are together, which happens as we add more and more points into the grid. This is a situation where we would want to solve linear systems having millions of equations and millions of unknowns. Task 2. In a previous math class, you have probably seen the fact that, if we are given two points in the plane, then there is a unique line passing through both of them. In this problem, we will begin with the four points on the left below and ask to find a polynomial that passes through these four points as shown on the right. 3 3 2 2 2 1 2 3 4 4 2 3 4 A degree three polynomial can be written as p(x) = a + bx + cx + dx3 where a, b, and d are coefficients that we would like to determine. a) Write the four linear equations for the coefficients obtained by requiring that the graph of the polynomial p(x) passes through the four points above. b) Write the augmented matrix corresponding to this system of equations and use MATLAB to solve for the coefficients. c) Write the polynomial p(x) that you found and check your work by graphing it in MATLAB and verifying that it passes through the four points. d) Rather than looking for a degree three polynomial, suppose we wanted to find a polynomial that passes through the four points and that has degree two, such as p(x) = a +bx+cx Solve the system of equations for the coefficients. What can you say about the existence and uniqueness of a degree two polynomial passing through these four points? e) Rather than looking for a degree three polynomial, suppose we wanted to find a polynomial that passes through the four points and that has degree four, such as p(x) = a +bx+cx2 + dx + ex*. Solve the system of equations for the coefficients. What can you say about the existence and uniqueness of a degree four polynomial passing through these four points? f) Suppose you had 10 points and you wanted to find a polynomial passing through each of them. What should the degree of the polynomial be to guarantee that there is exactly one such polynomial? Explain your response. Task 3. The network in Figure 1 shows the traffic flow in vehicles per hour) over several one- way streets in downtown Baltimore during a typical early afternoon. Determine the general flow pattern for the network. This means to find the traffic flow on the sections of street between AB, CB, CD, and AD. 100 South St. Calvert St. Z Lombard St. B 300+ +400 4 132 Pratt St. A D 300 600 Inner Harbor 500 Figure 1 Baltimore streets