Please find and fix my mistakes asap, the code language is in Matlab. Please write the script of code that satisfies the Matlab grader. A good solution will receive upvotes!

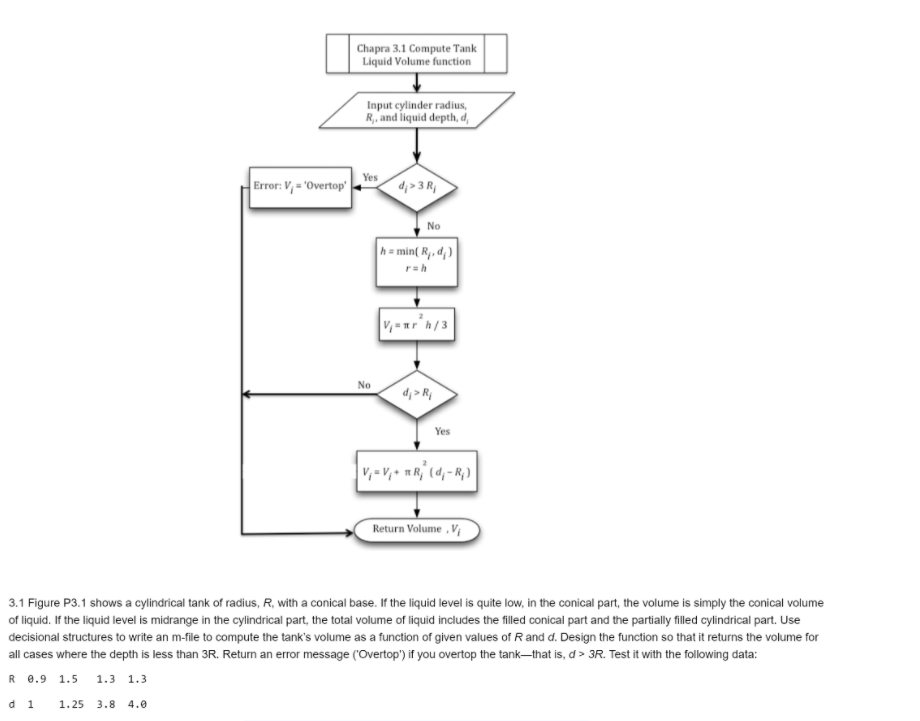
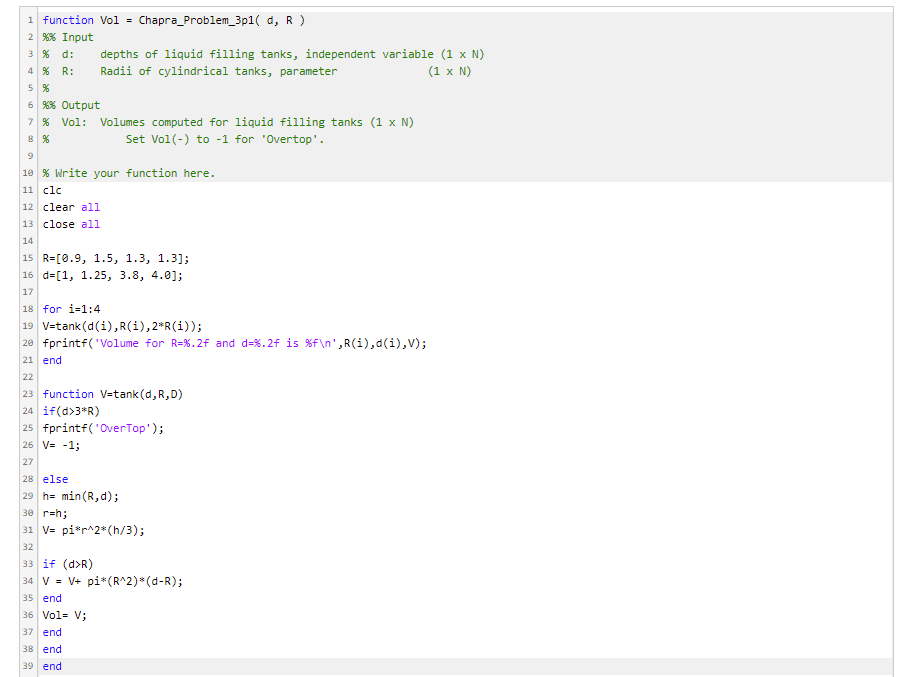
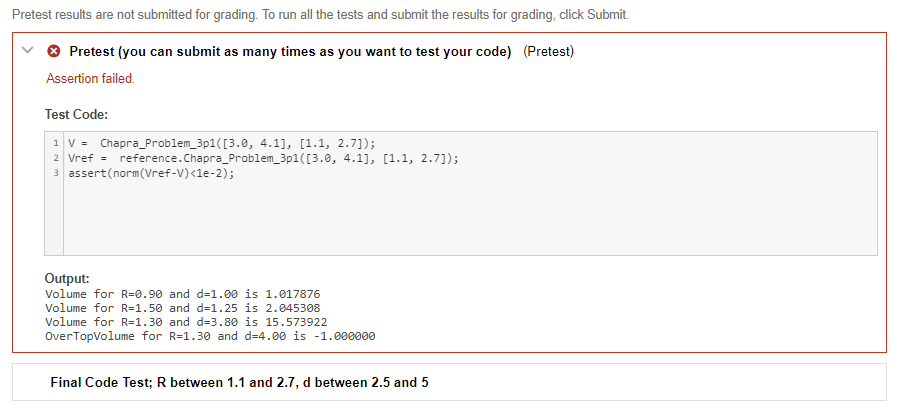
Chapra 3.1 Compute Tank Liquid Volume function Input cylinder radius R, and liquid depth, d, Yes Error: V = 'Overtop' d,> 3 R No h = min Ry, d) V-ur/3 No Yes V = V; * T R (d;-R) Return VolumeV 3.1 Figure P3.1 shows a cylindrical tank of radius, R, with a conical base. If the liquid level is quite low, in the conical part, the volume is simply the conical volume of liquid. If the liquid level is midrange in the cylindrical part, the total volume of liquid includes the filled conical part and the partially filled cylindrical part. Use decisional structures to write an m-file to compute the tank's volume as a function of given values of Rand d. Design the function so that it returns the volume for all cases where the depth is less than 3R. Return an error message ('Overtop") if you overtop the tankthat is, d> 3R. Test it with the following data: R 0.9 1.5 1.3 1.3 d 1 1.25 3.8 4.0 1 function Vol = Chapra_Problem_3p1( d, R) 2 %3 Input 3 % d: depths of liquid filling tanks, independent variable (1 x N) 4 % R: Radii of cylindrical tanks, parameter (1 x N) 5 % 6 % Output 7 % Vol: Volumes computed for liquid filling tanks (1 x N) 8 % Set Vol(-) to -1 for 'Overtop'. 9 10 % Write your function here. 11 clc 12 clear all 13 close all 14 15 R=[0.9, 1.5, 1.3, 1.3]; 16 d=[1, 1.25, 3.8, 4.0); 17 18 for i=1:4 19 V-tank (d(i),R(i),2*R(i)); 20 fprintf("Volume for R=%.2f and d=%.2f is %f ',R(1),d(i),V); 21 end 22 23 function Vatank(d,R,D) 24 if(d>3R) 25 fprintf('OverTop'); 26 V= -1; 27 28 else 29 h= min (R,d); 30 rsh; 31 V= pi*p^2*(h/3); 32 33 if (d>R) 34 V = V+ pi*(R^2)*(d-R); 35 end 36 Vol= V; 37 end 38 end 39 end Pretest results are not submitted for grading. To run all the tests and submit the results for grading, click Submit. Pretest (you can submit as many times as you want to test your code) (Pretest) Assertion failed. Test Code: 1 V = Chapra_Problem_3p1([3.0, 4.1], [1.1, 2.7]); 2 Vref = reference. Chapra_Problem_3p1([3.0, 4.1], [1.1, 2.7]); 3 assert(norm(Vref-V) 3 R No h = min Ry, d) V-ur/3 No Yes V = V; * T R (d;-R) Return VolumeV 3.1 Figure P3.1 shows a cylindrical tank of radius, R, with a conical base. If the liquid level is quite low, in the conical part, the volume is simply the conical volume of liquid. If the liquid level is midrange in the cylindrical part, the total volume of liquid includes the filled conical part and the partially filled cylindrical part. Use decisional structures to write an m-file to compute the tank's volume as a function of given values of Rand d. Design the function so that it returns the volume for all cases where the depth is less than 3R. Return an error message ('Overtop") if you overtop the tankthat is, d> 3R. Test it with the following data: R 0.9 1.5 1.3 1.3 d 1 1.25 3.8 4.0 1 function Vol = Chapra_Problem_3p1( d, R) 2 %3 Input 3 % d: depths of liquid filling tanks, independent variable (1 x N) 4 % R: Radii of cylindrical tanks, parameter (1 x N) 5 % 6 % Output 7 % Vol: Volumes computed for liquid filling tanks (1 x N) 8 % Set Vol(-) to -1 for 'Overtop'. 9 10 % Write your function here. 11 clc 12 clear all 13 close all 14 15 R=[0.9, 1.5, 1.3, 1.3]; 16 d=[1, 1.25, 3.8, 4.0); 17 18 for i=1:4 19 V-tank (d(i),R(i),2*R(i)); 20 fprintf("Volume for R=%.2f and d=%.2f is %f ',R(1),d(i),V); 21 end 22 23 function Vatank(d,R,D) 24 if(d>3R) 25 fprintf('OverTop'); 26 V= -1; 27 28 else 29 h= min (R,d); 30 rsh; 31 V= pi*p^2*(h/3); 32 33 if (d>R) 34 V = V+ pi*(R^2)*(d-R); 35 end 36 Vol= V; 37 end 38 end 39 end Pretest results are not submitted for grading. To run all the tests and submit the results for grading, click Submit. Pretest (you can submit as many times as you want to test your code) (Pretest) Assertion failed. Test Code: 1 V = Chapra_Problem_3p1([3.0, 4.1], [1.1, 2.7]); 2 Vref = reference. Chapra_Problem_3p1([3.0, 4.1], [1.1, 2.7]); 3 assert(norm(Vref-V)