Please help! I have a lab due in 7 hours and I am confused how to do this. Thank you! I will give thumbs up
Part 3: Energy Conservation in a Capacitor
Background: To transport a charge Q through a voltage increase V requires QV of energy. If it goes the other way, QV of energy is released. You might think that a capacitor with charge Q and voltage V has QV of stored energy. However, this ignores one important thing. The charge itself is what creates the voltage. Think of it this way: once half the charge has gone from the positive plate to the negative plate both the amount of charge Q and the amount of voltage V have decreased by half. The remaining charge only has half the voltage: not the full voltage. Therefore, the stored energy must be less than QV. In fact, the stored energy in a capacitor is QV/2 or CV2/2.
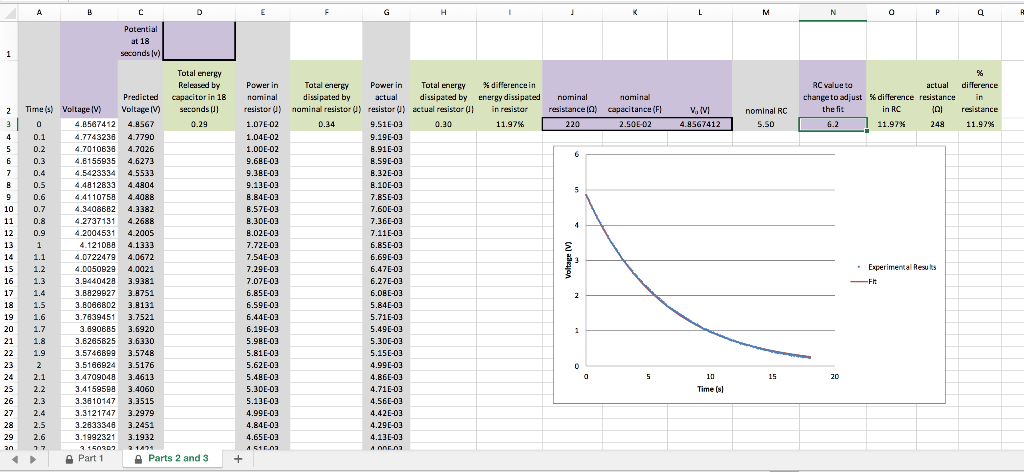
Question A) In the steps following this pitstop, you will calculate and compare the energy released by the capacitor with the energy dissipated in the resistor. However, you likely found some difference between the nominal value of RC and a slightly different one that resulted in a better fit of a line to the data. Lets assume that the capacitance of the capacitor is exactly as given by its manufacturer (25,000 uF capacitor). Cell P2 in the Excel template will use your value of RC from the fit and calculate from it a value for R that best fits your data, and cell Q2 will calculate the percent difference between the nominal and actual values for resistance. Record these values below and comment upon what could account for this difference.
Question B) Compare the energy released by the capacitor (D3 on excel sheet listed above) with the energy dissipated in the resistor. First use the value determined by the nominal resistance (F3), and then the value determined by the actual resistance (H3 on excel sheet). Which value of R works the best?
A B D G H 1 J K L M N 0 P g Potential at 18 seconds Iv) 1 nominal nominal resistance (9) capacitance (FI 220 2.50E D2 % difference in resistance 11.97% RC value to actual change to adjust % difference resistance the fit in RC 101 6.2 11.97% 248 V, AVI 4.9567412 nominal RC 5.50 2 3 4 5 6 7 7 6 5 4 Total energy Released by Predicted capacitor in 18 Voltage (V) seconds 01 4.9567 0.29 4.7790 4.7026 4.6273 4.5533 4.4804 4.4088 4.3382 4.2688 4.2005 4.1333 4.0672 4.0021 3.9381 3.8751 3.8131 3.7521 3.6920 3.6330 3.5748 3.5176 3.4613 3.4060 3.3515 3.2979 3.2451 3.1932 21A Parts 2 and 3 Time (s) Voltage IV) 0 4.6567412 0.1 4.7743238 0.2 4.7010638 0.3 4.6155935 0.4 4.5423334 0.5 4.4812833 0.6 4.4110758 0.7 4.3408662 0.8 4.2737131 0.9 4.2004531 1 4.121088 1.1 4.0722479 1.2 4.0050929 1.3 3.6440428 1.4 3.8829927 1.5 3.8066802 1.6 3.7839451 1.7 3.690665 3.6265825 1.9 3.5746889 2 3.5166924 2.1 3.4709048 2.2 3.4159588 2.3 3.3810147 2.4 3.3121747 2.5 3.2633346 2.6 3.1992321 77 3150803 Part 1 Experimental Results Power in Total energy Power in Total energy * difference in nominal dissipated by actual dissipated by energy dissipated resistor ) nominal resistor U) resistor (1) actual resistor ( in resistor 1.07E-02 0.34 9.51E-03 0.30 11.97% 1.04E-02 9.19E-03 1.00E-02 8.916-03 9.6BC-03 8.59 E-03 9.3B-03 8.320-03 9.13-03 8.10E-03 8.845-03 7.856-03 8.57E-03 7.60E-03 8.30E-03 7.360-03 8.02-03 7.11E-03 7.72-03 6.85C-03 7.54E-03 6.696-03 7.29 E-03 6.476-03 7.07-03 6.27E-03 6.85 E-03 6.OBL-03 6.59 E-03 5.84E-03 6.44E-03 5.71E-03 6.19E-03 5.49 E-03 5.98E-03 5.30E 03 5.81E-03 5.15E-03 5.626 03 4.996-03 5.4BC-03 4.86E-03 5.30E-03 4.71E-03 5.13 -03 4.56E-03 4.99E-03 4.42-03 4.84E-03 4.29E-03 4.65E-03 4.13E-03 A 51.0 A nr.Na + 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 an - Ft 2 1 0 a 5 15 20 10 Times When our capacitor discharges, where does the energy go? It goes into the resistor. The resistor dissipates the electrical energy as heat with a power of V?/R. If we integrate this power over time we get the total energy consumed in the resistor. Our Excel template has some calculations set up to let us see how the energy released by the capacitor compares to the energy lost in the resistor, over the interval of about 18 seconds. 1. To calculate the energy released by the capacitor over 18 seconds, put the value of the potential of the capacitor at 18 seconds into cell D1. In cell D3, the template will calculate the energy released according to the expression C(v?(Qt = 0 sec) - V(Qt = 18 sec)) 2 2. To find the total energy dissipated by the resistor, we approximate an integration of the power loss in the resistor by summing the product of the rate of energy use and the time interval over which it happened. Since the time steps in increments of At = 0.1 sec, in this case the integral can be approximated as a sum given as E (P *At) = energy lost in resistor. Columns E and G will calculate the power for each time step, based upon your nominal and actual resistance, and the total energy dissipated by the resistor will be calculated in cells F3 and H3, again by nominal and actual resistance, respectively. A B D G H 1 J K L M N 0 P g Potential at 18 seconds Iv) 1 nominal nominal resistance (9) capacitance (FI 220 2.50E D2 % difference in resistance 11.97% RC value to actual change to adjust % difference resistance the fit in RC 101 6.2 11.97% 248 V, AVI 4.9567412 nominal RC 5.50 2 3 4 5 6 7 7 6 5 4 Total energy Released by Predicted capacitor in 18 Voltage (V) seconds 01 4.9567 0.29 4.7790 4.7026 4.6273 4.5533 4.4804 4.4088 4.3382 4.2688 4.2005 4.1333 4.0672 4.0021 3.9381 3.8751 3.8131 3.7521 3.6920 3.6330 3.5748 3.5176 3.4613 3.4060 3.3515 3.2979 3.2451 3.1932 21A Parts 2 and 3 Time (s) Voltage IV) 0 4.6567412 0.1 4.7743238 0.2 4.7010638 0.3 4.6155935 0.4 4.5423334 0.5 4.4812833 0.6 4.4110758 0.7 4.3408662 0.8 4.2737131 0.9 4.2004531 1 4.121088 1.1 4.0722479 1.2 4.0050929 1.3 3.6440428 1.4 3.8829927 1.5 3.8066802 1.6 3.7839451 1.7 3.690665 3.6265825 1.9 3.5746889 2 3.5166924 2.1 3.4709048 2.2 3.4159588 2.3 3.3810147 2.4 3.3121747 2.5 3.2633346 2.6 3.1992321 77 3150803 Part 1 Experimental Results Power in Total energy Power in Total energy * difference in nominal dissipated by actual dissipated by energy dissipated resistor ) nominal resistor U) resistor (1) actual resistor ( in resistor 1.07E-02 0.34 9.51E-03 0.30 11.97% 1.04E-02 9.19E-03 1.00E-02 8.916-03 9.6BC-03 8.59 E-03 9.3B-03 8.320-03 9.13-03 8.10E-03 8.845-03 7.856-03 8.57E-03 7.60E-03 8.30E-03 7.360-03 8.02-03 7.11E-03 7.72-03 6.85C-03 7.54E-03 6.696-03 7.29 E-03 6.476-03 7.07-03 6.27E-03 6.85 E-03 6.OBL-03 6.59 E-03 5.84E-03 6.44E-03 5.71E-03 6.19E-03 5.49 E-03 5.98E-03 5.30E 03 5.81E-03 5.15E-03 5.626 03 4.996-03 5.4BC-03 4.86E-03 5.30E-03 4.71E-03 5.13 -03 4.56E-03 4.99E-03 4.42-03 4.84E-03 4.29E-03 4.65E-03 4.13E-03 A 51.0 A nr.Na + 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 an - Ft 2 1 0 a 5 15 20 10 Times When our capacitor discharges, where does the energy go? It goes into the resistor. The resistor dissipates the electrical energy as heat with a power of V?/R. If we integrate this power over time we get the total energy consumed in the resistor. Our Excel template has some calculations set up to let us see how the energy released by the capacitor compares to the energy lost in the resistor, over the interval of about 18 seconds. 1. To calculate the energy released by the capacitor over 18 seconds, put the value of the potential of the capacitor at 18 seconds into cell D1. In cell D3, the template will calculate the energy released according to the expression C(v?(Qt = 0 sec) - V(Qt = 18 sec)) 2 2. To find the total energy dissipated by the resistor, we approximate an integration of the power loss in the resistor by summing the product of the rate of energy use and the time interval over which it happened. Since the time steps in increments of At = 0.1 sec, in this case the integral can be approximated as a sum given as E (P *At) = energy lost in resistor. Columns E and G will calculate the power for each time step, based upon your nominal and actual resistance, and the total energy dissipated by the resistor will be calculated in cells F3 and H3, again by nominal and actual resistance, respectively
