Please help

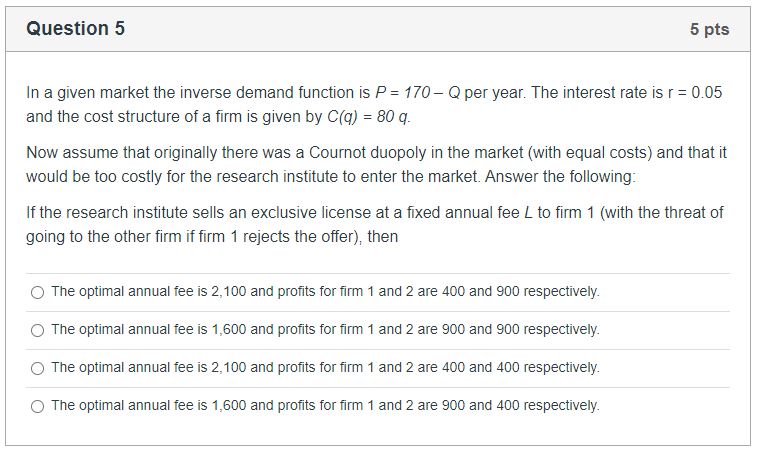
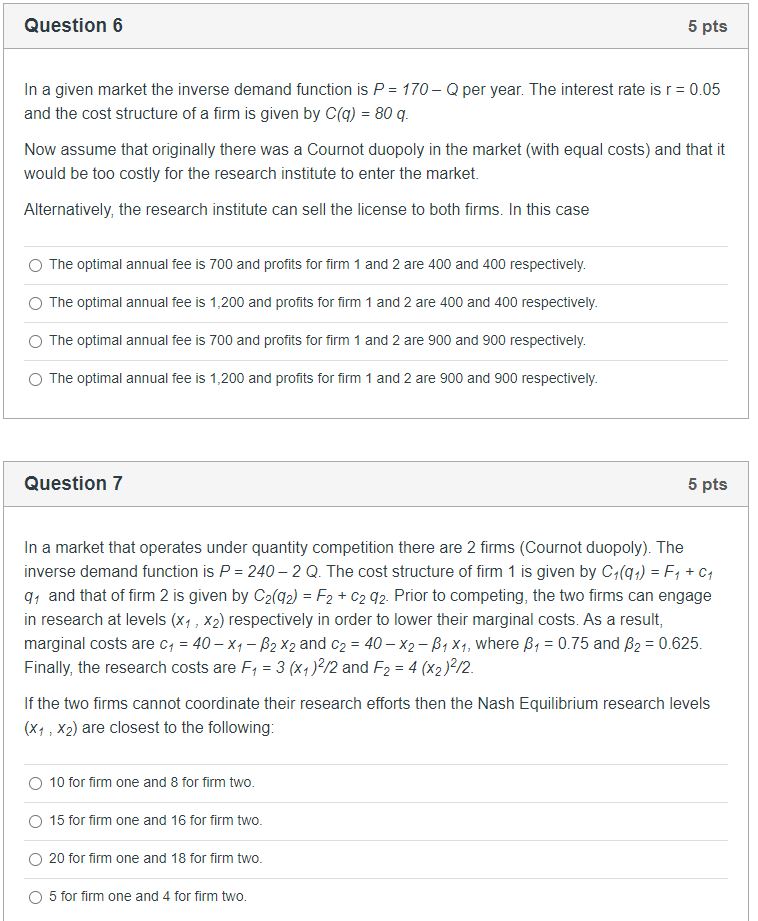
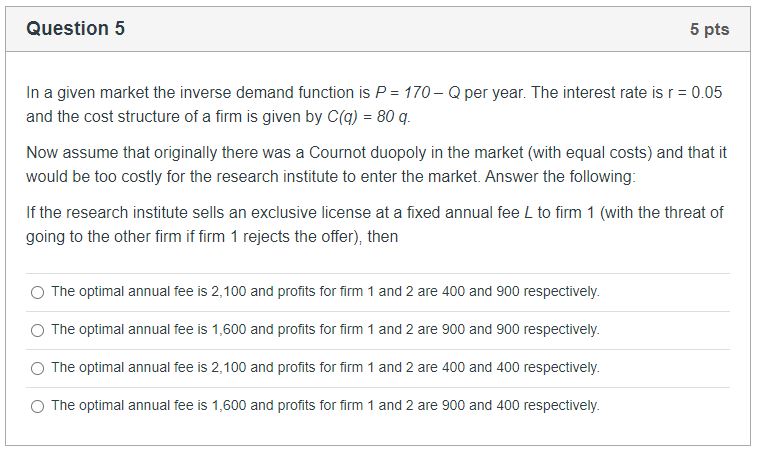
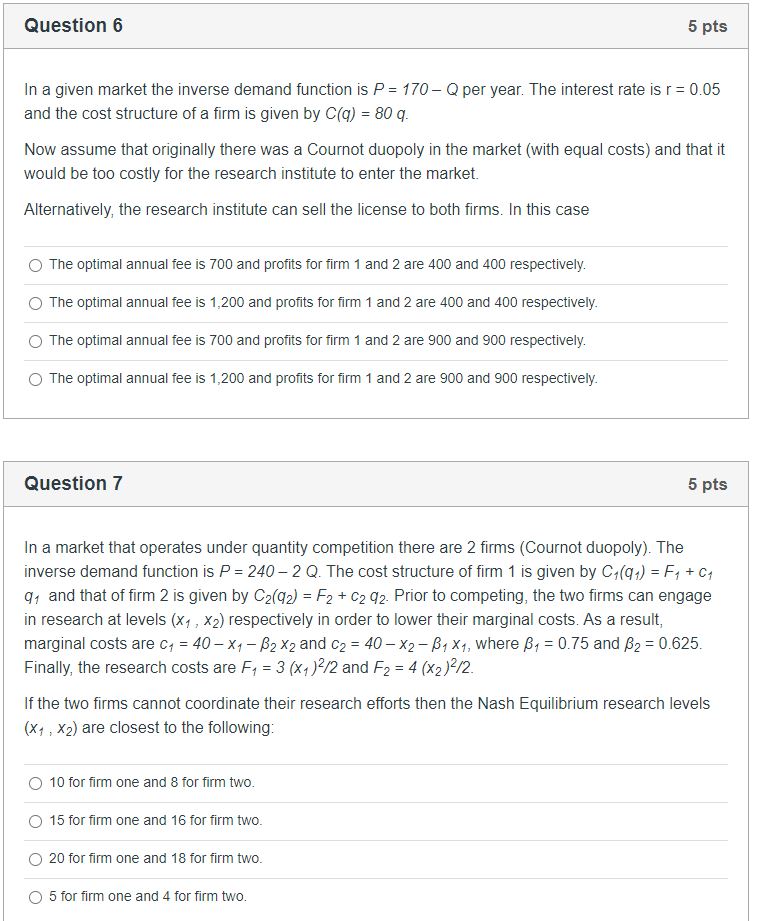
In a given market the inverse demand function is P = 1ft] Ci per year. The interest rate is r = DDS and the cost structure of a rm is given by CM) = 8t] :1}. Now assume that originally there was a |Bournot duopoly in the market {with equal costs) and that it would be too costly fer the research institute to enter the market. Answer the following: If the research institute sells an exclusive license at a xed annual fee 1'. to rm 1 (with the threat of going to the other rm if rm 1 rejects the offer). then D The optimal annual fee is 2,1(10 and prots for rm 1 and 2 are 40D and BUD respectively. 0 The optimal annual fee is LEGO and prots for rm 1 and 2 are 90D and BUD respectively. (3 The optimal annual fee is 2,113!) and prots for rm 1 and 2 are 40D and 4m] respectively. 0 The optimal annual fee is 1,600 and prots for rm 1 and 2 are SOD and 4oo respectively. In a given market the inverse demand function is P = 1m Cl per year. The interest rate is r = DDS and the cost structure of a rm is given by CM) = 3t] g. Now assume that originally there was a |Cournot duopoly in the market {with equal costs} and that it would be too costly fer the research institute to enter the market. Alternatively, the research institute can sell the license to both rms. In this case (:3: The optimal annual fee is TDD and profits for rm 1 and 2 are AGO and 400 respectively. D The optimal annual fee is 1,200 and prots for rm 1 and 2 are ACID and 4oo respectively. {:3 The optimal annual fee is TDD and prots for rm 1 and 2 are SUI] and 900 respectively. 0 The optimal annual fee is 1,2d and prots for rm 1 and 2 are 900 and 90d respectively. In a market that operates under quantity competition there are 2 rms {Cournot duopoly). The inverse demand function is P = 240 2 Q. The cost structure of rm 1 is given by {31(q1) = F1 + of of and that of rm 2 is given by {32mg} = F; + c2 o2. Prior to competing, the two rms can engage in research at levets {xi , x2} respectively in order to lower their marginal costs. As a result, marginal costs are of = 40 xi g X2 and c2 = 40 x2 31x1, where 18: 0.?5 and g 2 [1.625. Finally, the research costs are F1 = 3 (x1 FE and F2 = 4 {x2 J2ir'2. If the two rms cannot coordinate their research efforts then the Nash Equilibrium research levels (er , 1(2) are closest to the following: Cl 1G for rm one and B for lm two. 0 15 for rm one and 1Eforrm two. 0 2G for rm one and 1B for rm two. (3 5 for rm one and 4 for rm two