Please help me as much as you can!!

 

I will take all your effort to solve this problem and will give you a good rate!!!

 

Please show all the calculations in detail! 

Also, please do not copied and pasted answers from another website (Especially c_h_e_g_g)

 

Image transcription text

(1) Composite beams are made of two or more constituents, typically each with thickness of the same
order of magnitude. It is of interest to investigate the fracture behavior of such components. As an
idealization, we consider the case of a homogeneous material (either a beam or a plate) as... 
 

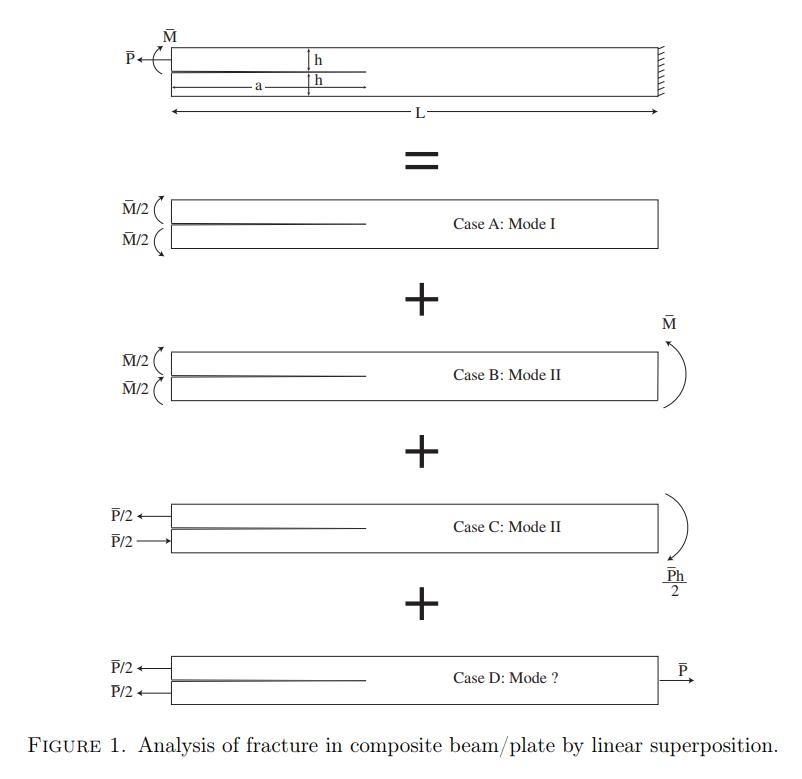
Image transcription text

M P+ - a. Th L = M/2 Case A: Mode I M/2 + M M/2( Case B: Mode II M/2 P/2 + Case C: Mode II P/2 Ph +
P/2 Case D: Mode ? P/2 + FIGURE 1. Analysis of fracture in composite beam/plate by linear
superposition.
 

(1) Composite beams are made of two or more constituents, typically each with thickness of the same order of magnitude. It is of interest to investigate the fracture behavior of such components. As an idealization, we consider the case of a homogeneous material (either a beam or a plate) as it splits along its mid-plane in response to an applied moment and applied force on the upper half, as shown in Figure 1, with cantilever conditions on the other end. The total height of the beam is 2h, the length of the crack is a, the overall length of the composite is L, and the out-of-plane depth is b. The material is assumed to be isotropic, homogeneous and linear elastic, with E = E/(1-2) for plane strain conditions (i.e. b> a) and E = E for plane stress conditions (i.e. b < < < a), where E is the Young's modulus and vis Poisson's ratio. The applied moment and force are normalized in Figure 1 as M = M/b and P = P/b, respectively. From dimensional considerations, the Mode I and Mode II stress intensity factors must have the functional form M KI=C1 + C h KII P h M P C33C41 h hz Find the constants C1, C2, C3, and c4 by calculating the energy release rate defined as G = (-1/b)(n/a), where is the potential energy of the system as a function of crack length. Also recall the Irwin relationship G = (1/E)(K + K). Typically it is not possible to determine unambiguously the values of K, and KII based upon energy methods alone; however in this case the problem can be decomposed into the sum of four simpler problems via linear superposition as shown in Figure 1. Thus, the constants can be determined individually by recourse to solution of Case A, Case B, Case C and Case D. (Hint: For each case, decompose the domain of the problem into three parts: top beam, bottom beam and unsplit beam. Sum the potential energies in each of the three parts of the domain to determine the overall potential energy.)