Please help me for this question. Thank you so much!
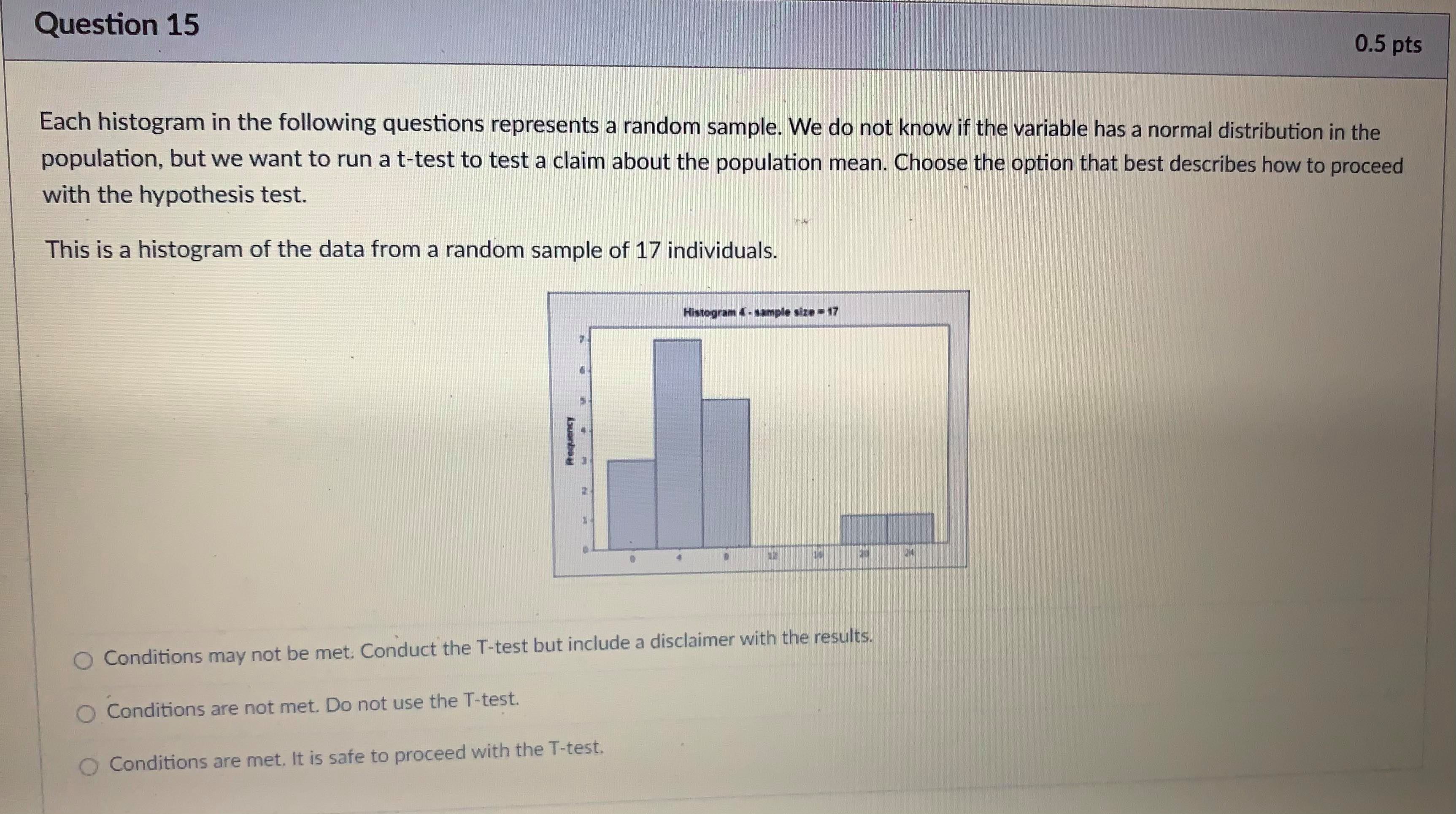
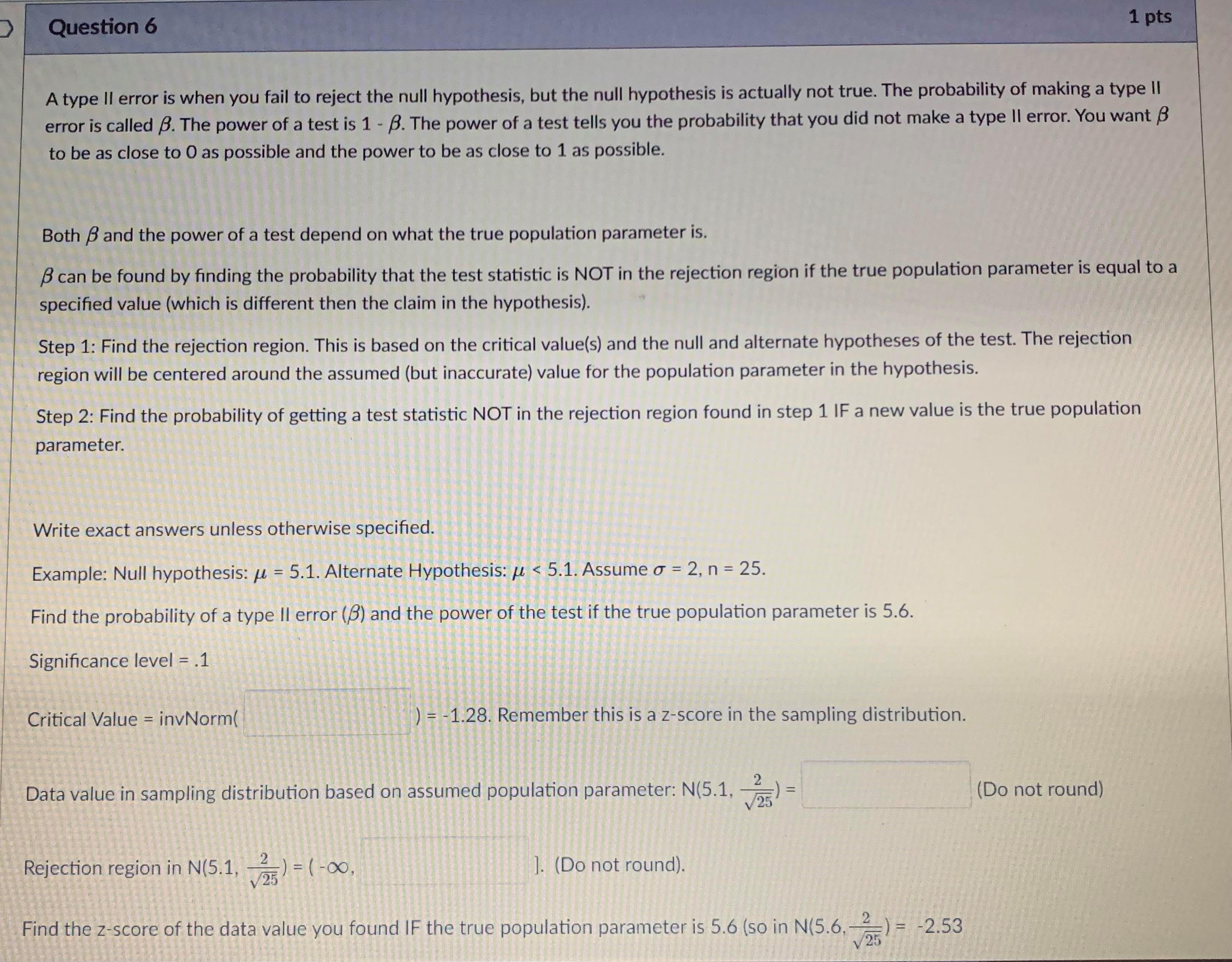
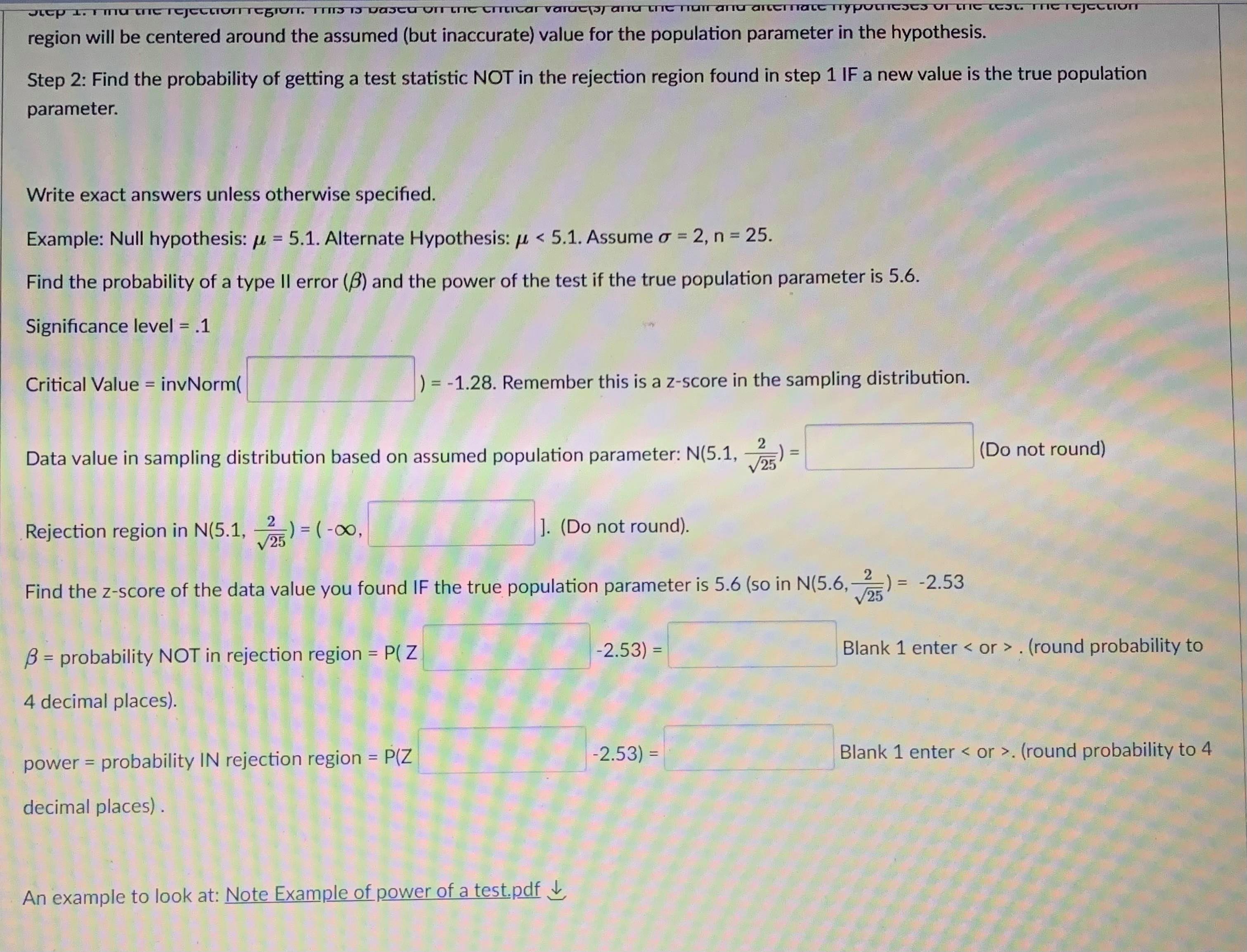
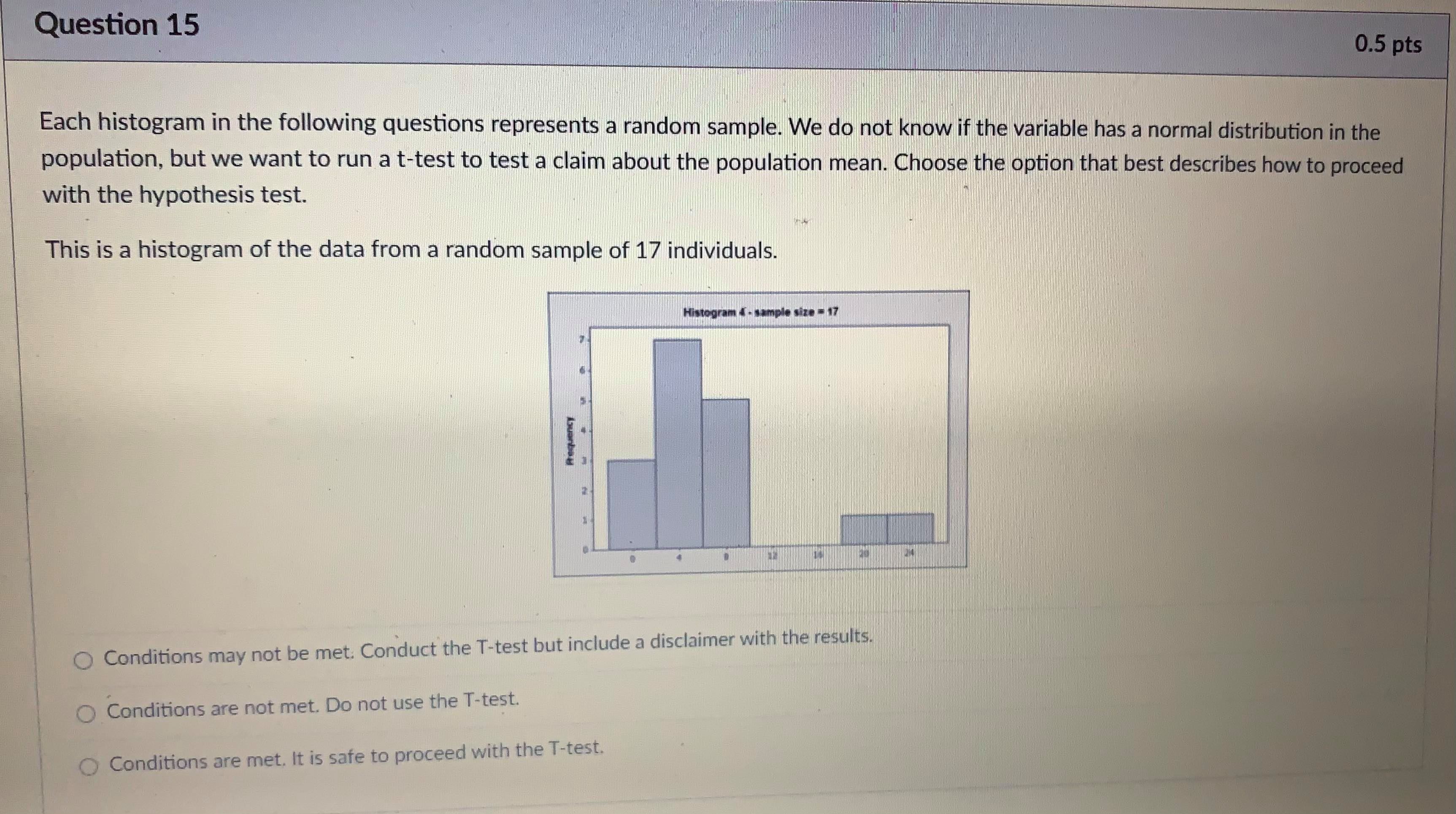
Question 5 1 pts A type II error is when you fail to reject the null hypothesis, but the null hypothesis is actually not true. The probability of making a type II error is called B. The power of a test is 1 - B. The power of a test tells you the probability that you did not make a type II error. You want B to be as close to O as possible and the power to be as close to 1 as possible. Both B and the power of a test depend on what the true population parameter is. B can be found by finding the probability that the test statistic is NOT in the rejection region if the true population parameter is equal to a specified value. Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / > 5.1. Assume o = 2, n = 25. Find the probability of a type II error (8) and the power of the test if the true population parameter is 5.6. Significance level = .05. Critical Value = invNorm(0.95) = I Remember this is a z-score in the sampling distribution. Round to 2 decimal places. Data value in sampling distribution based on assumed population parameter: N(5.1, -) = V25 Do not round) Rejection region in N(5.1, -2 V25) = [ oo). (Do not round) Find the z-score of the data value you found IF the true population parameter is 5.6 (so in N(5.6, -2 V25specmea value. Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / > 5.1. Assume o = 2, n = 25. Find the probability of a type II error (B) and the power of the test if the true population parameter is 5.6. Significance level = .05. Critical Value = invNorm(0.95) = Remember this is a z-score in the sampling distribution. Round to 2 decimal places. Data value in sampling distribution based on assumed population parameter: N(5.1, V25 Do not round) Rejection region in N(5.1, -) = [ oo). (Do not round) Find the z-score of the data value you found IF the true population parameter is 5.6 (so in N(5.6, -2 V25 B = probability NOT in rejection region = P( Z (round probability to 4 decimal places) .Question 6 1 pts A type II error is when you fail to reject the null hypothesis, but the null hypothesis is actually not true. The probability of making a type II error is called B. The power of a test is 1 - B. The power of a test tells you the probability that you did not make a type II error. You want B to be as close to O as possible and the power to be as close to 1 as possible. Both B and the power of a test depend on what the true population parameter is. B can be found by finding the probability that the test statistic is NOT in the rejection region if the true population parameter is equal to a specified value (which is different then the claim in the hypothesis). Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / . (round probability to 4 decimal places). power = probability IN rejection region = P(Z -2.53) = Blank 1 enter . (round probability to 4 decimal places) . An example to look at: Note Example of power of a test.pdf &Question 15 0.5 pts Each histogram in the following questions represents a random sample. We do not know if the variable has a normal distribution in the population, but we want to run a t-test to test a claim about the population mean. Choose the option that best describes how to proceed with the hypothesis test. This is a histogram of the data from a random sample of 17 individuals. Histogram & - sample size = 17 Requen Conditions may not be met. Conduct the T-test but include a disclaimer with the results. Conditions are not met. Do not use the T-test. Conditions are met. It is safe to proceed with the T-test