PLEASE HELP ME IN SOLVING THIS.

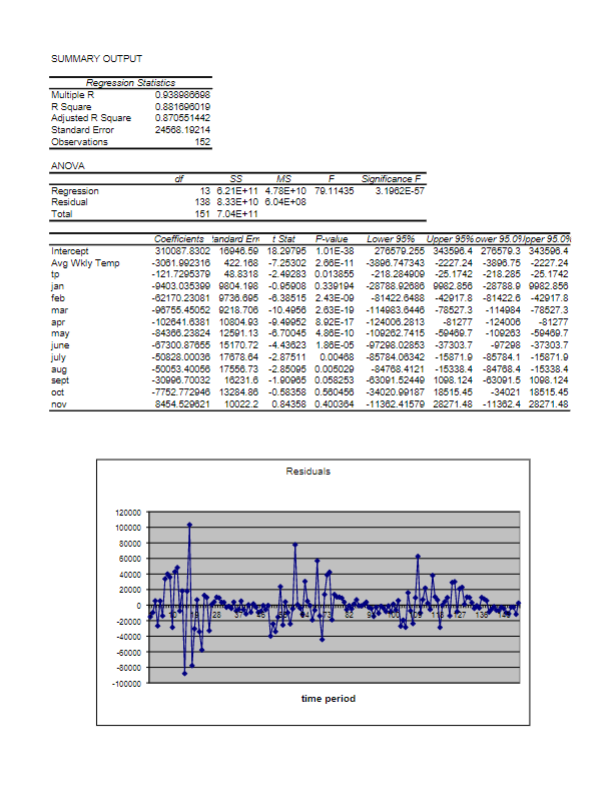
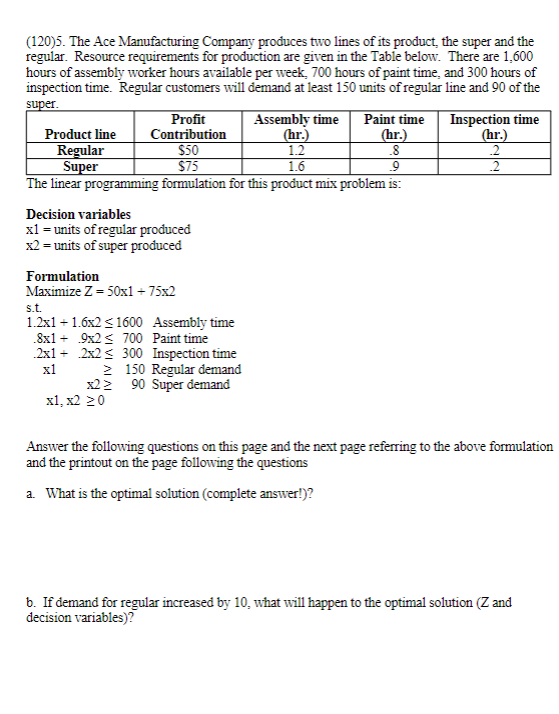
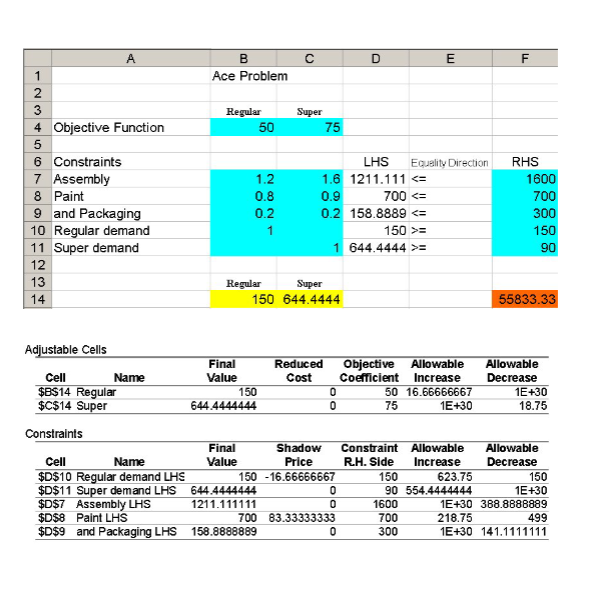
(40)1. A service has five tasks, performed in sequence. In the instance when there is more than one worker assigned to a task, each worker performs the entire task and they both can be working on different "items" at the same time. a. What is the capacity (hourly) of the process as a whole? b. What is the bottleneck of the process? c. What is the throughput time (assuming no wait time)? d. Where would you expect customers to wait? (70)2. Artie Siegel, an MBA student, has been having problems balancing his checkbook. His monthly income is derived from a graduate research assistantship; however, he also makes extra money in most months by tutoring undergraduates in their quantitative analysis course. His historical chances of various income levels are shown in the following table: *Assume that this income is received at the beginning of each month. Siegel's expenditures also vary from month to month, and he estimates that they will follow this distribution: He begins his final year with $600 in his checking account. Simulate the entire year (12 months) on the next page and discuss Siegel's financial picture, i.e., will he be able to keep his head above water--(out of debt)? What is his expected average profit for the 12 months? Use the random numbers below. Random numbers for Income and Expenses (90)3. Hands-on is a company that features a product line of winter gloves for the entire family-men, women, and children. They want to decide what mix of these three types of gloves to produce. The Hands-on's manufacturing labor force is unionized. Each full-time employee works a 40hour week. In addition, by union contract, the number of full-time employees can never drop below 20. Nonunion, part-time workers also can be hired with the following union-imposed restrictions: (1) Each part-time worker works 20 hours per week, and; (2) There must be at least two full-time employees for each part-time employee. In terms of the manufacturing process, all three types of gloves are made out of the same 100 percent genuine cowhide leather. Hands-on has a long-term contract with a supplier of the leather and receives a 5,000 square-foot shipment of material each week. The material requirements and labor requirements, along with the gross profit per glove sold (Not considering labor costs), are given in the following table below: Each full-time employee earns $13 per hour, while each part-time employee earns $10 per hour. Management wishes to know what mix of each of the three types of gloves to produce per week, as well as how many full-time and part-time workers to employ while they would like to maximize their net profit - their gross profit from sales minus their labor costs. Formulate a linear programming model to determine the best mix of gloves and employees to have to maxmize their net profit. (DO NOT attempt to solve.) Briefly identify/describe each: decision variables, constraints and the objective function. (STANDARD FORM) Answer the following multiple-choice questions: Constraints are: A. quantities to be maximized in a linear programming model. B. quantities to be minimized in a linear programming model. C. restrictions that limit the settings of the decision variables. D. input variables that can be controlled during optimization. A(n) solution satisfies all the constraint expressions simultaneously. A. feasible B. objective C. infeasible D. extreme (150)4. HBK , a food industry company wants to build a forecasting model to predict the sales of its hot beverage. HBK had the last weekly sales for the past 152 weeks. Using the time series components for trend (variable called tp) and seasonal-monthly dummy variables (using Dec as a baseline) and the causal variable of average weekly temperature HBK management build the model on the following page. Note the average hot-beverage weekly sales is $91,500. a. Evaluate the model on the following page, i.e., is it a good model? If so, why, or if not, why? Consider all the appropriate tests, use =0.05 for t test and =0.05 for F test. Notice on the following page is a plot of the residuals. DO ALL APPROPRIATE TESTS-COMIPLETELY!!!! SUMMARY OUTPUT b. If you believe the model is OKAY, provide at least two reasons to justify your belief. On the other hand, if you believe the model is not OKAY, provide suggestions on how you would improve the model. c. Ranking the order of the months in terms of their impact on weekly sales, i.e., which month has the highest expected weekly sales, next highest, and which are the lowest and second lowest? Hirhart * =21 (d). Show how you will code the dummy variables in this model, in other words fill in 13 rows with your dummy variables in the table below. (the first column, Month, tells you what month it is). (e). What is the model's predicted value or forecast for time period 20 , which is August, and the average monthly temperature is 80 ? (f). Answer the following multiple-choice questions: A set of observations on a variable measured at successive points in time or over successive periods of time constitutes a A. geometric series B. time invariant set C. time series D. logarithmic series With reference to time series data patterns, a cyclical pattern is the component of the time series that: A. shows a periodic pattern over one year or less. B. does not vary with respect to time. C. results in periodic above-trend and below-trend behavior of the time series lasting more than one year. D. is characterized by a linear variation of the dependent variable with respect to time. (120)5. The Ace Manufacturing Company produces two lines of its product, the super and the regular. Resource requirements for production are given in the Table below. There are 1,600 hours of assembly worker hours available per week, 700 hours of paint time, and 300 hours of inspection time. Regular customers will demand at least 150 units of regular line and 90 of the suner The linear programming formulation for this product mix problem is: Decision variables x1 = units of regular produced x2= units of super produced Formulation Maximize Z=50x1+75x2 s.t. 1.21+1.621600 Assembly time .81+.92700 Paint time .21+.22300 Inspection time x1150 Regular demand x2 x1,x20 90 Super demand Answer the following questions on this page and the next page referring to the above formulation and the printout on the page following the questions a. What is the optimal solution (complete answer!)? b. If demand for regular increased by 10 , what will happen to the optimal solution ( Z and decision variables)? c. If demand for super increased by 10 , what will happen to the optimal solution ( Z and decision variables)? d. If the profit contribution of regular decreased to 30 , what will happen to the optimal solution ( Z and decision variables)? e. If the profit contribution of super decreased to 55 , what will happen to the optimal solution ( Z and decision variables)? Adjustable Cells \begin{tabular}{lccrrrr} \hline Cell & Name & FinalValue & ReducedCost & ObjectiveCoefficient & AllowableIncrease & AllowableDecrease \\ \hline$B14 Regular & 150 & & 0 & 50 & 16.66666667 & 1E+30 \\ $C$14 Super & 644.4444444 & & 0 & 75 & 1E+30 & 18.75 \\ \hline \end{tabular} Constraints \begin{tabular}{lcrrrrrr} \hline Cell & Name & FinalValue & ShadowPrice & ConstraintR.H.Side & AllowableIncrease & AllowableDecrease \\ \hline \$D\$10 Regular demand LHS & 150 & -16.66666667 & 150 & 623.75 & 150 \\ \hline \$D\$11 Super demand LHS & 644.4444444 & 0 & 90 & 554.4444444 & 1E+30 \\ \hline \$D\$7 & Assembly LHS & 1211.111111 & 0 & 1600 & 1E+30 & 388.8888889 \\ \$D\$8 & Paint LHS & 700 & 83.33333333 & 700 & 218.75 & 499 \\ \hline \$D\$9 & and Packaging LHS & 158.8888889 & 0 & 300 & 1E+30 & 141.1111111 \\ \hline \end{tabular} (20)6. Given the following benefits/characteristics of a Jesuit Education, match the characteristic that fits regarding Data Ethics (DE) and or Data Integrity (DI). (Place DE or DI in the space provided) Pays special attention to values, ethical issues, and development of moral character Stresses the importance of social and environmental justice Develops responsible citizens who are sensitive to the needs of our time Encourages critical, analytical, and creative approaches to solving problems Inspires students to change society and the world for the better