Please help me solve questions 8th,9th, and 10th.

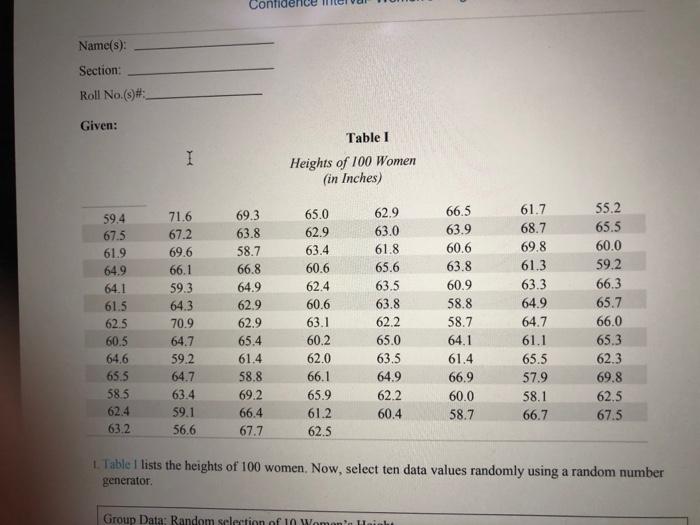
8 Some students think that a 90% confidence interval contains 90% of the data. (a) Go back to Table I(the heights of women) and highlight in yellow each of the 100 women's height that lie within the confidence interval that you generated based on that data. Count the number of heights that you have highlighted.

Answer:

Number of 100 women's that lie within YOUR confidence interval: ____________ (b) What percent is this, in one decimal point? _______________

(c) Is this percent close to 90%?

Very Close _______ Somewhat close _________ Not very close ____________

9. Explain clearly and completely why it does not make sense to count data values that lie in a confidence interval. Think about the random variable that is being used in the problem. This is the heart of this assignment. Be thoughtful in your response!

10. Suppose you obtained the heights of ten women and calculated a confidence interval from this information. Without knowing the population mean ?, would you have any way knowing for certain if your interval actually contained the value ?? Why and why not?

Confidence Name(s): Section: Roll No.(s)#: Given: Table I Heights of 100 Women (in Inches) 59.4 71.6 69.3 65.0 62.9 66.5 61.7 55.2 67.5 67.2 63.8 62.9 63.0 63.9 68.7 65.5 61.9 69.6 58.7 63.4 61.8 60.6 69.8 60.0 64.9 66.1 66.8 60.6 65.6 63.8 61.3 59.2 64.1 59.3 64.9 62.4 63.5 60.9 63.3 66.3 61.5 64.3 62.9 60.6 63.8 58.8 64.9 65.7 62.5 70.9 62.9 63.1 62.2 58.7 64.7 66.0 60.5 64.7 65.4 60.2 65.0 64.1 61.1 65.3 64.6 59.2 61.4 62.0 63.5 61.4 65.5 62.3 65.5 64.7 58.8 66.1 64.9 66.9 57.9 69.8 58 5 63.4 69.2 65.9 62.2 60.0 58.1 624 62.5 59.1 66.4 61.2 60.4 58.7 63.2 66.7 56.6 67.5 67.7 62.5 1. Table I lists the heights of 100 women. Now, select ten data values randomly using a random number generator. Group Data: Random s4. Calculate the population mean and calculate its value to one decimal point 100 women's height listed in Table L Population mean: = Now answer the following questions using the results shown in the Table II below. Table II 90% Confidence Interval for Heights of Women (in inches) Constructed by a previous class (61.2,64.6) (61.6.65.0) (64. 1,64.6) (61.4,64.9) (59.1,62.6) (63.3,66.8) (63.0,66.4) (60.5.63.9) (62.2,65.6) (63.9,66.1) (60.3,63.7) (56.9,60.3) (61.6,64.6) (65.5,69.0) (62.7.66.2) (61.2,64.7) (63.3,64.4) (61.7,65.1) (61.0.64.3) (60.5,63.9) (61.6,65.0) (62.1,64.6) Questions 1. Define the random variable, X: 2. Define the random variable: X: 3. Using Table II, the class list of confidence interval, highlight the confidence intervals that actually contain the true population mean . How many intervals did you highlight?7. When we construct a 9070 true population mean lies within the confidence interval. Using complete sentences, explain what we mean by this phrase. Answer: 8. Some students think that a 90% confidence interval contains 90% of the data. (a) Go back to Table I(the heights of women) and highlight in yellow each of the 100 women's height that lie within the confidence interval that you generated based on that data. Count the number of heights that you have highlighted. Answer: Number of 100 women's that lie within YOUR confidence interval: (b) What percent is this, in one decimal point? (c) Is this percent close to 90%? Very Close Somewhat close Not very close 9. Explain clearly and completely why it does not make sense to count data values that lie in a confidence interval. Think about the random variable that is being used in the problem. This is the heart of this assignment. Be thoughtful in your response! 10, Suppose you obtained the heights of ten women and calculated a confidence interval from this information. Without knowing the population mean , would you have any way knowing for certain if your interval actually contained the value #? Why and why not