Please help me solve the questions below. Thanks

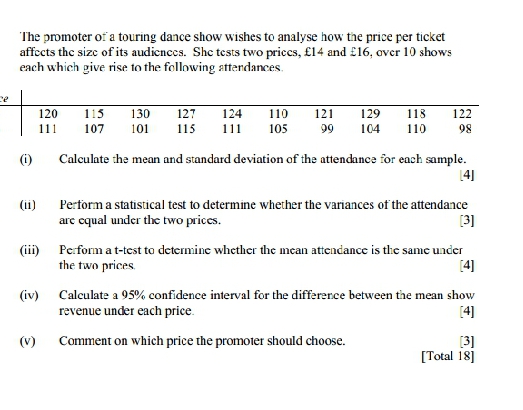
The promoter of a touring dance show wishes to analyse how the price per ticket affects the size of its audiences. She tests two prices, f14 and $16, over 10 shows each which give rise to the following attendances. 120 115 130 127 124 110 121 129 113 122 111 107 101 115 111 105 99 104 110 08 (1) Calculate the mean and standard deviation of the attendance for each sample. (41 (ii) Perform a statistical test to determine whether the variances of the attendance are equal under the two prices. [E] (iii Perform a t-test to determine whether the mean attendance is the same under the two prices [4] (iv) Calculate a 95% confidence interval for the difference between the mean show revenue under each price. (4] (v) Comment on which price the promoter should choose. 13] [Total 18]The following data (x) give the acidity (in appropriate units) of three different varieties of grape. Variety Mean Variance 8 7 18 15 12.0 28.7 90 74 200 122 121.5 3137.0 897 493 B12 365 641.8 64284.9 A wine maker wants to test whether there are differences in the mean acidity level of the three varieties and wishes to use analysis of variance (ANOVA) methodology. (i) Explain why ANOVA should not be used for the data as given in the table above. [2] A statistician suggests two transformations of the original data: the natural logarithm, y = In(x), and the square root, z = v.x. These give the following summary statistics: y = In(X) z=Vx Variety Mean Variance Mean Variance 2.4075 0.2136 3.3975 0.5046 4.7250 0.1892 10.8200 5.9242 6.4000 0.1800 24.9425 25.4567 The wine maker then decides to use the natural logarithm transformation (y) of the original data. (ii) Justify the wine maker's choice of data transformation for performing the analysis. [1] (iii) Ferform ANOVA on the transformed data, y, to investigate possible differences in the mean acidity level of the three grape varieties and state your conclusions. [6] (iv) Calculate 95% confidence intervals for the mean values of each of the three varieties on the original scale, based on the ANOVA performed on the transformed values. [61 (v) Comment on the intervals obtained in part (iv) in relation to your conclusion in part (iii). [2] [Total 17]