
Please help me with this question from the "p-values versus significance level (and Type I and II errors)" lesson. Thank you so much!!!
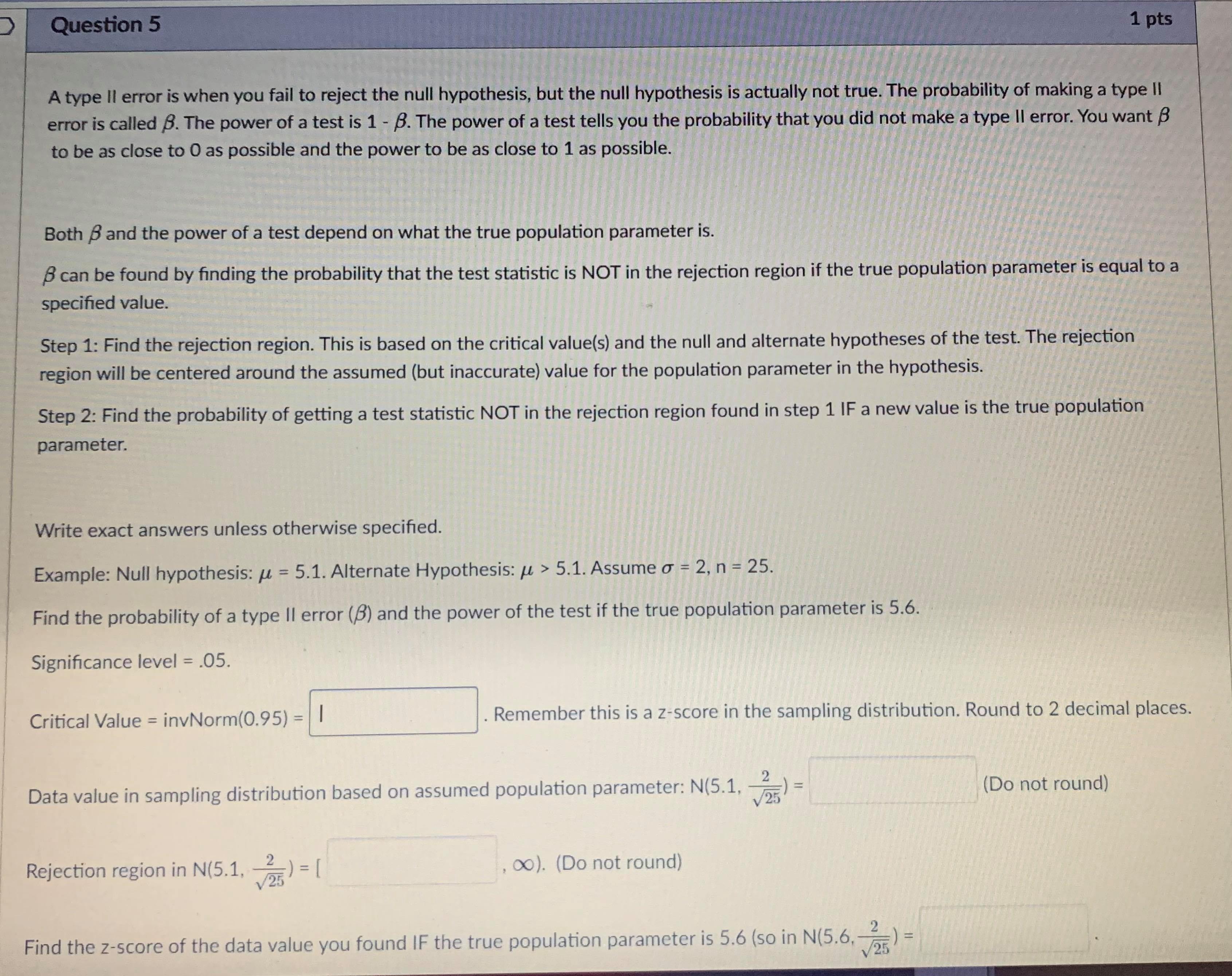
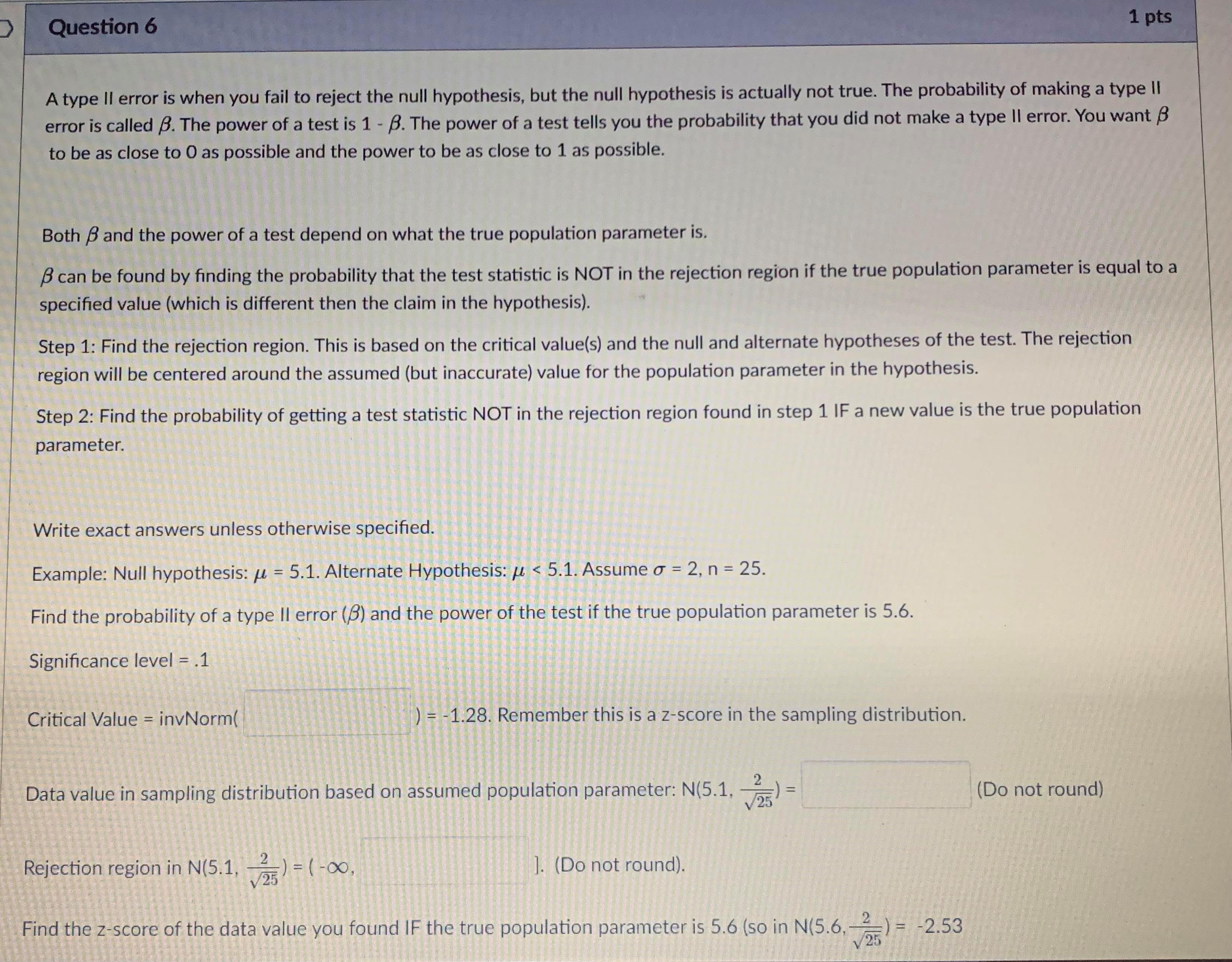
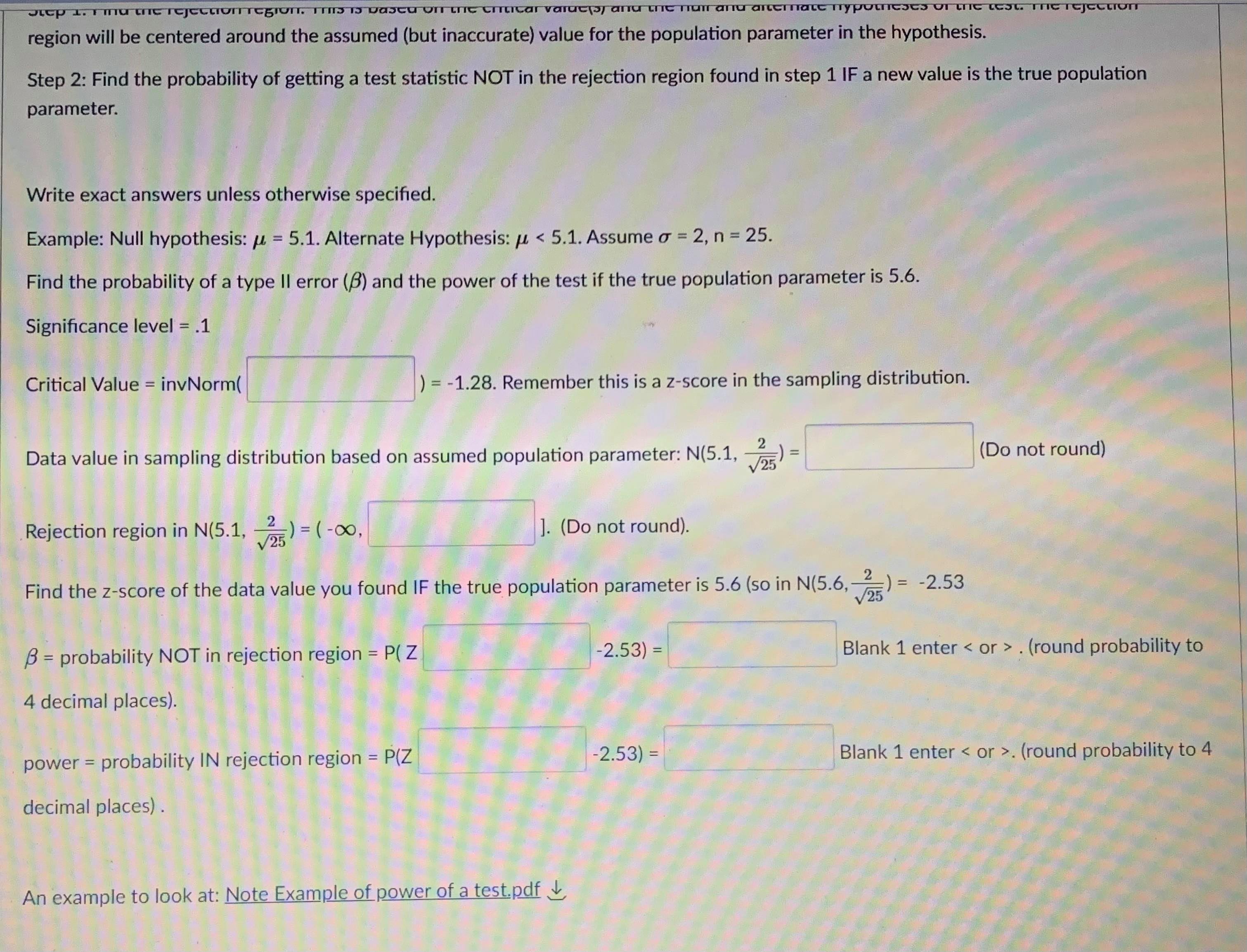
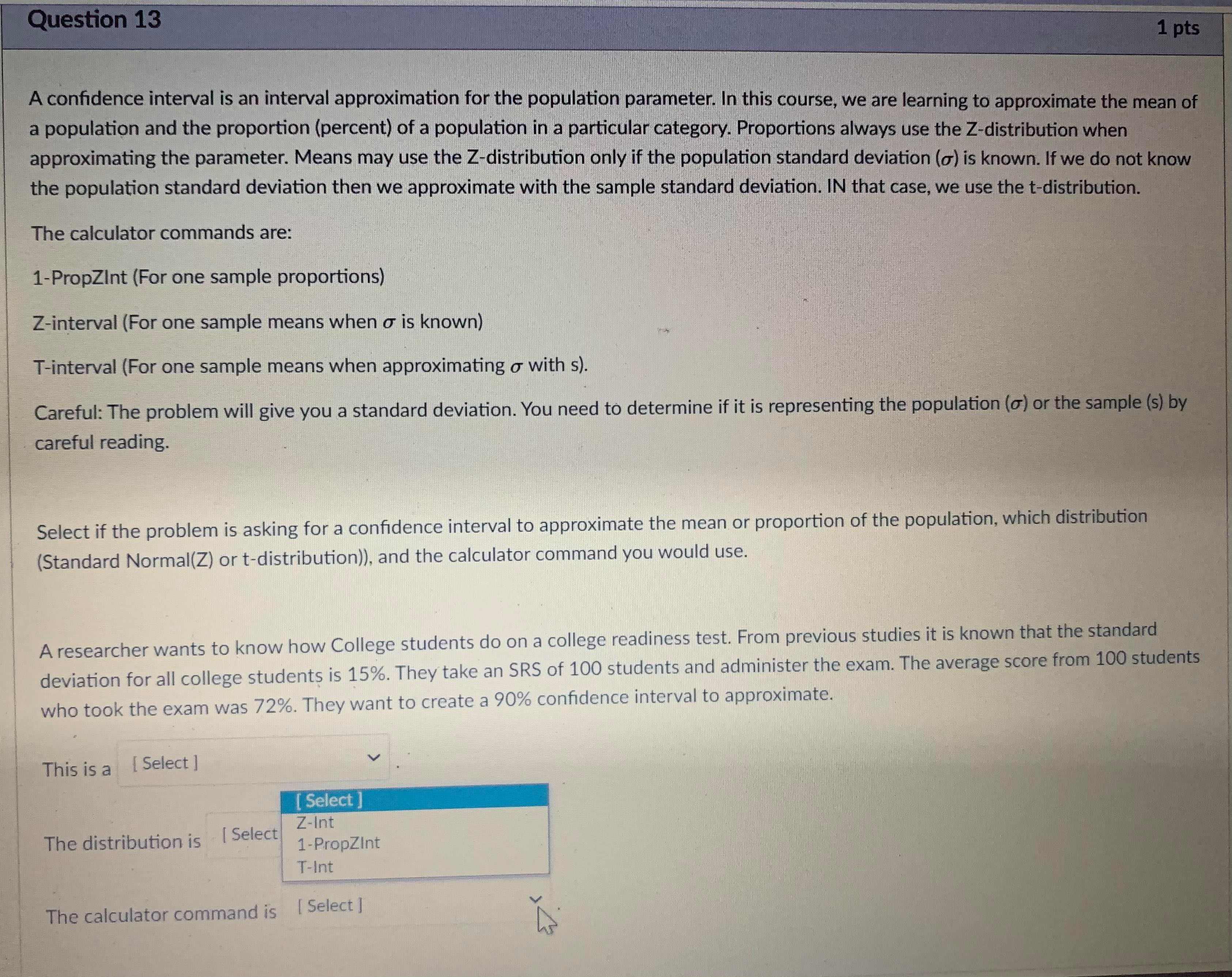
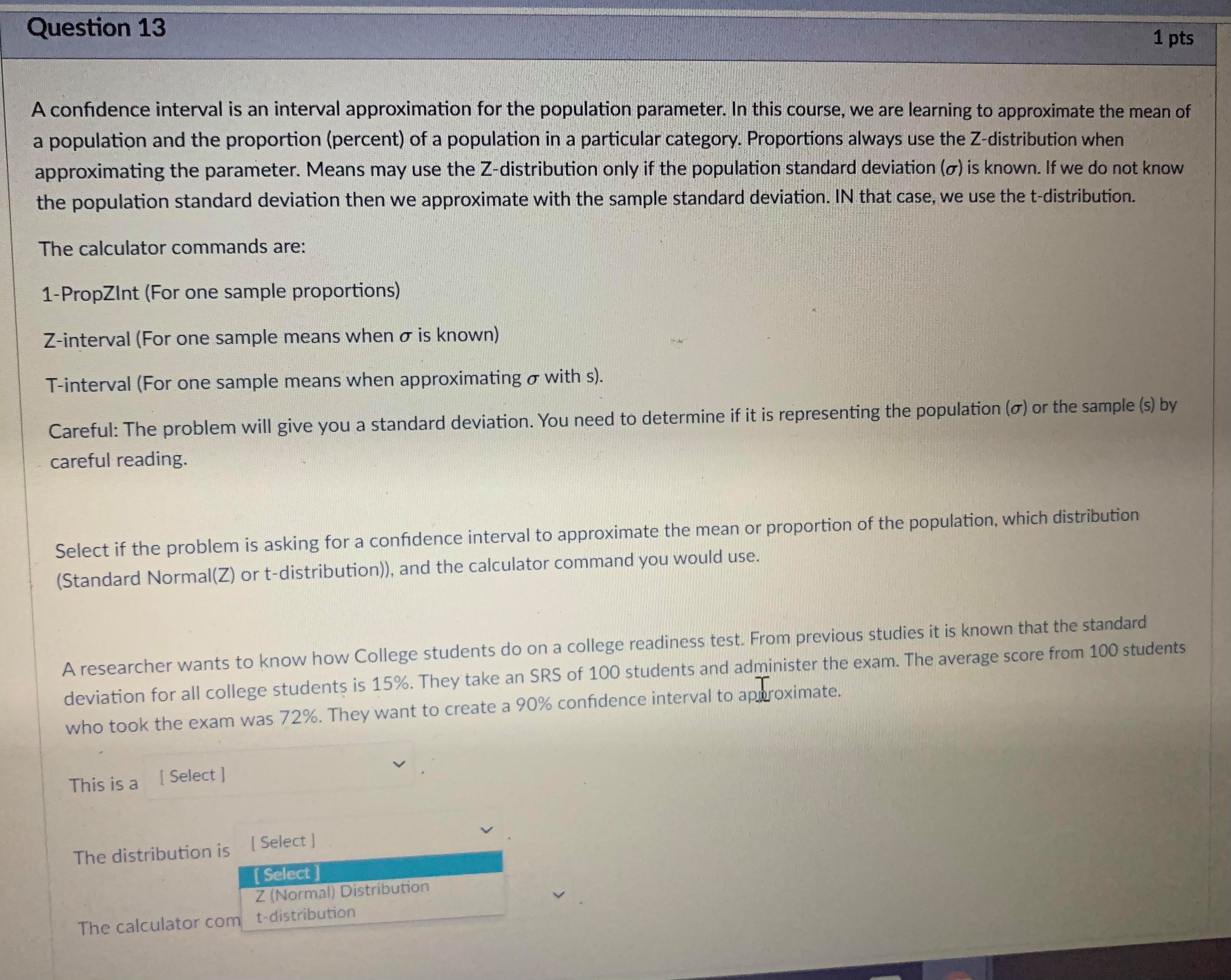
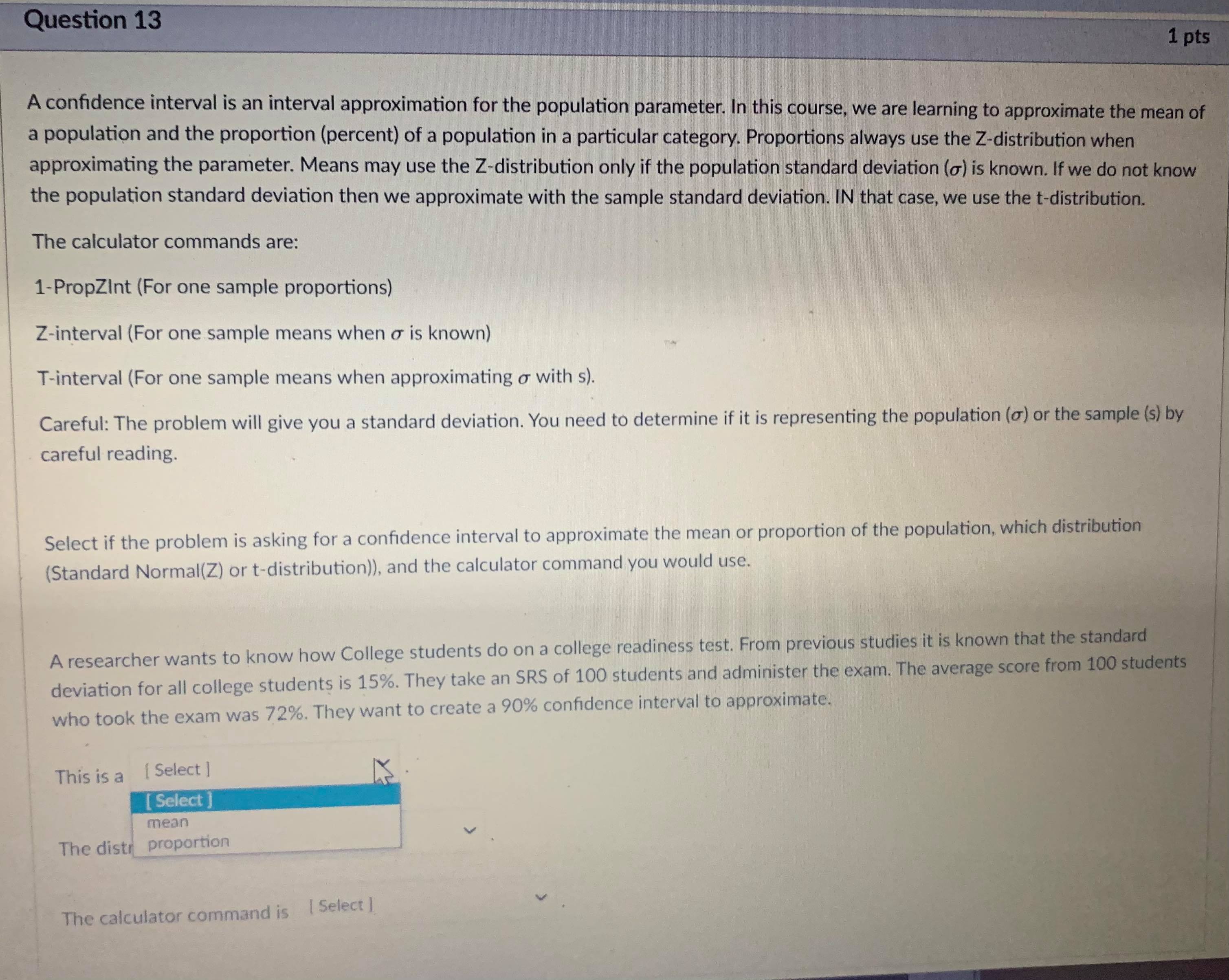
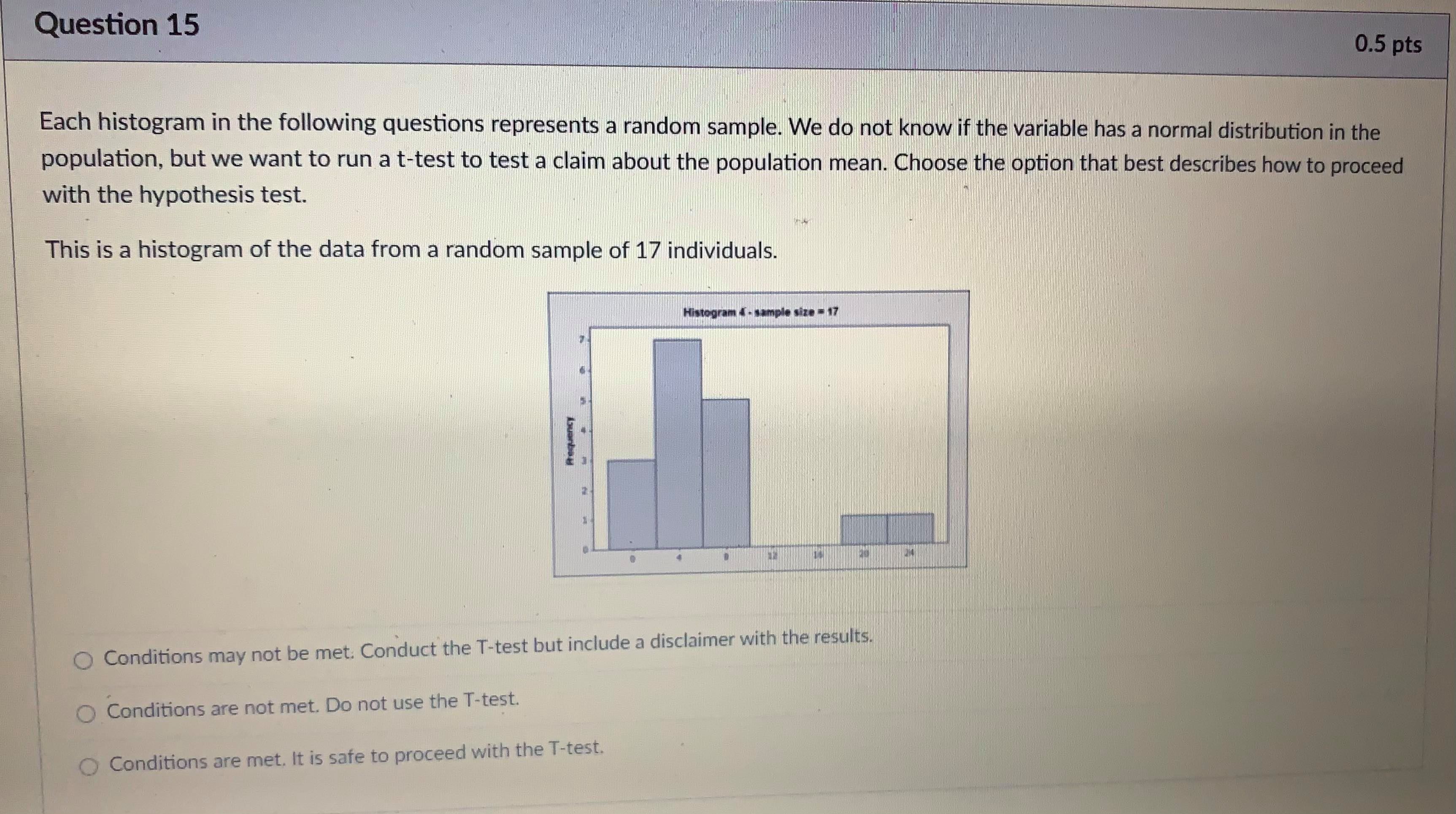
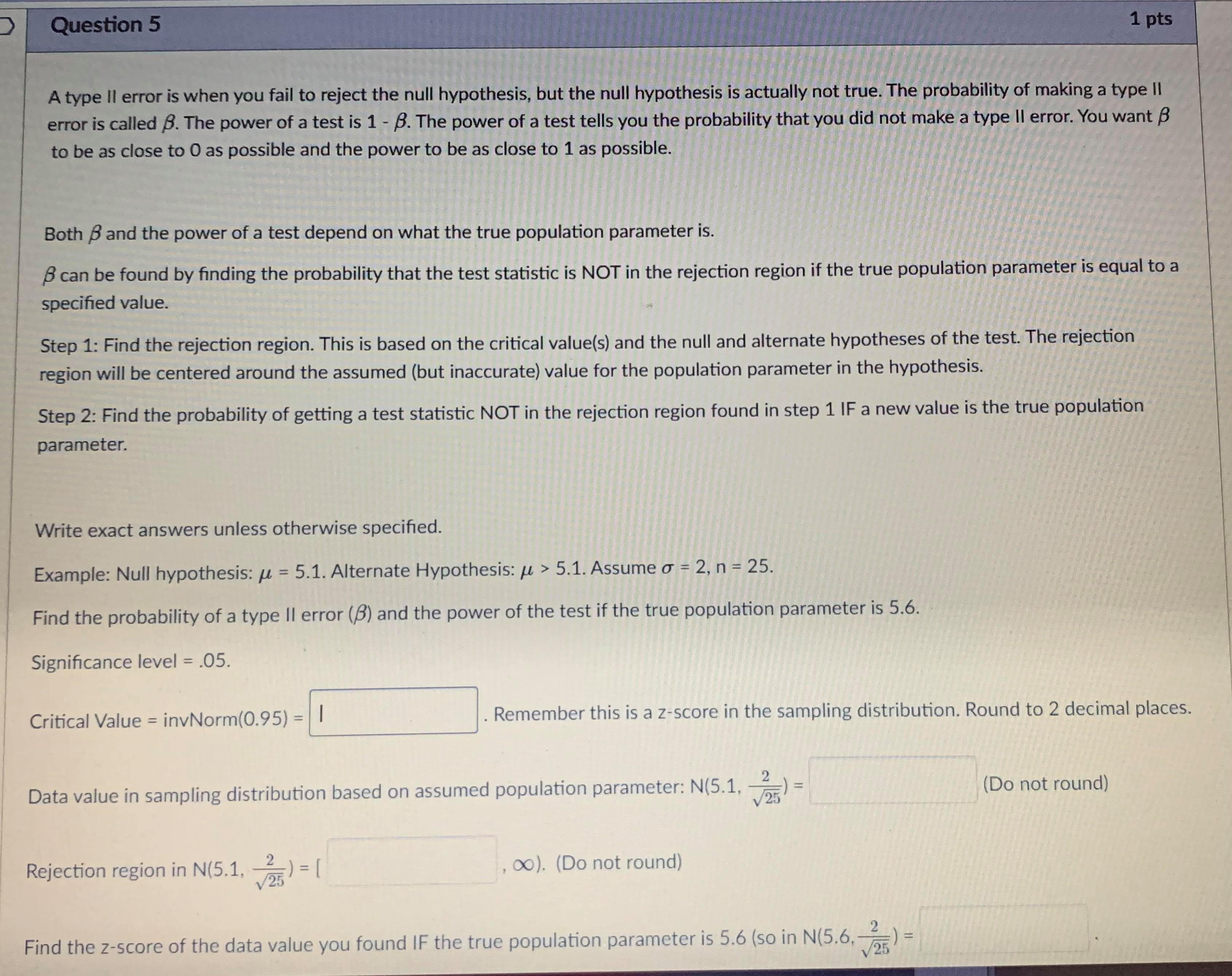
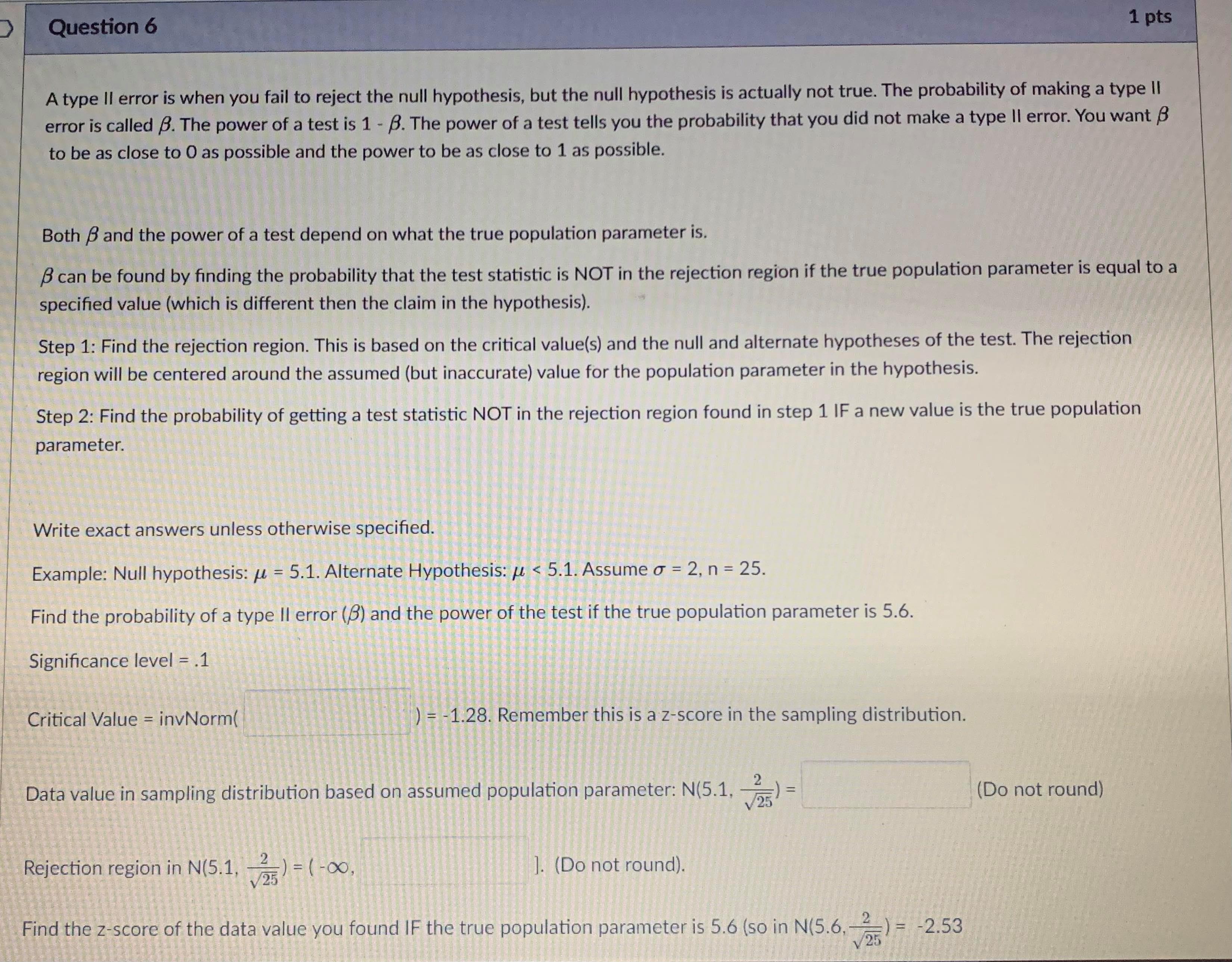
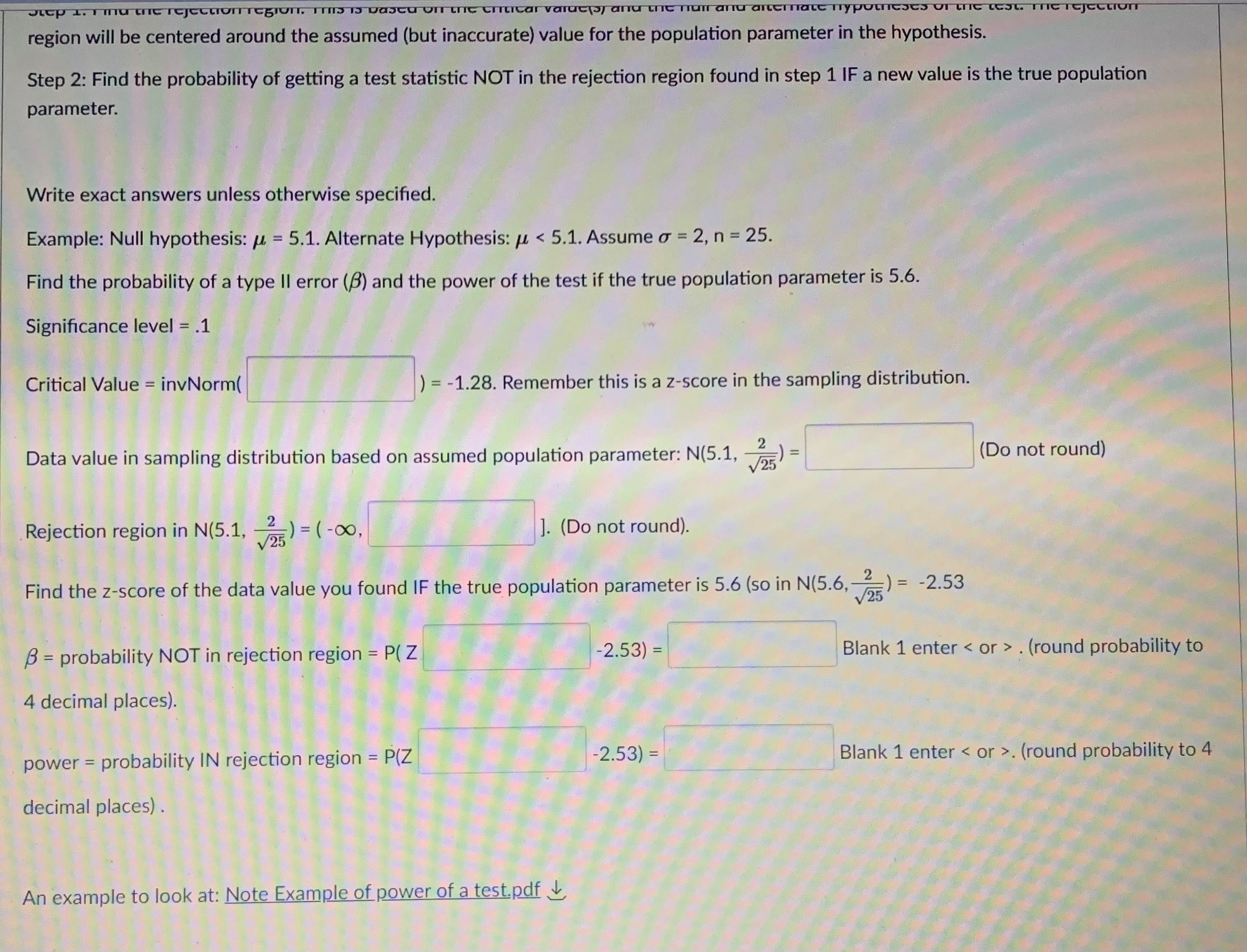
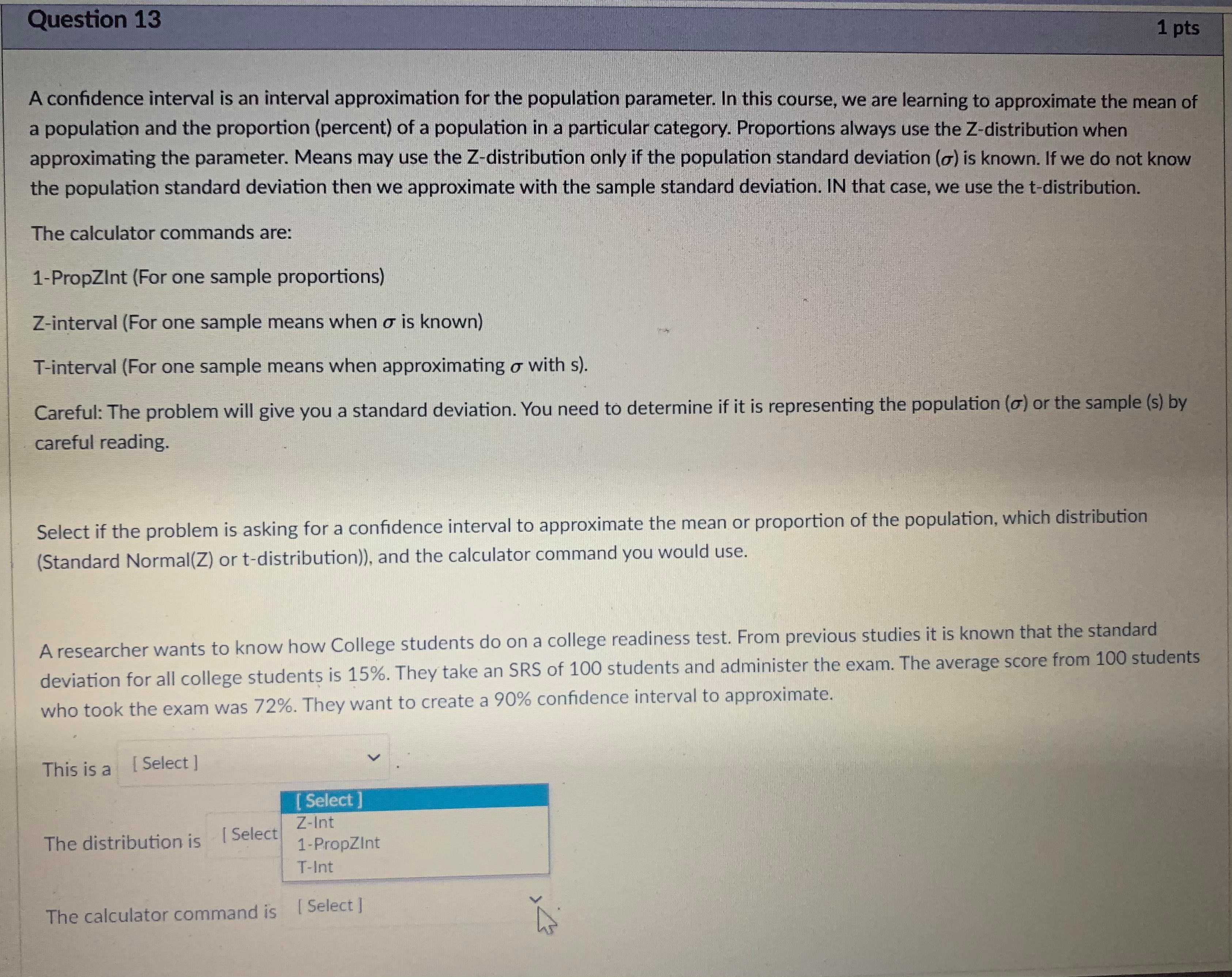
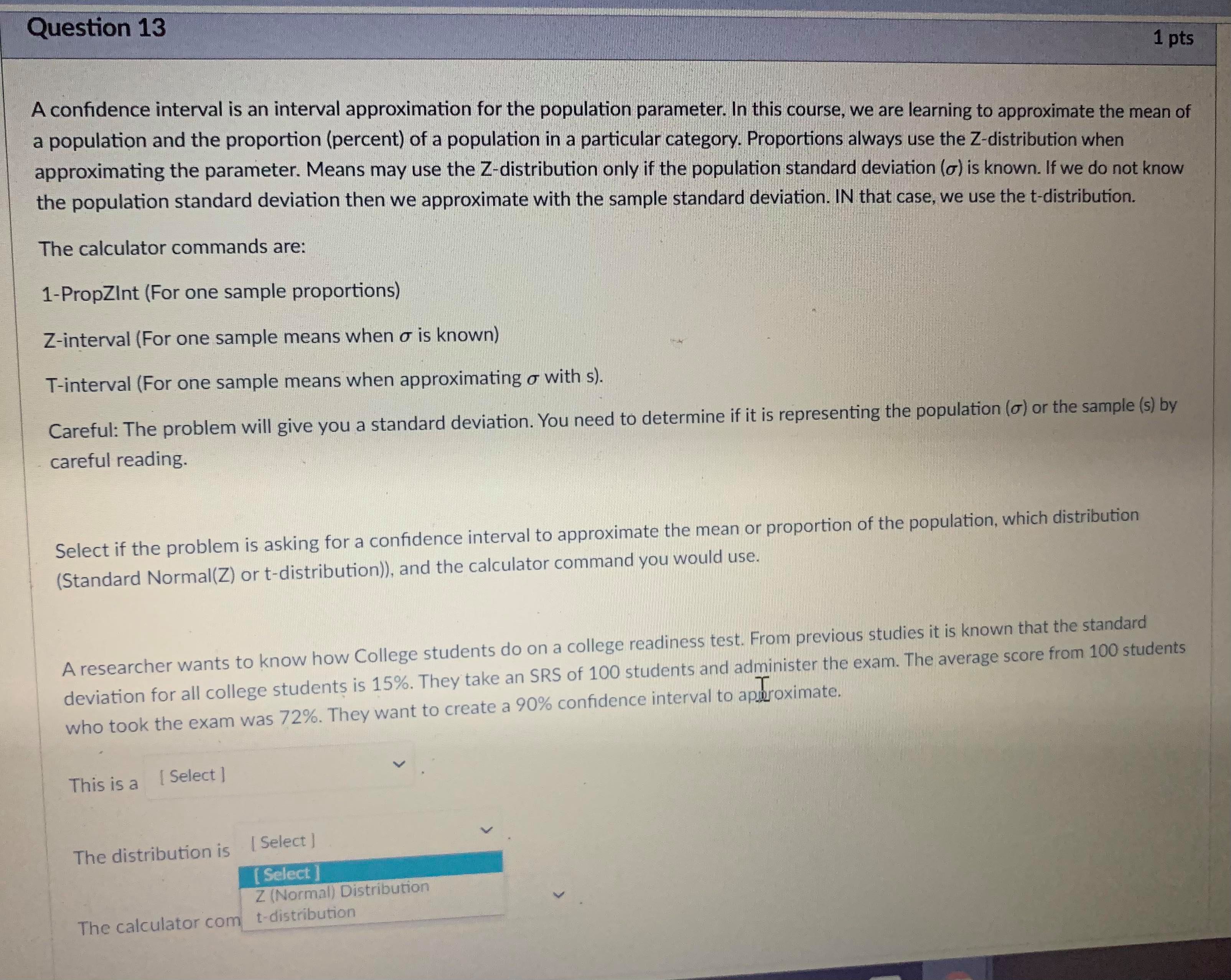
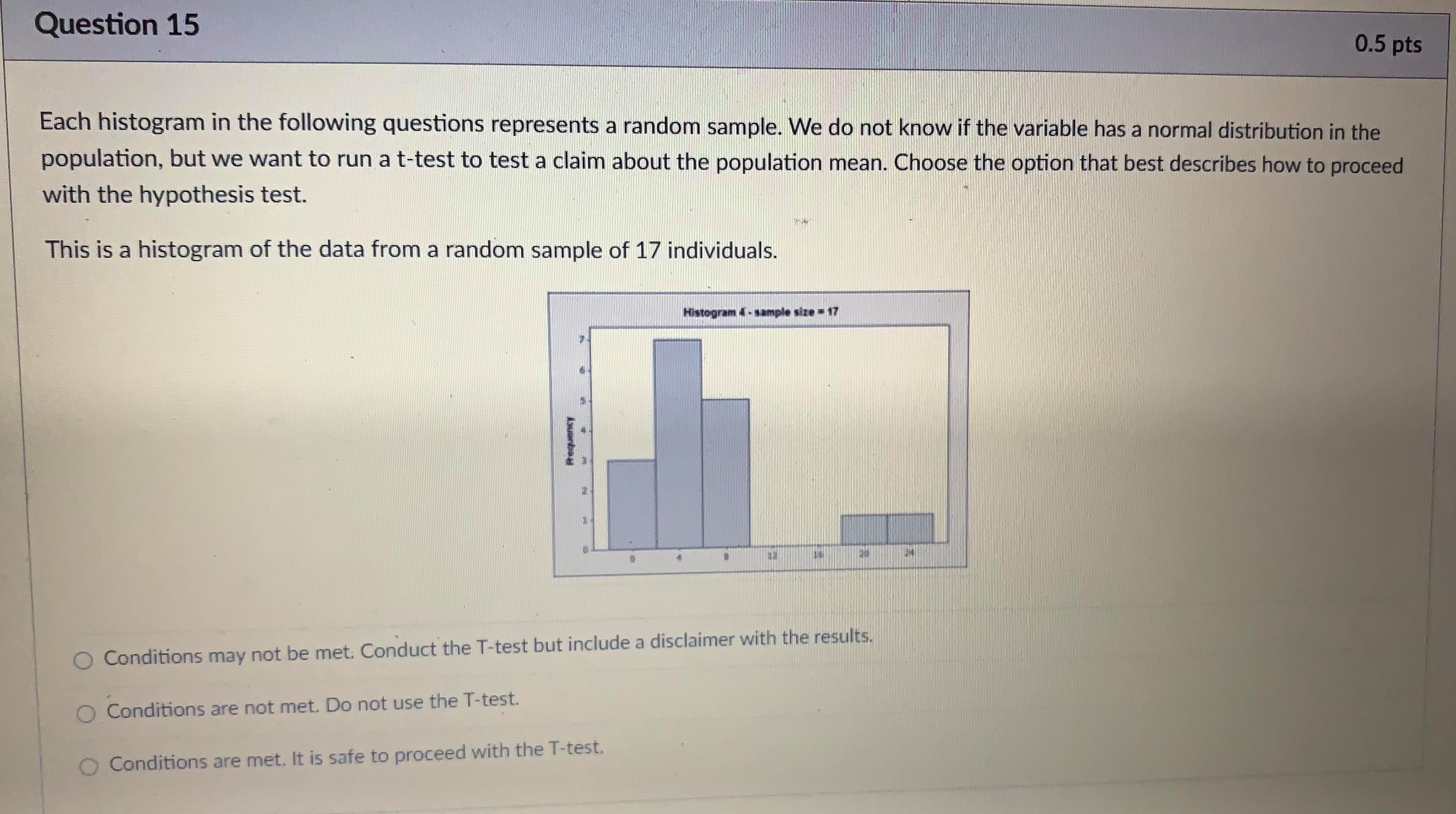
Question 5 1 pts A type II error is when you fail to reject the null hypothesis, but the null hypothesis is actually not true. The probability of making a type II error is called B. The power of a test is 1 - B. The power of a test tells you the probability that you did not make a type II error. You want B to be as close to O as possible and the power to be as close to 1 as possible. Both B and the power of a test depend on what the true population parameter is. B can be found by finding the probability that the test statistic is NOT in the rejection region if the true population parameter is equal to a specified value. Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / > 5.1. Assume o = 2, n = 25. Find the probability of a type II error (8) and the power of the test if the true population parameter is 5.6. Significance level = .05. Critical Value = invNorm(0.95) = I Remember this is a z-score in the sampling distribution. Round to 2 decimal places. Data value in sampling distribution based on assumed population parameter: N(5.1, -) = V25 Do not round) Rejection region in N(5.1, -2 V25) = [ oo). (Do not round) Find the z-score of the data value you found IF the true population parameter is 5.6 (so in N(5.6, -2 V25specmea value. Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / > 5.1. Assume o = 2, n = 25. Find the probability of a type II error (B) and the power of the test if the true population parameter is 5.6. Significance level = .05. Critical Value = invNorm(0.95) = Remember this is a z-score in the sampling distribution. Round to 2 decimal places. Data value in sampling distribution based on assumed population parameter: N(5.1, V25 Do not round) Rejection region in N(5.1, -) = [ oo). (Do not round) Find the z-score of the data value you found IF the true population parameter is 5.6 (so in N(5.6, -2 V25 B = probability NOT in rejection region = P( Z (round probability to 4 decimal places) .Question 6 1 pts A type II error is when you fail to reject the null hypothesis, but the null hypothesis is actually not true. The probability of making a type II error is called B. The power of a test is 1 - B. The power of a test tells you the probability that you did not make a type II error. You want B to be as close to O as possible and the power to be as close to 1 as possible. Both B and the power of a test depend on what the true population parameter is. B can be found by finding the probability that the test statistic is NOT in the rejection region if the true population parameter is equal to a specified value (which is different then the claim in the hypothesis). Step 1: Find the rejection region. This is based on the critical value(s) and the null and alternate hypotheses of the test. The rejection region will be centered around the assumed (but inaccurate) value for the population parameter in the hypothesis. Step 2: Find the probability of getting a test statistic NOT in the rejection region found in step 1 IF a new value is the true population parameter. Write exact answers unless otherwise specified. Example: Null hypothesis: / = 5.1. Alternate Hypothesis: / . (round probability to 4 decimal places). power = probability IN rejection region = P(Z -2.53) = Blank 1 enter . (round probability to 4 decimal places) . An example to look at: Note Example of power of a test.pdf &Question 13 1 pts A confidence interval is an interval approximation for the population parameter. In this course, we are learning to approximate the mean of a population and the proportion (percent) of a population in a particular category. Proportions always use the Z-distribution when approximationg the parameter. Means may use the Z-distribution only if the population standard deviation (o) is known. If we do not know the population standard deviation then we approximate with the sample standard deviation. IN that case, we use the t-distribution. The calculator commands are: 1-PropZint (For one sample proportions) Z-interval (For one sample means when o is known) T-interval (For one sample means when approximationg o with s). Careful: The problem will give you a standard deviation. You need to determine if it is representing the population () or the sample (s) by careful reading. Select if the problem is asking for a confidence interval to approximate the mean or proportion of the population, which distribution (Standard Normal(Z) or t-distribution)), and the calculator command you would use. A researcher wants to know how College students do on a college readiness test. From previous studies it is known that the standard deviation for all college students is 15%. They take an SRS of 100 students and administer the exam. The average score from 100 students who took the exam was 72%. They want to create a 90% confidence interval to approximate. This is a [ Select ] [ Select Z-Int The distribution is [ Select 1-PropZInt T-Int The calculator command is [ Select ]Question 13 1 pts A confidence interval is an interval approximation for the population parameter. In this course, we are learning to approximate the mean of a population and the proportion (percent) of a population in a particular category. Proportions always use the Z-distribution when approximationg the parameter. Means may use the Z-distribution only if the population standard deviation (o) is known. If we do not know the population standard deviation then we approximate with the sample standard deviation. IN that case, we use the t-distribution. The calculator commands are: 1-PropZInt (For one sample proportions) Z-interval (For one sample means when o is known) T-interval (For one sample means when approximationg o with s). Careful: The problem will give you a standard deviation. You need to determine if it is representing the population (o) or the sample (s) by careful reading. Select if the problem is asking for a confidence interval to approximate the mean or proportion of the population, which distribution (Standard Normal(Z) or t-distribution)), and the calculator command you would use. A researcher wants to know how College students do on a college readiness test. From previous studies it is known that the standard deviation for all college students is 15%. They take an SRS of 100 students and administer the exam. The average score from 100 students who took the exam was 72%. They want to create a 90% confidence interval to approximate. This is a [ Select ] The distribution is [Select ] [ Select Z (Normal) Distribution The calculator com t-distributionQuestion 13 1 pts A confidence interval is an interval approximation for the population parameter. In this course, we are learning to approximate the mean of a population and the proportion (percent) of a population in a particular category. Proportions always use the Z-distribution when approximationg the parameter. Means may use the Z-distribution only if the population standard deviation (o) is known. If we do not know the population standard deviation then we approximate with the sample standard deviation. IN that case, we use the t-distribution. The calculator commands are: 1-PropZInt (For one sample proportions) Z-interval (For one sample means when o is known) T-interval (For one sample means when approximationg o with s). Careful: The problem will give you a standard deviation. You need to determine if it is representing the population (o) or the sample (s) by careful reading. Select if the problem is asking for a confidence interval to approximate the mean or proportion of the population, which distribution (Standard Normal(Z) or t-distribution)), and the calculator command you would use. A researcher wants to know how College students do on a college readiness test. From previous studies it is known that the standard deviation for all college students is 15%. They take an SRS of 100 students and administer the exam. The average score from 100 students who took the exam was 72%. They want to create a 90% confidence interval to approximate. This is a [ Select ] [ Select] mean The distri proportion The calculator command is | Select ]Question 15 0.5 pts Each histogram in the following questions represents a random sample. We do not know if the variable has a normal distribution in the population, but we want to run a t-test to test a claim about the population mean. Choose the option that best describes how to proceed with the hypothesis test. This is a histogram of the data from a random sample of 17 individuals. Histogram & - sample size = 17 Requen Conditions may not be met. Conduct the T-test but include a disclaimer with the results. Conditions are not met. Do not use the T-test. Conditions are met. It is safe to proceed with the T-test