please help
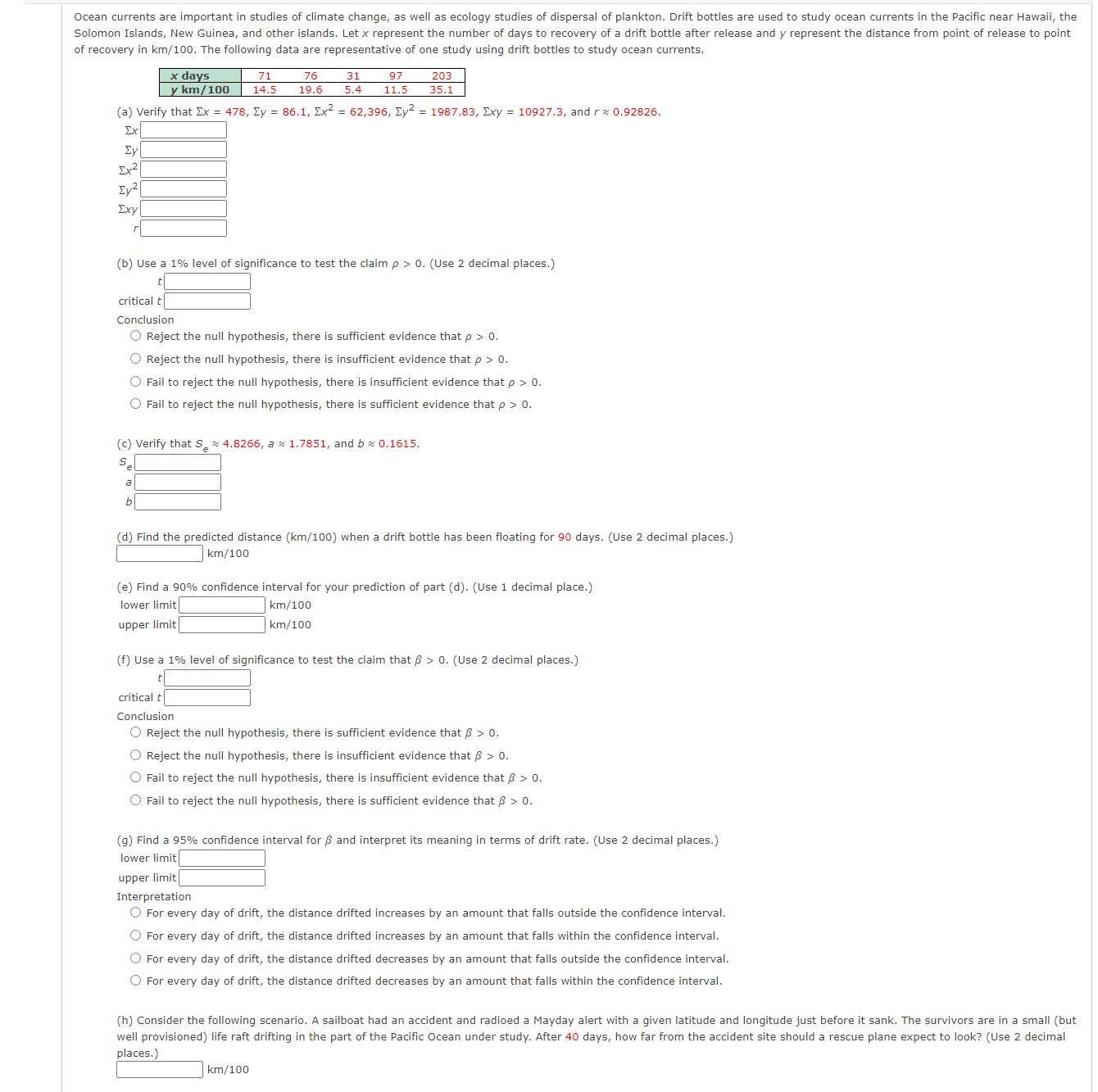
Ocean currents are important in studies of climate change, as well as ecology studies of dispersal of plankton. Drift bottles are used to study ocean currents in the Pacific near Hawaii, the Solomon Islands, New Guinea, and other islands. Let x represent the number of days to recovery of a drift bottle after release and y represent the distance from point of release to point of recovery in km/100. The following data are representative of one study using drift bottles to study ocean currents. * days y km / 100 14.5 19 .6 5.4 11.5 203 35.1 (a) Verify that Ex = 478, Ey = 86.1, Ex2 = 62,396, Zy2 = 1987.83, Exy = 10927.3, and / & 0.92826. Ex Ev Ex- SXV (b) Use a 1% level of significance to test the claim p > 0. (Use 2 decimal places.) critical t Conclusion O Reject the null hypothesis, there is sufficient evidence that p > 0. O Reject the null hypothesis, there is insufficient evidence that p > 0. Fail to reject the null hypothesis, there is insufficient evidence that p > 0. O Fail to reject the null hypothesis, there is sufficient evidence that p > 0. c) Verify that S. ~ 4.8266, a & 1.7851, and b & 0.1615. a b d) Find the predicted distance (km/100) when a drift bottle has been floating for 90 days. (Use 2 decimal places.) km/100 (e) Find a 90% confidence interval for your prediction of part (d). (Use 1 decimal place.) lower limit km/100 upper limit km/100 (f) Use a 1% level of significance to test the claim that B > 0. (Use 2 decimal places.) critical t Conclusion O Reject the null hypothesis, there is sufficient evidence that B > 0. O Reject the null hypothesis, there is insufficient evidence that B > 0. O Fail to reject the null hypothesis, there is insufficient evidence that B > 0. O Fail to reject the null hypothesis, there is sufficient evidence that B > 0. (g) Find a 95% confidence interval for B and interpret its meaning in terms of drift rate. (Use 2 decimal places.) lower limit upper limit Interpretation O For every day of drift, the distance drifted increases by an amount that falls outside the confidence interval. O For every day of drift, the distance drifted increases by an amount that falls within the confidence interval. O For every day of drift, the distance drifted decreases by an amount that falls outside the confidence interval. O For every day of drift, the distance drifted decreases by an amount that falls within the confidence interval. (h) Consider the following scenario. A sailboat had an accident and radioed a Mayday alert with a given latitude and longitude just before it sank. The survivors are in a small (but well provisioned) life raft drifting in the part of the Pacific Ocean under study. After 40 days, how far from the accident site should a rescue plane expect to look? (Use 2 decimal places. km/100