please help

thanks

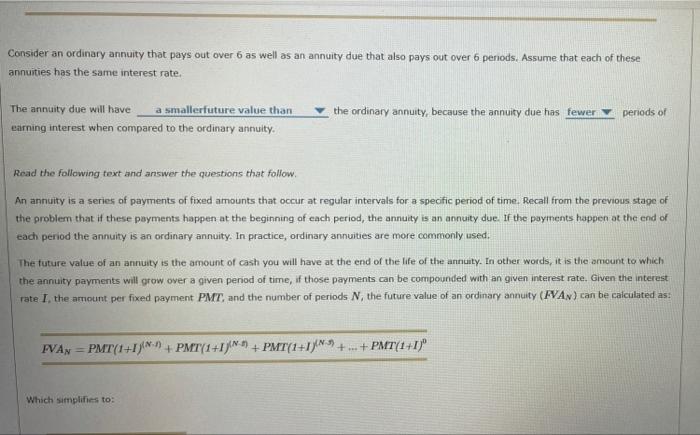
The future value of an annuity is a fundamental concept in finance. However, there are some details and distinctions that can make a big difference in the future value of an annuity. Watch the video and answer the question that follows. Consider an ordinary annuity that pays out over 6 as well as an annuity due that also pays out over 6 penods. Assume that each of these annuities has the same interest rate. The annuity due will have the ordinary annuity, because the annuity due has periods of earning interest when compared to the ordinary annulty. Read the following fext and answer the questions that follow. An annuity is a series of payments of fixed amounts that occur at regular intervals for a specific period of time. Recall from the previous stape of the problem that if these payments happen at the beginning of each period, the annuity is an annuity due. If the payments happen at the end of each period the annuity is an ordinary annuity. In practice, ordinary annuities are more commonly used. The future value of an annuity is the amount of cash you will have at the end of the life of the annuity. In other words, it is the amount to which the annuity payments will grow over a given period of time, if those payments can be compounded with an given interest rate. Given the interest rate I, the armount per fixed payment PMT, and the number of periods N, the future value of an ordinary annuity (FVA. FVAN=PMT(t+I)(NA)+PMT(1+I)(N1)+PMTT(1+I)(NT)++PMTT(1+I)0 Which simplifiess to: FVAN=PMT(1(1+I)N1) While in practice this calculation is typically done on a financial calculator or spreadsheet application, this equation can be useful when solving aninuity problems without those resources. When using a financial calculator to solve for the future value of an ordinary annuity, it is important to keep in mind the following: - The DW (present value) is the amount of funds at the start. For an ordinary annuity in isolation, this will be 0 . - The PMT is entered as a negative number when it is a cash outflow. - The I/YR is entered as a number, such as 10 for 10 percent, not as a decimal such as 0.10 for 10 percent. Note that financial calculators typically calculate the future value of an ordinary annuity by default, but can easily be adjusted to calculare the future value of an annusty due as well. A financal calculator can also be used to calculate the other components of an annuity, given all the values of the other components. For example, given the PV, IPRR, N, and FV, a financial calculator can solve for the period payment PMT. True or False: PMT is always entered as a positive number on a financial calculator when solving annuity problems.: Note that financal calculators typically calculate the future value of an ordinary annuity by default, but can casily be adjusted to calculate the future value of an annuity due as well. A financial calculator can also be used to calculate the other components of an annuity, given all the values of the other components. For example, given the PV, I/YR, N, and FV, a financial calculator can solve for the period payment PMT. True or False: PMT is always entered as a positive number on a financial calculator when solving annuity problems. True False Suppose you know want to solve for the fV of an ordinary annuity using a financial calculator. In order to solve for the FV of an ordinary annuity, which of the following components will you need to know the value of? Check all that apply? PMT N PV INRR Using a financial calculator is a common way of finding the future value of an ordinary annuity. Watch the video and then answer the questions that follow. Suppose that Kenji is 40 years old and has no retirement savings. He wants to begin saving for retirement, with the first payment coming one year from now. He can save $20,000 per year and will invest that amount in the stock market, where it is expected to yield an average annual return of 5.00% return. Assume that this rate will be constant for the rest of his's life. In short, this scenario fits all the criteria of an ordinary annuity Kenji would like to calculate how much money he will have at age 65. Use the folfowing table to indicate which values you should enter on your financial calculator. For example, if you are using the value of 1 for N, use the selection list above N in the table to select that value. Using a financial calculator yields a future value of this ordinary annuity to be approximately at age 65. Kenil would now like to calculate how much money he will have at age. 70 . Using a financial calculotor yiekls a future value of this ordinary annuity to be approximately at age 65. Kenji would now like to calculate how much money he will have at age 70 . Use the following table to indicate which values you should enter on your financial calculator. For example, if you are using the value of 1 for N, use the selection list above N in the table to relect that value, Using a financial calculator yields a future value of this ordieary annuity to be approximately at ape 70 Kenji expects to live for another 25 years of he retites at age 65 , with the same expected percent retum on investments in the stock market. He would like to calculate how much he can withdraw at the end of each year after retirement: Use the following table to indicate which values you should enter on your financial calculator in order to solve for pMT in this scenaria. For example, if you are using the value of 1 for N, use the selection list above N in the table to select that value. Using a financial calculatot, you can calculote that Kenj can withdraw at the end of each year atter retirement (assuming) tetirement at age 65), assuming a fixed withdrawal each year and 50 remaining at the end of his life. Kenj expects to live for another 20 years if he retires at age 70 , with the same expected percent return on investments in the stock market. Use the following table to indicate which values you should enter on your financial calculator. For example, if you are wang the value of 1 for N, use the selection lest above N in the table to select that value. Using a financial calculatot, you can calculate that Keny can withdraw at the end of each year atter retirement at age 70 , assuming a fored withdrawal each year and 50 remaining at the end of his life. Now it's time for you to practice what you've leamed. Suppose that Kenji is 40 years old and has no retirement savings. He wants to begin saving for retirement, with the first payment coming one vear from now. He can save $12,000 per year and will invest that amount in the stock market, where it is expected to yield an average annual return of 15.00% return. Assume that this rate will be constant for the rest of his's life. Kenji would like to calculate how much money he will have at age 65. Using a financial calculator yinlds a future value of this ordinary annuity to be approximately at age 65. Kenji would now like to calculate how much money he will have at age 70 . Using a financal calculator yelds a future value of this ordinary annuity to be approxmately at age 70 . Kenif expects to live for another 25 years if he retires at age 65 , with the- same expected percent return on investments in the stock market. Using a financial calculator, you can calculate that Kenji can withdraw at the end of each year after retirement (assuming) retirement at age 65 ), assuming a foxed withdrawal each year and $0 remaining at the end of his Me. Keris expects to live for another 20 yeais if he retires at age 70, with the same expected percent return on investments in the stock market. Ueing a financial calculator, you cin calculate that Kenji can withidraw of the end of each vear after retirement at age 70, assuming a fixed withdrawal each year and $0 remaining at the end of his lfe