please help to solve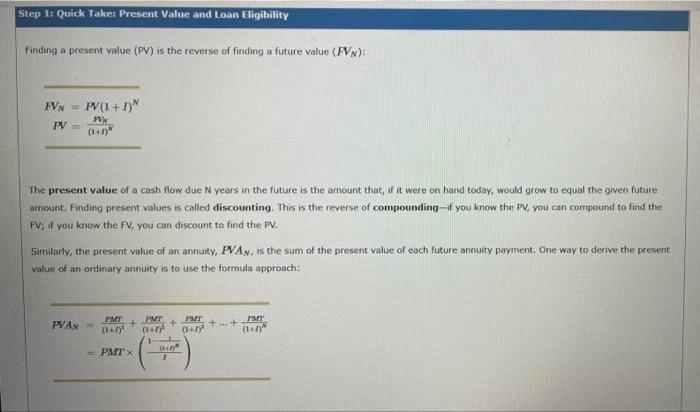

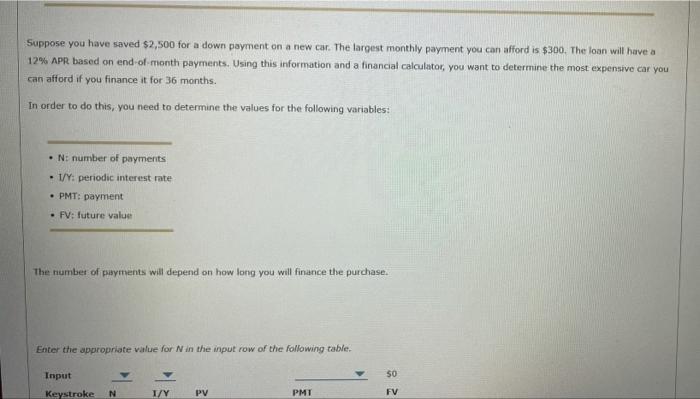
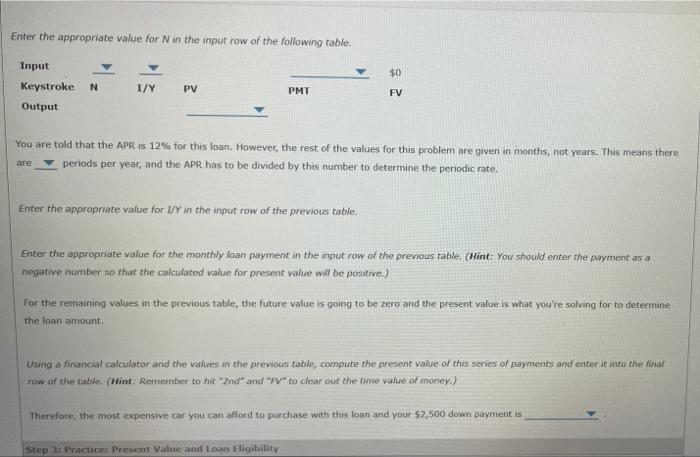
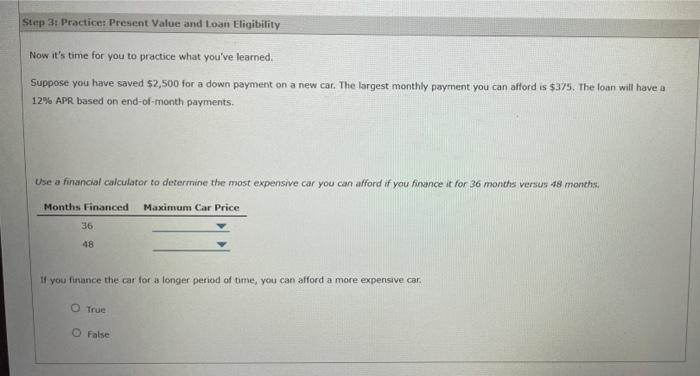
Finding a present value (PV) is the reverse of finding a future value (FVN) : FVNPV=PV(1+I)N=(1+T)NNN The present value of a cash flow due N years in the future is the amount that, if it were on hand today, would grow to equal the given future amount. Finding present values is called discounting. This is the reverse of compounding-if you know the PV, you can compound to find the FV; if you know the FV, you can discount to find the PV. Simitarly, the present value of an annuity, PVAN, is the sum of the present value of each future annuity payment, One way to derive the present value of an ordirtary annuity is to use the formula approach: PVAN=(1+n2PMr+(1+n2BMR+(1+n3PMr++(1+nNPMr =PMF(t1(1+p81) Another option is to find PVAN using a financial calculator, For example, suppose you want to find the present value of three annuity payments of $100 and an interest rate of 5%. In this case, the number of periods (N) is 3 , the interest rate (1/Y) is 5%, the payment (PMT) is $100, and the future value (FV) is 50 . Now you are ready to use your calculator to find the PVAN by entering values for N, IN, PMT, and FV and then pressing the PV key. (Note: Make sure your calculator is set to END mode.) In this case, the present value of this ordinary annuity is $272.32. If you know the present value (PV), you can discount it to find the future value (PV). True Fatse Step 2t Learnt Present Value and Loan Eligibifity True Fatse Step 2: tearn Present Value and toan Eligibility Calculating the present value of a series of future payments can often be heloful in determining your budget for a large purchase such as a car or house. Watch the following video for an example, then answer the questions that follow. Suppose you have saved $2,500 for a down payment on a new car. The largest monthly payment you can afford is $300. The loan will have a 12% APR based on end-of-month payments. Using this information and a financial calculator, you want to determine the most expensive car you can afford if you finance it for 36 months. In order to do this, you need to determine the values for the following variables: - N: number of payments - I/Y: periodic interest rate - PMT: payment - FV: future value The number of payments will depend on how long you will finance the purchase. Enter the appropriate value for N in the input row of the following table. Input PMI50FV Enter the appropriate value for N in the input row of the following table. You are told that the APR is 12% for this loan. However, the rest of the values for this problem are given in months, not years. This means there are periods per year, and the APR has to be divided by this number to determine the periodic rate. Enter the appropriate value for I/Y in the input row of the previous table. Enter the appropnate value for the monthly loan payment in the imput raw of the previous table. (Hint: You should enter the payment as a negative number so that the calculated value for present value will be positive). For the remaining values in the previous table, the future value is going to be zero and the present value is what you'te solving for to determine the loan amount. Using a financial calculator and the values in the previous table, compute the present value of this series of payments and enter it into the final row af the table. (Hint: Remember to hit "2nd" and "PV" to clear out the time value of money.) Therefore, the most expensive car you can afford to purchase with this loan and your $2,500 down payment is Now it's time for you to practice what you've learned. Suppose you have saved $2,500 for a down payment on a new car. The largest-monthly payment you can afford is $375. The loan will have a 12% APR based on end-of-month payments. Use a financial calculator to determine the most expensive car you can afford if you finance it for 36 months versus 48 months: If you finance the car lor a longer period of time, you can afford a more expensive car. True Fatse: Finding a present value (PV) is the reverse of finding a future value (FVN) : FVNPV=PV(1+I)N=(1+T)NNN The present value of a cash flow due N years in the future is the amount that, if it were on hand today, would grow to equal the given future amount. Finding present values is called discounting. This is the reverse of compounding-if you know the PV, you can compound to find the FV; if you know the FV, you can discount to find the PV. Simitarly, the present value of an annuity, PVAN, is the sum of the present value of each future annuity payment, One way to derive the present value of an ordirtary annuity is to use the formula approach: PVAN=(1+n2PMr+(1+n2BMR+(1+n3PMr++(1+nNPMr =PMF(t1(1+p81) Another option is to find PVAN using a financial calculator, For example, suppose you want to find the present value of three annuity payments of $100 and an interest rate of 5%. In this case, the number of periods (N) is 3 , the interest rate (1/Y) is 5%, the payment (PMT) is $100, and the future value (FV) is 50 . Now you are ready to use your calculator to find the PVAN by entering values for N, IN, PMT, and FV and then pressing the PV key. (Note: Make sure your calculator is set to END mode.) In this case, the present value of this ordinary annuity is $272.32. If you know the present value (PV), you can discount it to find the future value (PV). True Fatse Step 2t Learnt Present Value and Loan Eligibifity True Fatse Step 2: tearn Present Value and toan Eligibility Calculating the present value of a series of future payments can often be heloful in determining your budget for a large purchase such as a car or house. Watch the following video for an example, then answer the questions that follow. Suppose you have saved $2,500 for a down payment on a new car. The largest monthly payment you can afford is $300. The loan will have a 12% APR based on end-of-month payments. Using this information and a financial calculator, you want to determine the most expensive car you can afford if you finance it for 36 months. In order to do this, you need to determine the values for the following variables: - N: number of payments - I/Y: periodic interest rate - PMT: payment - FV: future value The number of payments will depend on how long you will finance the purchase. Enter the appropriate value for N in the input row of the following table. Input PMI50FV Enter the appropriate value for N in the input row of the following table. You are told that the APR is 12% for this loan. However, the rest of the values for this problem are given in months, not years. This means there are periods per year, and the APR has to be divided by this number to determine the periodic rate. Enter the appropriate value for I/Y in the input row of the previous table. Enter the appropnate value for the monthly loan payment in the imput raw of the previous table. (Hint: You should enter the payment as a negative number so that the calculated value for present value will be positive). For the remaining values in the previous table, the future value is going to be zero and the present value is what you'te solving for to determine the loan amount. Using a financial calculator and the values in the previous table, compute the present value of this series of payments and enter it into the final row af the table. (Hint: Remember to hit "2nd" and "PV" to clear out the time value of money.) Therefore, the most expensive car you can afford to purchase with this loan and your $2,500 down payment is Now it's time for you to practice what you've learned. Suppose you have saved $2,500 for a down payment on a new car. The largest-monthly payment you can afford is $375. The loan will have a 12% APR based on end-of-month payments. Use a financial calculator to determine the most expensive car you can afford if you finance it for 36 months versus 48 months: If you finance the car lor a longer period of time, you can afford a more expensive car. True Fatse