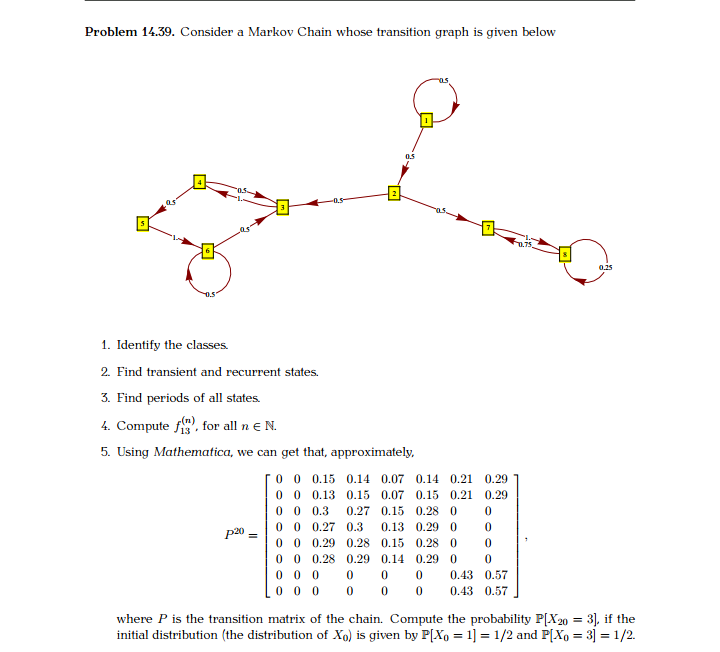
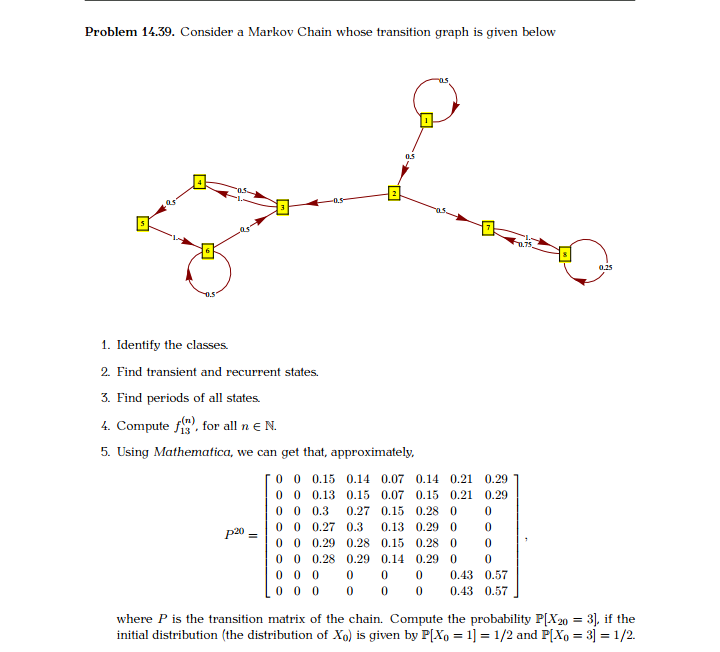
Please help tutors with my macro question

Problem 14.39. Consider a Markov Chain whose transition graph is given below -0.5 1. Identify the classes. 2. Find transient and recurrent states. 3. Find periods of all states. 4. Compute fis , fo " for all n e N. 5. Using Mathematica, we can get that, approximately, 0 0 0.15 0.14 0.07 0.14 0.21 0.29 0 0 0.13 0.15 0.07 0.15 0.21 0.29 0 0 0.3 0.27 0.15 0.28 0 p20 - 0 0 0.27 0.3 0.13 0.29 0 0 0 0 0.29 0.28 0.15 0.28 0 0 0 0 0.28 0.29 0.14 0.29 0 0 0 0 0 0.43 0.57 0 0 0.43 0.57 where P is the transition matrix of the chain. Compute the probability P[X20 = 3], if the initial distribution (the distribution of Xo) is given by P[Xo = 1] = 1/2 and P[Xo = 3] = 1/2.Problem 14.40. A country has m + 1 cities (me N), one of which is the capital. There is a direct railway connection between each city and the capital, but there are no tracks between any two "non-capital" cities. A traveler starts in the capital and takes a train to a randomly chosen non- capital city (all cities are equally likely to be chosen), spends a night there and returns the next morning and immediately boards the train to the next city according to the same rule, spends the night there, .... etc. We assume that his choice of the city is independent of the cities visited in the past. Let {X}ner, be the number of visited non-capital cities up to (and including) day n, so that Xo = 1, but X1 could be either 1 or 2, etc. 1. Explain why {X}men, is a Markov chain on the appropriate state space S and the find the transition probabilities of { X,)meN, ie,, write an expression for P[Xn+1 = j|Xn = 1], for i, je S. 2. Find recurrent and transient classes and periods of all states. Sketch the transition graph for m = 3. 3. Let Tm be the first time the traveler has visited all m non-capital cities, ie. Tm = min{n ( No : X, = m}. What is the distribution of 7m. for m = 1 and m = 2. 4. Compute E[m] for general me N. (Note: you don't need to use any heavy machinery. In particular, no knowledge of the "absorption and reward" techniques are necessary.)Problem 14.41. In a Markov chain with a finite number of states, the fundamental matrix is given by F = 3 4 The initial distribution of the chain is uniform on all transient states. The expected value of To = min {n ( No : Xn ( C}, where C denotes the set of all recurrent states is (a) 7 (b) 8 (c) 25 (d) (e) None of the above. Solution: The correct answer is (c). Using the reward g = 1, the vector v of expected values of To, where each entry corresponds to a different transient initial state is v=Fg =$4 4 -[$] Finally, the initial distribution puts equal probabilities on the two transient states, so, by the law of total probability, E[re] = } x 7 + ; x ! = . Problem 14.42. A fair 6-sided die is rolled repeatedly, and for n E N, the outcome of the n-th roll is denoted by Y, (it is assumed that {Ym}men are independent of each other). For n E No. let Xn be the remainder (taken in the set {0. 1, 2, 3, 4}) left after the sum ER_, Yx is divided by 5, i.e. Xo = 0, and Xn = YA ( mod 5), for n EN, A= 1 making {X,}men, a Markov chain on the state space {0, 1, 2,3,4) (no need to prove this fact). 1. Write down the transition matrix of the chain. 2. Classify the states, separate recurrent from transient ones, and compute the period of each state.*=0 Problem 14.43. In a "Gambler's ruin" situation with a = 3 (S = {0, 1, 2, 3}) and p = = compute the probability that the gambler will go bankrupt before her wealth reaches a, if her initial wealth is Xo = 2. You must use the matrix technique (the one in the "Absorption and Reward" lecture with U. Q. etc.) Remember that for a, b, c, de R with ad - be # 0, we have b c ad - beProblem 14.45. A math professor has 4 umbrellas. He keeps some of them at home and some in the office. Every morning, when he leaves home, he checks the weather and takes an umbrella with him if it rains. In case all the umbrellas are in the office, he gets wet. The same procedure is repeated in the afternoon when he leaves the office to go home. The professor lives in a tropical region, so the chance of rain in the afternoon is higher than in the morning; it is 1/5 in the afternoon and 1/20 in the morning. Whether it rains of not is independent of whether it rained the last time he checked. On day 0, there are 2 umbrellas at home, and 2 in the office. What is the expected number of days that will pass before the professor gets wet (remember, there are two trips each day)? What is the probability that the first time he gets wet it is on his way home from the office?Problem 14.49. An airline reservation system has two computers, only one of which is in opera- tion at any given time. A computer may break down on any given day with probability pe (0, 1). There is a single repair facility which takes two days to restore a computer to normal. The facilities are such that only one computer at a time can be dealt with. Form a Markov chain that models the situation (make sure to keep track of the number of machines in operation as well as the status of the machine - if there is one - at the repair facility). 1. Find the stationary distribution. 2. What percentage of time (on average) are no machines operable? 3. What percentage of time (on average) is exactly one machine operable?Problem 14.50. Let {Y, }men, be a sequence of die-rolls, i.e., a sequence of independent random variables with distribution 1 2 3 4 5 6 1/6 1/6 1/6 1/6 1/6 1/6 Let { X}meNo be a stochastic process defined by X, = max(Yo. Y1, .... Y,). In words, X, is the maximal value rolled so far. 1. Explain why X is a Markov chain, and find its transition matrix and the initial distribution. 2. Supposing that the first roll of the die was 3, i.e., Xo = 3, what is the expected time until a 6 is reached? 3. Under the same assumption as above (Xo = 3), what is the probability that a 5 will not be rolled before a 6 is rolled for the first time? 4. Starting with the first value Xo = 3, each time a die is rolled, the current record (the value of X ) is written down. When a 6 is rolled for the first time all the numbers are added up and the result is called S (the final 6 is not counted). What is the expected value of S? (Hints: 1. You can eliminate 1 and 2 from the state space for parts (2) and (3).) 2. Use the fact that rotr27 -r abc A- = when A = 0 h -r , for a, b, c,r > 0. 0 C