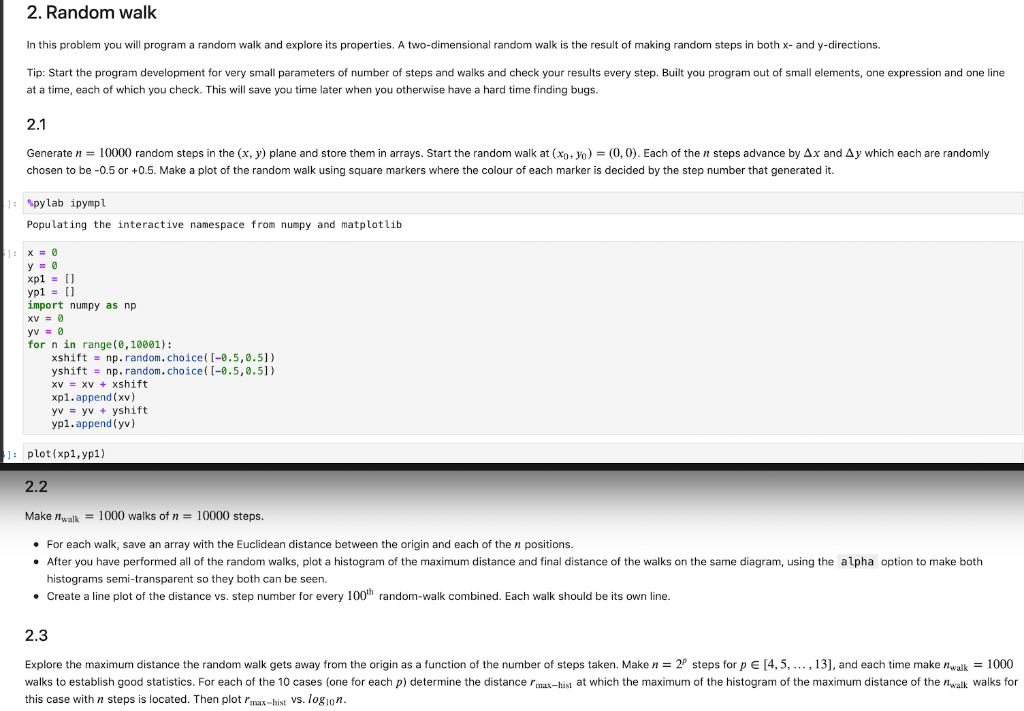
Please help with 2.2 and 2.3! I have provided the working code for 2.1 to work off of. Thank you!

2. Random walk In this problem you will program a random walk and explore its properties. A two-dimensional random walk is the result of making random steps in both X- and y-directions. Tip: Start the program development for very small parameters of number of steps and walks and check your results every step. Built you program out of small elements, one expression and one line at a time, each of which you check. This will save you time later when you otherwise have a hard time finding bugs. 2.1 Generate n = 10000 random steps in the (x, y) plane and store them in arrays. Start the random walk at (xo yo) = (0,0). Each of the n steps advance by Ax and Ay which each are randomly chosen to be -0.5 or +0.5. Make a plot of the random walk using square markers where the colour of each marker is decided by the step number that generated it. Spylab ipympl Populating the interactive namespace from numpy and matplotlib yo xp1 = [] yp1 = [] import numpy as np XVE y = 0 for n in range(0, 10001): xshift = np.random.choice((-0.5, 0.5]) yshift = np. random. choice((-0.5, 0.5)) XV = XV + xshift xpi.append(xv) yv = y + yshift ypi.append(y) ]: plot(xp1, yp1) 2.2 Make nwalk = 1000 walks of n = 10000 steps. For each walk, save an array with the Euclidean distance between the origin and each of the n positions. After you have performed all of the random walks, plot a histogram of the maximum distance and final distance of the walks on the same diagram, using the alpha option to make both histograms semi-transparent so they both can be seen. Create a line plot of the distance vs. step number for every 100 random-walk combined. Each walk should be its own line. 2.3 Explore the maximum distance the random walk gets away from the origin as a function of the number of steps taken. Make n = 2 steps for p (4,5,...,13), and each time make nwalk = 1000 walks to establish good statistics. For each of the 10 cases (one for each p) determine the distance Imax-hist at which the maximum of the histogram of the maximum distance of the nwalk walks for this case with n steps is located. Then plot Imax-hist vs. logion. 2. Random walk In this problem you will program a random walk and explore its properties. A two-dimensional random walk is the result of making random steps in both X- and y-directions. Tip: Start the program development for very small parameters of number of steps and walks and check your results every step. Built you program out of small elements, one expression and one line at a time, each of which you check. This will save you time later when you otherwise have a hard time finding bugs. 2.1 Generate n = 10000 random steps in the (x, y) plane and store them in arrays. Start the random walk at (xo yo) = (0,0). Each of the n steps advance by Ax and Ay which each are randomly chosen to be -0.5 or +0.5. Make a plot of the random walk using square markers where the colour of each marker is decided by the step number that generated it. Spylab ipympl Populating the interactive namespace from numpy and matplotlib yo xp1 = [] yp1 = [] import numpy as np XVE y = 0 for n in range(0, 10001): xshift = np.random.choice((-0.5, 0.5]) yshift = np. random. choice((-0.5, 0.5)) XV = XV + xshift xpi.append(xv) yv = y + yshift ypi.append(y) ]: plot(xp1, yp1) 2.2 Make nwalk = 1000 walks of n = 10000 steps. For each walk, save an array with the Euclidean distance between the origin and each of the n positions. After you have performed all of the random walks, plot a histogram of the maximum distance and final distance of the walks on the same diagram, using the alpha option to make both histograms semi-transparent so they both can be seen. Create a line plot of the distance vs. step number for every 100 random-walk combined. Each walk should be its own line. 2.3 Explore the maximum distance the random walk gets away from the origin as a function of the number of steps taken. Make n = 2 steps for p (4,5,...,13), and each time make nwalk = 1000 walks to establish good statistics. For each of the 10 cases (one for each p) determine the distance Imax-hist at which the maximum of the histogram of the maximum distance of the nwalk walks for this case with n steps is located. Then plot Imax-hist vs. logion