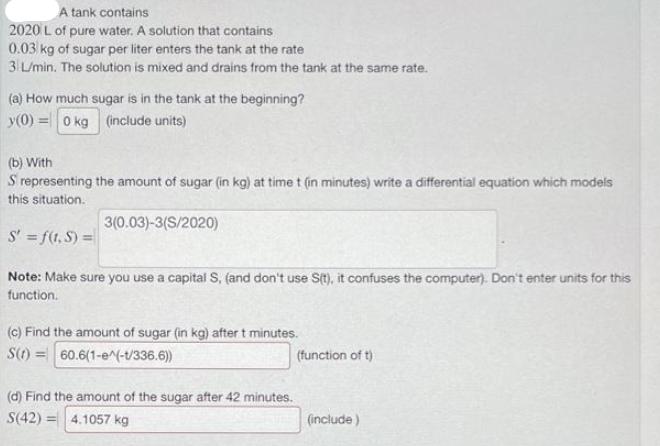
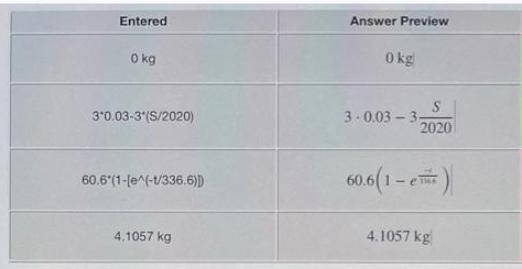
A tank contains 2020 L of pure water. A solution that contains 0.03 kg of sugar per liter enters the tank at the rate 3 L/min. The solution is mixed and drains from the tank at the same rate. (a) How much sugar is in the tank at the beginning? y(0) 0 kg (include units) = (b) With S representing the amount of sugar (in kg) at time t (in minutes) write a differential equation which models this situation. 3(0.03)-3(S/2020) S'=f(t, S) = Note: Make sure you use a capital S, (and don't use S(t), it confuses the computer). Don't enter units for this function. (c) Find the amount of sugar (in kg) after t minutes. S(t)= 60.6(1-e^(-1/336.6)) (d) Find the amount of the sugar after 42 minutes. S(42) 4.1057 kg (function of t) (include) Entered 0 kg 3*0.03-3*(S/2020) 60.6 (1-[e^(-1/336.6)D 4.1057 kg Answer Preview 0 kg S 2020 3-0.03-3- 60.6(1-) 4.1057 kg