please help with python3 code
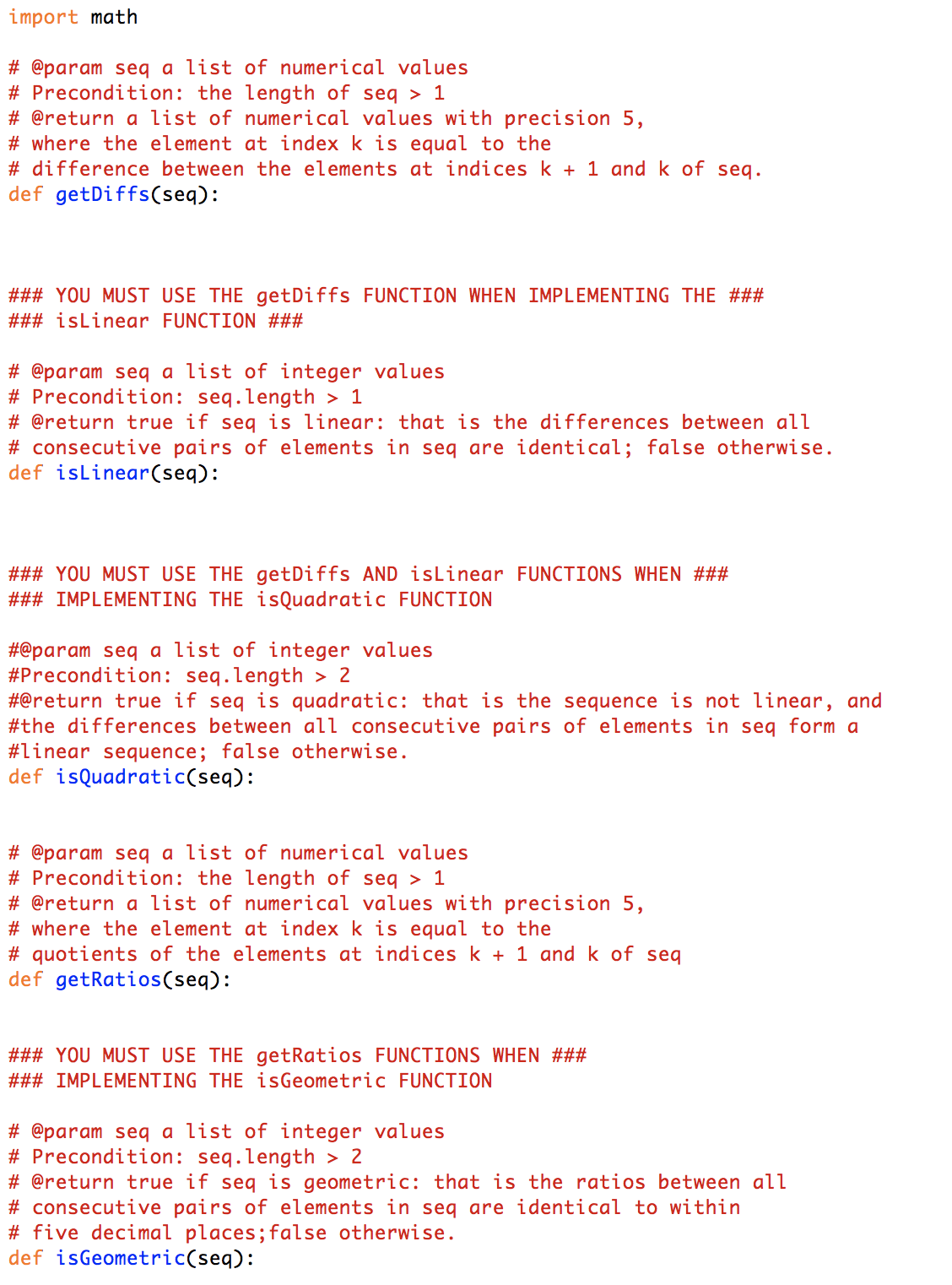
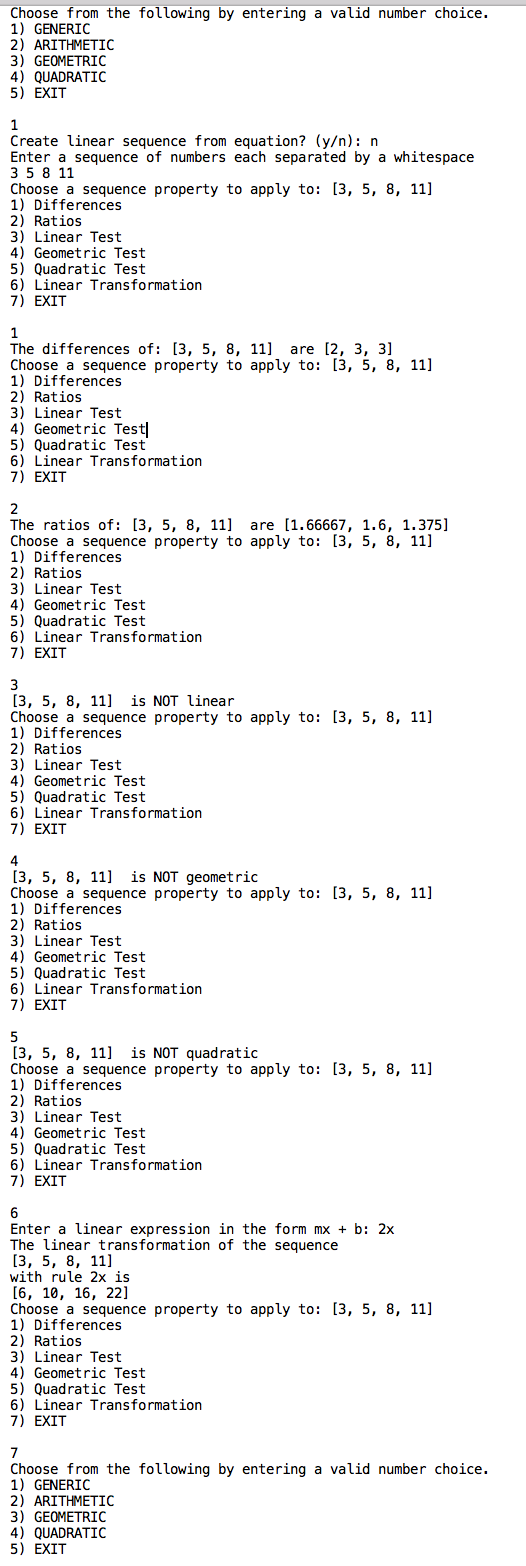
import math An arithmetic sequence, is a sequence of numbers such that the difference between consecutive terms is constant. This constant is referred to as the common difference. Any arithmetic sequence can be defined as a linear function of the form f(n) = a1 + (n1)d, where a1 is the first term, d is the common difference, and the domain n is the natural numbers {1,2,3,..} class Arithmetic: # initializer with default first_term = 1, default common_difference = 5 # and default max_terms = 10 def __init__(self, first_term = 1, common_difference = 5, max_terms = 10): self.first_term = first_term self.common_difference = common_difference self.max_terms = max_terms ****** COMPLETE THE METHOD BELOW @param mx_plus_b a string containing a linear expression of the form mx + b Precondition: mx_plus_b must be a valid linear expression in the form mx + b sets first_term and common_difference to the correct values based on the parameter mx_plus_b, default max terms = 5 ef reset(self, mx_plus_b = 'x', max_terms = 5): Qttt # ****** COMPLETE THE METHOD BELOW # returns the sequence as a list # @param none # @return a list containing the terms of the sequence rounded to # a precision of 6 def asList(self): A geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, nonzero number called the common ratio. Any geometric sequence can be defined as an exponential function of the form f(n) = a1(r)An, where a1 is the first term, r is the common ratio raised to the n power, and the domain n is the whole numbers {O,1,2,3,..} class Geometric: # initializer with default first_term = 1, default common_ratio = 2 # and default max_terms = 10 def __init__(self, first_term = 1, common_ratio = 2, max_terms = 10): self.first_term = first_term self.common_ratio = common_ratio self.max_terms = max_terms %%##k% # ****** COMPLETE THE METHOD BELOW # @param arn a string containing an exponential expression of the form # a(r)An or rAn, r > O, r not equal to 1, a not equal to O # Precondition: arn must be a valid exponential expression of the form # aCr)An or rAn, r > 0, r not equal to 1, a not equal to 0 # sets first_term and common_ratio to the correct values based on # the parameter arn, default exponential expression = ZAn # default max terms = 5 # @return void def reset(self, arn = 'ZAn', max_terms = 5): # ****** COMPLETE THE METHOD BELOW # returns the sequence as a list # @param none # @return a list containing the terms of the sequence rounded to # a precision of 6 def asList(self): # A quadratic sequence, is a sequence of numbers in which the second # differences between each consecutive term differ by the same amount, # called a common second difference. Any geometric sequence can be defined # as a quadratic function of the form f(n) = AnAZ + Bn + C, where A, B, and # C are constants, and nAZ means n raised to the 2nd power. class Quadratic: # initializer with default constants A = 1, B = O, C = O # and default max_terms = 10 def __init__(self, A = 1, B = 0, C = 0, max_terms = 10): self.A = A self.B = B self.C = C self.max_terms = max_terms # ****** COMPLETE THE METHOD BELOW # returns the sequence as a list # @param none # @return a list containing the terms of the sequence def asList(self): \fimport my_sequence # Create a default Arithmetic sequence object A1 = my_sequence . Arithmetic() # Create a default Geometric sequence object G1 = my_sequence . Geometric() # Create a default Quadratic sequence object Q1 = my_sequence . Quadratic() # Create a specific Quadratic sequence object Q2 = my_sequence . Quadratic(1, 1, 1,5) # test the aslist method for all sequence objects print(A1 . asList()) print(G1 . asList()) print(Q1. asList()) print(Q2 . asList()) # test the reset method for the Arithmetic sequence object Al . reset('1. 1x+1' ) print(A1 . asList()) # test the reset method for the Geometric sequence object G1 . reset('5(2.1)An' ) print(G1 . asList())import math # @param seq a list of numerical values # Precondition: the length of seq > 1 # @return a list of numerical values with precision 5, # where the element at index k is equal to the # difference between the elements at indices k + 1 and k of seq. def getDiffsCseq): ### YOU MUST USE THE getDiffs FUNCTION WHEN IMPLEMENTING THE ### ### isLinear FUNCTION ### # @param seq a list of integer values # Precondition: seq.length > 1 # @return true if seq is linear: that is the differences between all # consecutive pairs of elements in seq are identical; false otherwise. def isLinearCseq): ### YOU MUST USE THE getDiffs AND isLinear FUNCTIONS WHEN ### ### IMPLEMENTING THE isQuadratic FUNCTION #@param seq a list of integer values #Precondition: seq.length > 2 #@return true if seq is quadratic: that is the sequence is not linear, and #the differences between all consecutive pairs of elements in seq form a #linear sequence; false otherwise. def isQuadratic(seq): # @param seq a list of numerical values # Precondition: the length of seq > 1 # @return a list of numerical values with precision 5, # where the element at index k is equal to the # quotients of the elements at indices k + 1 and k of seq def getRatiosCseq): ### YOU MUST USE THE getRatios FUNCTIONS WHEN ### ### IMPLEMENTING THE isGeometric FUNCTION # @param seq a list of integer values # Precondition: seq.length > 2 # @return true if seq is geometric: that is the ratios between all # consecutive pairs of elements in seq are identical to within # five decimal places;false otherwise. def isGeometric(seq): # @param mx_plus_b a string containing a linear expression of the form # mx + b # Precondition: mx_plus_b must be a valid linear expression in the form mx + b # @return a list containing the slope m and vertical intercept b # both as float values. The slope should be stored in the list first # followed by the vertical intercept def getLinearParameters(mx_plus_b) : ### YOU MUST USE THE getLinearParameters FUNCTION WHEN ### ### IMPLEMENTING THE LinearTransformation FUNCTION # @params seq a list of numerical values, mx_plus_b a string containing # a linear expression of the form mx + b # Preconditions: the length of seq > 1, mx_plus_b must be a valid # linear expression in the form mx + b # @return a list containing values generated by multiplying each element # of seq by the slope m followed by adding the vertical intercept b. # For example, if seq = [2, 4, 8, 16], and mx_plus_b = "3x-4", then the # return list would be [2, 8, 20, 44] def linearTransformation(seq, mx_plus_b) : ### YOU MUST USE THE getLinearParameters FUNCTION WHEN ### ### IMPLEMENTING THE LinearSequence FUNCTION # @params num_terms the number of terms to generate, mx_plus_b a # string containing a linear expression of the form mx + b # Preconditions: num_terms > 1, mx_plus_b must be a valid # linear expression in the form mx + b # @return a list containing the terms of the linear sequence def linearSequence(num_terms, mx_plus_b) : # @param seq a list of numerical values that form a linear sequence # Precondition: seq . length > 1 # @return a string in the form mx + b that defines the linear sequence # For example, if seq = [3, 8, 13, 18], then the function would # return "5x-2" def getLinearEquation(seq) :1) GENERIC Choose from the following by entering a valid number choice. ARITHMETIC GEOMETRIC 4) QUADRATIC 5) EXIT Create linear sequence from equation? (y) : n Enter a sequence of numbers each separated by a whitespace 3 5 8 11 Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences Ratios Linear Test Geometric Test Quadratic Test 7) EXIT Linear Transformation 1 The differences of: [3, 5, 8, 11] are [2, 3, 3] Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test| 5) Quadratic Test 6) Linear Transformation 7) EXIT 2 The ratios of: [3, 5, 8, 11] are [1. 66667, 1.6, 1.375] Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences 2) Ratios 3) Linear Test Geometric Test Quadratic Test Linear Transformation 7) EXIT 3 [3, 5, 8, 11] is NOT linear Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences Ratios Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 4 [3, 5, 8, 11] is NOT geometric Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences Ratios Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 5 [3, 5, 8, 11] is NOT quadratic Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences Ratios Linear Test Geometric Test Quadratic Test Linear Transformation 7) EXIT 6 Enter a linear expression in the form mx + b: 2x The linear transformation of the sequence [3, 5, 8, 11] with rule 2x is [6, 10, 16, 22] Choose a sequence property to apply to: [3, 5, 8, 11] 1) Differences Ratios Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT Choose from the following by entering a valid number choice. 1) GENERIC ARITHMETIC GEOMETRIC QUADRATIC 5) EXIT1 Create linear sequence from equation? (yin): y Enter the number of terms for this sequence: 5 Enter a linear expression in the form mx + b: 2x+3 Choose a sequence property to apply to: [1.8, 1.8, 3.8, 5.8, 7.81 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 7 Choose from the following by entering a valid number choice. 1) GENERIC 2) ARITHMETIC 3) GEQMETRIC 4) QUADRATIC 5) EXIT 2 Enter a linear expression in the form mx + b: x Enter the number of terms for this sequence: 4 Choose a sequence property to apply to: [1, 2, 3, 4] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 1) EXIT 7 Choose from the following by entering a valid number choice. 1) GENERIC 2) ARITTMETIC 3) GEDMETRIC 4) DUADRATIC 5) EXIT 3 Enter an gxpgntgal expression in the form r\"n or aIr)'n: 2'n Enter the number of terms for this sequence: 5 Choose a sequence property to apply to: [1, 2, 4, B, 16] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 4 [1: -2, 4, 8, 16] is geometric Choose a sequence property to apply to: [1, 2, 4, B, 16] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 6 Enter a linear expression in the form mx + b: 3x+1 The linear transformation of the sequence [1, 2, 4, 8, 16] with rule 3x+1 is [4, 7, 13, 25, 49] Choose a sequence property to apply to: [1, 2, 4, 8, 16] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 7 Choose from the following by entering a valid number choice. 1) GENERIC 2) ARITTMETIC 3) GEDMETRIC 4) QUADRATIC 5) EXIT 4 Enter the parameters A, B, and C each seperated by whitespace: 1 71 3 Enter the number of terms for this sequence: Choose a sequence property to apply to: [3.3, 5.3, 9.0] 1) Differences 2) Ratios 3) Linear Test 4) Geometric Test 5) Quadratic Test 6) Linear Transformation 7) EXIT 7 Choose from the following by entering a valid number choice. 1) GENERIC 2) ARITTMETIC 3) GEDMETRIC 4) QUADRATIC .5) EXIT
