Please help with these questions:

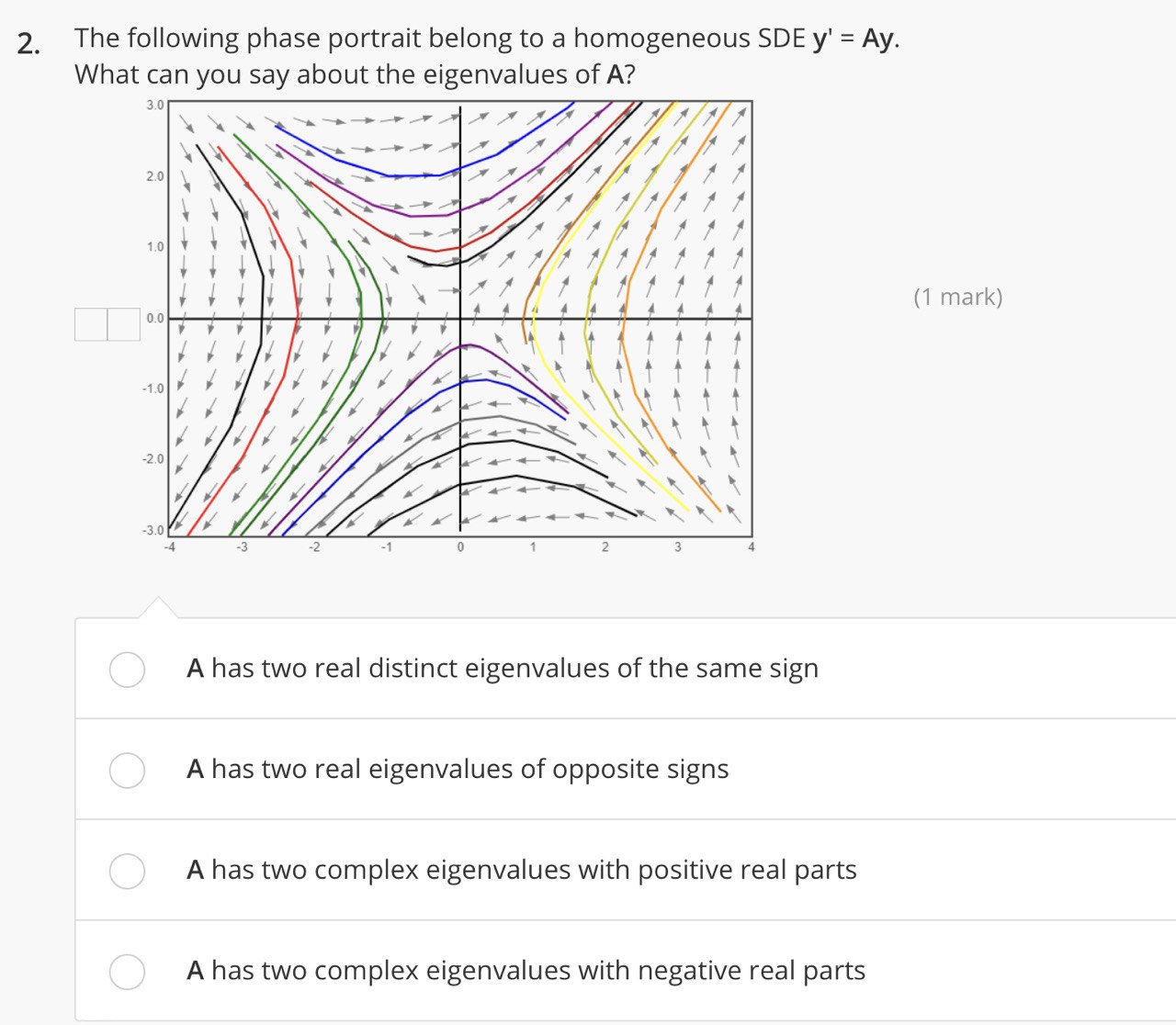
1 _5 The underlying matrix of a homogeneous SDE is given by ( l ) . Determine the type and stability of its equilibrium point. (1 mark) Node; asymptotically stable Node: unstable Spiral point; asymptotically stable Spiral point; unstable Saddle point: unstable Saddle paint; stable 3. A particular solution of a homogeneous SDE is given by y1 = 2etcos(t) - 3etsin(t) y2 = -2etsin(t) - 3etcos(t). (1 mark) Which of the following is the correct type of equilibrium point of the system? O Center O Node O Spiral point Saddle point O Degenerate node5. The underlying 2x2 matrix A of a system y' = Ay is non-diagonalizable. Suppose r is the only eigenvalue of A, v is an eigenvector of A and u is a generalized eigenvector of A corresponding to v. (1 mark) Which of the first four statements below is correct? (If all of them are incorrect, choose the last option) O The generalized eigenvector u is a solution of the system (rl - A) u = v. O The general solution of y' = Ay is given by civtert + Czuert. O The wronskian of vtet and uett is not zero for any non-zero value t. We cannot find two linearly independent solutions for y' = Ay. O None of the above.The following phase portrait belong to a homogeneous SDE y' = Ay. What can you say about the eigenvalues of A? (\"I mark) A has two real distinct eigenvalues of the same sign A has two real eigenvalues of opposite signs A has two complex eigenvalues with positive real parts A has two complex eigenvalues with negative real parts Which of the following first four statements is not true about the homogeneous SDE with the following phase portrait? if the statements are all true, select the last option. (The trajectories above the red lines are moving "upwards"; and the trajectories below the red line are moving "downwards") l'i/l 0 is one of the eigenvalues ofthe underlying matrix of this SDE. All the points along the red line are equilibrium points for this SDE. The trajectories of the phase portraits are all the parallel lines in black together with the red line. There is an eigenvector of the underlying matrix that is parallel to the red line All the above are true